Analytisk hierarkisk process

En enkel AHP-hierarki, med slutliga prioriteringar. Målet är att välja den mest lämpliga ledaren från ett fält med tre kandidater. De faktorer som ska beaktas är erfarenhet, utbildning, karisma och ålder. Enligt beslutsfattarnas bedömningar är Dick den starkaste kandidaten, följt av Tom, sedan Harry. Deras beslutsprocess beskrivs ingående i en bilaga till denna artikel .

I teorin om beslutsfattande är den analytiska hierarkiprocessen ( AHP ), även analytisk hierarkiprocess , en strukturerad teknik för att organisera och analysera komplexa beslut , baserade på matematik och psykologi . Den utvecklades av Thomas L. Saaty på 1970-talet; Saaty samarbetade med Ernest Forman för att utveckla Expert Choice 1983, och AHP har studerats och förfinats omfattande sedan dess. Det representerar en korrekt metod för att kvantifiera vikten av beslutskriterier. Individuella experters erfarenheter används för att uppskatta faktorers relativa storlek genom parvisa jämförelser. Var och en av respondenterna jämför den relativa betydelsen av varje par av objekt med hjälp av ett speciellt utformat frågeformulär.

Användningsområden och tillämpningar

AHP har särskild tillämpning i gruppbeslutsfattande och används över hela världen i en mängd olika beslutssituationer , inom områden som regering, näringsliv, industri, hälsovård och utbildning.

Istället för att föreskriva ett "korrekt" beslut, hjälper AHP beslutsfattare att hitta det som bäst passar deras mål och deras förståelse av problemet. Det ger en omfattande och rationell ram för att strukturera ett beslutsproblem, för att representera och kvantifiera dess delar, för att relatera dessa element till övergripande mål och för att utvärdera alternativa lösningar.

Användare av AHP delar först upp sina beslutsproblem i en hierarki av mer lättfattliga delproblem, som vart och ett kan analyseras oberoende. Elementen i hierarkin kan relatera till vilken aspekt som helst av beslutsproblemet – påtaglig eller immateriell, noggrant uppmätt eller grovt uppskattad, väl eller dåligt förstådd – vad som helst som gäller det aktuella beslutet.

När hierarkin väl är uppbyggd utvärderar beslutsfattarna systematiskt dess olika element genom att jämföra dem med varandra två åt gången, med avseende på deras inverkan på ett element ovanför dem i hierarkin. I jämförelserna kan beslutsfattarna använda konkreta data om elementen, men de använder vanligtvis sina bedömningar om elementens relativa betydelse och betydelse. Det är kärnan i AHP att mänskliga bedömningar, och inte bara den underliggande informationen, kan användas för att utföra utvärderingarna.

AHP omvandlar dessa utvärderingar till numeriska värden som kan bearbetas och jämföras över hela problemets omfång. En numerisk vikt eller prioritet härleds för varje element i hierarkin, vilket gör det möjligt att jämföra olika och ofta injämförbara element med varandra på ett rationellt och konsekvent sätt. Denna förmåga skiljer AHP från andra beslutsfattande tekniker.

I det sista steget av processen beräknas numeriska prioriteringar för vart och ett av beslutsalternativen. Dessa siffror representerar alternativens relativa förmåga att uppnå beslutsmålet, så de tillåter en enkel övervägande av de olika handlingssätten.

Flera företag tillhandahåller datorprogramvara för att hjälpa till att använda processen. [ förtydligande behövs ] Även om den kan användas av individer som arbetar med enkla beslut, är den analytiska hierarkiprocessen (AHP) mest användbar där grupper av människor arbetar med komplexa problem, särskilt de med höga insatser, som involverar mänskliga uppfattningar och bedömningar, vars lösningar få långsiktiga återverkningar. Det har unika fördelar när viktiga delar av beslutet är svåra att kvantifiera eller jämföra, eller där kommunikationen mellan teammedlemmar hindras av deras olika specialiseringar, terminologier eller perspektiv.

Beslutssituationer som AHP kan tillämpas på inkluderar:

  • Val – Valet av ett alternativ från en given uppsättning alternativ, vanligtvis när det finns flera beslutskriterier inblandade.
  • Rangordning – Ordna en uppsättning alternativ från mest till minst önskvärt.
  • Prioritering – Att bestämma den relativa förtjänsten för medlemmar i en uppsättning alternativ, i motsats till att välja ett enda eller bara rangordna dem
  • Resursallokering – Fördelning av resurser mellan en uppsättning alternativ
  • Benchmarking – Att jämföra processerna i den egna organisationen med processerna i andra branschorganisationer
  • Kvalitetsledning – Att hantera de flerdimensionella aspekterna av kvalitet och kvalitetsförbättring
  • Konfliktlösning – Att lösa tvister mellan parter med uppenbarligen oförenliga mål eller positioner

AHP:s tillämpningar på komplexa beslutssituationer har uppgått till tusentals och har gett omfattande resultat i problem med planering , resursallokering , prioritering och urval bland alternativ. Andra områden har inkluderat prognoser , total kvalitetsstyrning , omstrukturering av affärsprocesser , implementering av kvalitetsfunktioner och det balanserade styrkortet . Många AHP-applikationer rapporteras aldrig till världen i stort, eftersom de äger rum på höga nivåer av stora organisationer där säkerhets- och integritetshänsyn förbjuder att de avslöjas. Men vissa användningsområden för AHP diskuteras i litteraturen. Nyligen har dessa inkluderat:

AHP används ibland för att utforma mycket specifika procedurer för särskilda situationer, såsom bedömning av byggnader efter historisk betydelse. Det applicerades nyligen på ett projekt som använder videofilmer för att bedöma tillståndet på motorvägarna i Virginia . Motorvägsingenjörer använde det först för att bestämma den optimala omfattningen av projektet och sedan för att motivera budgeten för lagstiftarna .

Vikterna för AHP-bedömningsmatrisen kan korrigeras med de som beräknats genom entropimetoden. Denna variant av AHP-metoden kallas AHP-EM.

Utbildning och vetenskaplig forskning

Även om användningen av den analytiska hierarkiprocessen inte kräver någon specialiserad akademisk utbildning, anses det vara ett viktigt ämne i många institutioner för högre utbildning, inklusive ingenjörsskolor och handelshögskolor . Det är ett särskilt viktigt ämne inom kvalitetsområdet och lärs ut i många specialiserade kurser inklusive Six Sigma , Lean Six Sigma och QFD .

Värdet av AHP är erkänt i utvecklade länder och utvecklingsländer runt om i världen. Kina är ett exempel – nästan hundra kinesiska universitet erbjuder kurser i AHP, och många doktorander väljer AHP som ämne för sin forskning och sina avhandlingar. Över 900 artiklar har publicerats om ämnet i Kina, och det finns åtminstone en kinesisk vetenskaplig tidskrift som uteslutande ägnas åt AHP.

International Symposium on the Analytic Hierarchy Process ( ISAHP) håller vartannat år möten för akademiker och praktiker som är intresserade av området. Ett brett spektrum av ämnen tas upp. De under 2005 sträckte sig från "Etablishing Payment Standards for Surgical Specialists", till "Strategic Technology Roadmapping", till "Infrastructure Reconstruction in Devastated Countries". Vid mötet 2007 i Valparaíso, Chile , presenterades över 90 dokument från 19 länder, inklusive USA, Tyskland, Japan, Chile, Malaysia och Nepal. Ett liknande antal artiklar presenterades vid symposiet 2009 i Pittsburgh, Pennsylvania , då 28 länder var representerade. Ämnena för uppsatserna var ekonomisk stabilisering i Lettland , portföljurval inom banksektorn, Wildfire Management för att mildra den globala uppvärmningen och landsbygdsmikroprojekt i Nepal .

Använda sig av

En typisk enhet för att ange bedömningar i en AHP-gruppbeslutssession

Som kan ses i materialet som följer, innebär användning av AHP en matematisk syntes av många bedömningar om beslutsproblemet. Det är inte ovanligt att dessa domar uppgår till dussintals eller till och med hundratals. Även om matematiken kan göras för hand eller med en miniräknare, är det mycket vanligare att använda en av flera datoriserade metoder för att mata in och syntetisera domarna. Den enklaste av dessa involverar standardkalkylprogram, medan den mest komplexa använder anpassad programvara, ofta utökad med speciella anordningar för att inhämta bedömningar från beslutsfattare samlade i ett mötesrum.

Proceduren för att använda AHP kan sammanfattas som:

  1. Modellera problemet som en hierarki som innehåller beslutsmålet, alternativen för att nå det och kriterierna för att utvärdera alternativen.
  2. Upprätta prioriteringar bland elementen i hierarkin genom att göra en serie bedömningar baserade på parvisa jämförelser av elementen. Till exempel, när man jämför potentiella köp av kommersiella fastigheter, kan investerarna säga att de föredrar läge framför pris och pris framför tidpunkt.
  3. Syntetisera dessa bedömningar för att ge en uppsättning övergripande prioriteringar för hierarkin. Detta skulle kombinera investerarnas bedömningar om läge, pris och tidpunkt för fastigheterna A, B, C och D till övergripande prioriteringar för varje fastighet.
  4. Kontrollera konsekvensen i domarna.
  5. Kom till ett slutgiltigt beslut baserat på resultaten av denna process.

Dessa steg beskrivs mer utförligt nedan.

Modellera problemet som en hierarki

Det första steget i den analytiska hierarkiprocessen är att modellera problemet som en hierarki. Genom att göra detta utforskar deltagarna aspekterna av problemet på nivåer från allmänt till detaljerat, och uttrycker det sedan på det sätt på flera nivåer som AHP kräver. När de arbetar med att bygga hierarkin ökar de sin förståelse för problemet, av dess sammanhang och av varandras tankar och känslor om båda.

Hierarkier definierade

En hierarki är ett stratifierat system för att rangordna och organisera människor, saker, idéer etc., där varje element i systemet, förutom det översta, är underordnat ett eller flera andra element. Även om begreppet hierarki är lätt att förstå intuitivt, kan det också beskrivas matematiskt. Diagram över hierarkier är ofta formade ungefär som pyramider, men förutom att ha ett enda element överst, finns det inget nödvändigtvis pyramidformat med en hierarki.

Mänskliga organisationer är ofta strukturerade som hierarkier, där det hierarkiska systemet används för att tilldela ansvar, utöva ledarskap och underlätta kommunikation. Bekanta hierarkier av "saker" inkluderar en stationär dators tornenhet högst upp, med dess underordnade bildskärm, tangentbord och mus "under".

I idévärlden använder vi hierarkier för att hjälpa oss att skaffa oss detaljerad kunskap om den komplexa verkligheten: vi strukturerar verkligheten i dess beståndsdelar, och dessa i sin tur till sina egna beståndsdelar, och fortsätter nedför hierarkin så många nivåer som vi vill. Vid varje steg fokuserar vi på att förstå en enskild komponent i helheten, tillfälligt bortse från de andra komponenterna på denna och alla andra nivåer. När vi går igenom denna process ökar vi vår globala förståelse av vilken komplex verklighet vi än studerar.

Tänk på den hierarki som läkarstudenter använder sig av när de lär sig anatomi – de överväger separat muskuloskeletala systemet (inklusive delar och underdelar som handen och dess ingående muskler och ben), cirkulationssystemet (och dess många nivåer och grenar), nervsystemet ( och dess många komponenter och delsystem), etc., tills de har täckt alla system och de viktiga underavdelningarna av var och en. Avancerade elever fortsätter indelningen hela vägen till nivån av cellen eller molekylen. I slutändan förstår eleverna den "stora bilden" och ett stort antal av dess detaljer. Inte bara det, utan de förstår de enskilda delarnas relation till helheten. Genom att arbeta hierarkiskt har de fått en omfattande förståelse för anatomi.

På liknande sätt, när vi närmar oss ett komplext beslutsproblem, kan vi använda en hierarki för att integrera stora mängder information i vår förståelse av situationen. När vi bygger upp denna informationsstruktur bildar vi oss en bättre och bättre bild av problemet som helhet.

Hierarkier i AHP

En AHP-hierarki är ett strukturerat sätt att modellera beslutet. Den består av ett övergripande mål, en grupp alternativ eller alternativ för att nå målet och en grupp faktorer eller kriterier som relaterar alternativen till målet. Kriterierna kan delas upp ytterligare i delkriterier, delkriterier och så vidare, på så många nivåer som problemet kräver. Ett kriterium kanske inte gäller enhetligt, men kan ha graderade skillnader som att lite sötma är njutbart men för mycket sötma kan vara skadligt. I så fall delas kriteriet in i underkriterier som indikerar olika intensiteter av kriteriet, som: liten, medelhög, hög och dessa intensiteter prioriteras genom jämförelser under moderkriteriet, sötma. Publicerade beskrivningar av AHP-applikationer inkluderar ofta diagram och beskrivningar av deras hierarkier; några enkla visas i den här artikeln. Mer komplexa AHP-hierarkier har samlats och tryckts om i minst en bok. Mer komplexa hierarkier finns på en speciell diskussionssida för den här artikeln .

Utformningen av varje AHP-hierarki kommer att bero inte bara på problemets natur, utan också på kunskap, bedömningar, värderingar, åsikter, behov, önskemål etc. hos deltagarna i beslutsprocessen. Att konstruera en hierarki innebär vanligtvis betydande diskussioner, forskning och upptäckter av de inblandade. Även efter den ursprungliga konstruktionen kan den ändras för att tillgodose nyligen genomtänkta kriterier eller kriterier som inte ursprungligen ansågs vara viktiga; alternativ kan också läggas till, raderas eller ändras.

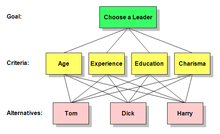
För att bättre förstå AHP-hierarkier, överväg ett beslutsproblem med ett mål som ska nås, tre alternativa sätt att nå målet och fyra kriterier mot vilka alternativen måste mätas.

En sådan hierarki kan visualiseras som ett diagram som det omedelbart nedan, med målet överst, de tre alternativen längst ner och de fyra kriterierna däremellan. Det finns användbara termer för att beskriva delarna av sådana diagram: Varje ruta kallas en nod. En nod som är ansluten till en eller flera noder på en nivå under den kallas en föräldernod. Noderna som den är så ansluten till kallas dess barn.

Genom att tillämpa dessa definitioner på diagrammet nedan, är målet föräldern till de fyra kriterierna, och de fyra kriterierna är underordnade av målet. Varje kriterium är en förälder till de tre alternativen. Observera att det bara finns tre alternativ, men i diagrammet upprepas var och en av dem under var och en av sina föräldrar.

En enkel AHP-hierarki. Det finns tre alternativ för att nå målet och fyra kriterier som ska användas för att avgöra bland dem.

För att minska storleken på ritningen som krävs är det vanligt att representera AHP-hierarkier som visas i diagrammet nedan, med endast en nod för varje alternativ, och med flera linjer som förbinder alternativen och de kriterier som gäller för dem. För att undvika skräp, utelämnas dessa rader ibland eller minskas i antal. Oavsett sådana förenklingar i diagrammet är varje kriterium individuellt kopplat till alternativen i den faktiska hierarkin. Linjerna kan tänkas vara riktade nedåt från föräldern i en nivå till dess barn på nivån under.

AHP-hierarki för att välja en ledare. Det finns ett mål, tre kandidater och fyra kriterier för att välja bland dem.

Utvärdera hierarkin

När hierarkin väl har konstruerats analyserar deltagarna den genom en serie parvisa jämförelser som härleder numeriska mätskalor för noderna. Kriterierna jämförs parvis mot målet för betydelse. Alternativen jämförs parvis mot vart och ett av kriterierna för preferens. Jämförelserna bearbetas matematiskt och prioriteringar härleds för varje nod.

Betrakta exemplet "Välj en ledare" ovan. En viktig uppgift för beslutsfattarna är att bestämma vilken vikt som ska ges varje kriterium vid valet av ledare. En annan viktig uppgift är att fastställa vilken vikt som ska ges till varje kandidat med hänsyn till vart och ett av kriterierna. AHP låter dem inte bara göra det, utan den låter dem sätta ett meningsfullt och objektivt numeriskt värde på vart och ett av de fyra kriterierna.

Till skillnad från de flesta undersökningar som använder femgradig Likert-skalan , är AHP:s frågeformulär 9 till 1 till 9.

Fastställ prioriteringar

Det här avsnittet förklarar prioriteringar, visar hur de upprättas och ger ett enkelt exempel.

Prioriteringar definierade och förklarade

Prioriteter är nummer associerade med noderna i en AHP-hierarki. De representerar den relativa vikten av noderna i vilken grupp som helst.

Precis som sannolikheter är prioriteter absoluta tal mellan noll och ett, utan enheter eller dimensioner. En nod med prioritet .200 har dubbelt så stor vikt för att nå målet som en med prioritet .100, tio gånger vikten av en med prioritet .020 och så vidare. Beroende på det aktuella problemet kan "vikt" hänvisa till vikt, preferens, eller sannolikhet, eller vilken faktor som än tas i beaktande av beslutsfattarna.

Prioriteter fördelas över en hierarki enligt dess arkitektur, och deras värden beror på den information som matas in av användarna av processen. Prioriteringarna för målet, kriterierna och alternativen är intimt relaterade, men måste övervägas separat.

Per definition är målets prioritet 1 000. Prioriteringarna för alternativen summerar alltid till 1 000. Saker och ting kan bli komplicerade med flera nivåer av kriterier, men om det bara finns en nivå ökar deras prioriteringar också till 1 000. Allt detta illustreras av prioriteringarna i exemplet nedan.

Enkel AHP-hierarki med tillhörande standardprioriteringar

Observera att prioriteringarna på varje nivå i exemplet – målet, kriterierna och alternativen – alla summerar till 1 000.

Prioriteringarna som visas är de som finns innan någon information har matats in om vikter av kriterierna eller alternativen, så prioriteringarna inom varje nivå är alla lika. De kallas hierarkins standardprioriteringar. Om ett femte kriterium lades till i denna hierarki, skulle standardprioriteten för varje kriterium vara .200. Om det bara fanns två alternativ skulle var och en ha en standardprioritet på .500.

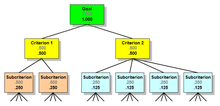
Två ytterligare begrepp gäller när en hierarki har mer än en nivå av kriterier: lokala prioriteringar och globala prioriteringar. Betrakta hierarkin som visas nedan, som har flera underkriterier under varje kriterium.

En mer komplex AHP-hierarki, med lokala och globala standardprioriteringar. För tydlighetens skull framgår inte beslutsalternativen i diagrammet.

De lokala prioriteringarna, som visas i grått, representerar den relativa vikten av noderna inom en syskongrupp i förhållande till deras förälder. De lokala prioriteringarna för varje grupp av kriterier och deras syskonunderkriterier uppgår till 1 000. De globala prioriteringarna, som visas i svart, erhålls genom att multiplicera syskonens lokala prioriteringar med deras förälders globala prioritet. De globala prioriteringarna för alla underkriterier i nivån uppgår till 1 000.

Regeln är denna: Inom en hierarki summeras de globala prioriteringarna för underordnade noder alltid till den globala prioriteten för deras förälder. Inom en grupp barn uppgår de lokala prioriteringarna till 1 000.

Hittills har vi bara tittat på standardprioriteringar. När den analytiska hierarkiprocessen går framåt kommer prioriteringarna att ändras från sina standardvärden när beslutsfattarna matar in information om de olika nodernas betydelse. De gör detta genom att göra en serie parvisa jämförelser.

Praktiska exempel

Erfarna utövare vet att det bästa sättet att förstå AHP är att arbeta igenom fall och exempel. Två detaljerade fallstudier , specifikt utformade som djupgående undervisningsexempel, tillhandahålls som bilagor till den här artikeln:

Några av böckerna om AHP innehåller praktiska exempel på dess användning, även om de vanligtvis inte är avsedda att vara steg-för-steg-inlärningshjälpmedel. Ett av dem innehåller en handfull utökade exempel, plus cirka 400 AHP-hierarkier kortfattat beskrivna och illustrerade med figurer. Många exempel diskuteras, mestadels för professionell publik, i artiklar publicerade av International Symposium on the Analytic Hierarchy Process .

Kritik

AHP ingår i de flesta läroböcker för operationsforskning och managementvetenskap , och lärs ut vid ett flertal universitet; den används flitigt i organisationer som noggrant har undersökt dess teoretiska grund. Även om den allmänna konsensusen är att den är både tekniskt giltig och praktiskt användbar, har metoden sina kritiker. I början av 1990-talet publicerades en serie debatter mellan kritiker och förespråkare av AHP i Management Science och The Journal of the Operational Research Society, två prestigefyllda tidskrifter där Saaty och hans kollegor hade stort inflytande. Dessa debatter verkar ha avgjorts till förmån för AHP:

  • En djupgående artikel som diskuterar och motbevisar den akademiska kritiken av AHP publicerades i Operations Research 2001.
  • Ett 2008 års Management Science- dokument som granskade 15 års framsteg inom alla områden av multikriteriumbeslutsfattande visade att AHP-publikationer vida har överträffat dem inom något annat område, vilket karakteriserar deras tillväxt som "enorm".
  • Även 2008 erkände det stora sällskapet för operationsforskning, Institutet för operationsforskning och managementvetenskaperna formellt AHP:s breda inverkan på sina områden.

Enstaka kritik förekommer fortfarande. En artikel från 1997 undersökte möjliga brister i den verbala (vs. numeriska) skalan som ofta används i AHP parvisa jämförelser. En annan från samma år hävdade att ofarliga förändringar av AHP-modellen kan införa ordning där ingen ordning existerar. Ett dokument från 2006 fann att tillägget av kriterier för vilka alla alternativ presterar lika kan förändra alternativens prioriteringar.

År 2021 publicerades den första omfattande utvärderingen av AHP i en bok författad av två akademiker från Valencias tekniska universitet och Universidad Politécnica de Cartagena, och publicerad av Springer Nature . Baserat på en empirisk undersökning och objektiva vittnesmål från 101 forskare fann studien minst 30 brister i AHP och fann den olämplig för komplexa problem, och i vissa situationer även för små problem.

Rangvändning

Beslutsfattande innebär att alternativ rangordnas i termer av kriterier eller attribut för dessa alternativ. Det är ett axiom för vissa beslutsteorier att när nya alternativ läggs till ett beslutsproblem, får rangordningen av de gamla alternativen inte förändras - att " rangomkastning " inte får ske.

Det finns två tankar om rangvändning. Man hävdar att nya alternativ som inte introducerar några ytterligare attribut inte bör orsaka rangförändring under några omständigheter. Den andra hävdar att det finns vissa situationer där rangändring rimligen kan förväntas. Den ursprungliga formuleringen av AHP tillät rangvändningar. 1993 introducerade Forman ett andra AHP-syntesläge, kallat det ideala syntesläget, för att hantera valsituationer där tillägg eller borttagning av ett "irrelevant" alternativ inte borde och inte kommer att orsaka en förändring i rangordningen av befintliga alternativ. Den nuvarande versionen av AHP kan rymma båda dessa skolor - dess idealläge bevarar rang, medan dess distributionsläge tillåter rangordningar att ändras. Båda lägena väljs beroende på problemet.

Rank reversal och AHP diskuteras utförligt i en artikel från 2001 i Operations Research , samt ett kapitel med titeln Rank Preservation and Reversal, i den aktuella grundboken om AHP. Den senare presenterar publicerade exempel på rangomvändning på grund av att man lägger till kopior och nästan kopior av ett alternativ, på grund av intransitivitet av beslutsregler, på grund av att man lägger till fantom- och lockbetsalternativ och på grund av omkopplingsfenomenet i hjälpfunktioner. Den diskuterar också AHP:s fördelnings- och idealläge.

En ny form av rangomvändning av AHP hittades 2014 där AHP producerar rangordningsomkastning vid eliminering av irrelevant data, detta är data som inte särskiljer alternativ.

Det finns olika typer av rangförändringar. Även andra metoder förutom AHP kan uppvisa sådana rangomvändningar. Mer diskussion om rangvändningar med AHP och andra MCDM-metoder finns på sidan för rangomvändningar i beslutsfattande .

Icke-monotonicitet hos vissa viktextraktionsmetoder

Inom en jämförelsematris kan man ersätta en bedömning med en mindre gynnsam bedömning och sedan kontrollera om indikationen av den nya prioriteringen blir mindre gynnsam än den ursprungliga prioriteringen. I samband med turneringsmatriser har det bevisats av Oskar Perron att den huvudsakliga högra egenvektormetoden inte är monoton. Detta beteende kan också påvisas för reciproka nxn-matriser, där n > 3. Alternativa tillvägagångssätt diskuteras på annat håll.

Se även

Vidare läsning

  •     Saaty, Thomas L. Beslutsfattande för ledare: Den analytiska hierarkiprocessen för beslut i en komplex värld ( 1982). Belmont, Kalifornien: Wadsworth. ISBN 0-534-97959-9 ; Pocketbok, Pittsburgh: RWS. ISBN 0-9620317-0-4 . "Fokuserar på praktisk tillämpning av AHP; täcker kort teori."
  •   Saaty, Thomas L. Fundamentals of Decision Making and Priority Theory with the Analytic Hierarchy Process ( 1994). Pittsburgh: RWS. ISBN 0-9620317-6-3 . "En grundlig beskrivning av de teoretiska aspekterna av AHP."
  •   Saaty, Thomas L. Matematiska principer för beslutsfattande (Principia Mathematica Decernendi) ( 2009). Pittsburgh: RWS. ISBN 1-888603-10-0 . "Omfattande bevakning av AHP, dess efterträdare ANP och vidareutveckling av deras underliggande koncept."
  •   Saaty, Thomas L., med Ernest H. Forman. The Hierarchon: A Dictionary of Hierarchies . (1992) Pittsburgh: RWS. ISBN 0-9620317-5-5 . "Dusintals illustrationer och exempel på AHP-hierarkier. En början klassificering av idéer som rör planering, konfliktlösning och beslutsfattande."
  •       Saaty, Thomas L., med Luis G. Vargas Prioriteternas logik: tillämpningar inom näringsliv, energi, hälsa och transport ( 1982). Boston: Kluwer-Nijhoff. ISBN 0-89838-071-5 (Inbunden) ISBN 0-89838-078-2 (Paperback). Återpublicerad 1991 av RWS, ISBN 1-888603-07-0 .
  • Kardi Teknomo. Handledning för analytisk hierarkiprocess (2012). Revoledu.
  •     Kearns, Kevin P.; Saaty, Thomas L. Analytisk planering: Systemens organisation (1985). Oxford: Pergamon Press. ISBN 0-08-032599-8 . Återpublicerad 1991 av RWS, ISBN 1-888603-07-0 .
  •   med Joyce Alexander. Konfliktlösning: Den analytiska hierarkiprocessen (1989). New York: Praeger. ISBN 0-275-93229-X
  •   Vargas, Luis L.; Saaty, Thomas L. Prediction, Projection and Forecasting: Applications of the Analytic Hierarchy Process in Economics, Finance, Politics, Games and Sports ( 1991). Boston: Kluwer Academic. ISBN 0-7923-9104-7
  •   Vargas, Luis L.; Saaty, Thomas L. Beslutsfattande i ekonomiska, sociala och tekniska miljöer ( 1994). Pittsburgh: RWS. ISBN 0-9620317-7-1
  •   Vargas, Luis L.; Saaty, Thomas L. Modeller, metoder, koncept och tillämpningar av den analytiska hierarkiprocessen ( 2001). Boston: Kluwer Academic. ISBN 0-7923-7267-0
  •   Peniwati, Kirti; Vargas, Luis L. Gruppbeslutsfattande: Drawing Out and Reconciliing Differences (2007). Pittsburgh: RWS. ISBN 1-888603-08-9

externa länkar

Hämtad från " https://en.wikipedia.org/w/index.php?title=Analytic_hierarchy_process&oldid=1131805792 "