Vågledare filter

Figur 1 . Vågledarepostfilter: ett bandpassfilter som består av en längd på WG15 (en standardvågledarstorlek för X-bandsanvändning ) uppdelat i en rad med fem kopplade resonanshålrum med stängsel med tre stolpar vardera. Ändarna av stolparna kan ses sticka ut genom guidens vägg.

Ett vågledarfilter är ett elektroniskt filter konstruerat med vågledarteknik . Vågledare är ihåliga metallkanaler inuti vilka en elektromagnetisk våg kan sändas. Filter är enheter som används för att låta signaler på vissa frekvenser passera (passbandet ), medan andra avvisas ( stoppbandet ) . Filter är en grundläggande komponent i elektronikkonstruktioner och har många tillämpningar. Dessa inkluderar val av signaler och begränsning av brus . Vågledarfilter är mest användbara i mikrovågsbandet av frekvenser, där de har en lämplig storlek och har låg förlust . Exempel på mikrovågsfilter finns i satellitkommunikation , telefonnät och TV-sändningar .

Vågledarfilter utvecklades under andra världskriget för att möta behoven av radar och elektroniska motåtgärder , men hittade efteråt snart civila tillämpningar som användning i mikrovågslänkar . Mycket av utvecklingen efter kriget handlade om att minska volymen och vikten av dessa filter, först genom att använda nya analystekniker som ledde till eliminering av onödiga komponenter, sedan av innovationer som hålrum i två lägen och nya material som keramiska resonatorer .

En speciell egenskap hos vågledarfilterdesignen gäller transmissionssättet . System baserade på par av ledande ledningar och liknande teknologier har bara ett överföringssätt. I vågledarsystem är valfritt antal moder möjliga. Detta kan vara både en nackdel, eftersom falska moder ofta orsakar problem, och en fördel, eftersom en dubbelmodsdesign kan vara mycket mindre än den ekvivalenta vågledarens enkelmodsdesign. De främsta fördelarna med vågledarfilter jämfört med andra teknologier är deras förmåga att hantera hög effekt och deras låga förlust. De främsta nackdelarna är deras volym och kostnad jämfört med teknologier som mikrostripfilter .

Det finns ett brett utbud av olika typer av vågledarfilter. Många av dem består av en kedja av kopplade resonatorer av något slag som kan modelleras som ett stegnätverk av LC-kretsar . En av de vanligaste typerna består av ett antal kopplade resonanshålrum . Även inom denna typ finns det många undertyper, mestadels differentierade med hjälp av koppling . Dessa kopplingstyper inkluderar öppningar, ^[w] iris, ^[x] och stolpar. Andra vågledarfiltertyper inkluderar dielektriska resonatorfilter , insatsfilter, finlinefilter, korrugerade vågledarfilter och stubbfilter. Ett antal vågledarkomponenter har filterteori tillämpad på sin design, men deras syfte är något annat än att filtrera signaler. Sådana enheter inkluderar impedansmatchande komponenter, riktningskopplare och diplexrar . Dessa enheter tar ofta formen av ett filter, åtminstone delvis.

Omfattning

Den vanliga innebörden av vågledare , när termen används okvalificerad, är den ihåliga metalltypen (eller ibland dielektrisk fylld), men andra vågledartekniker är möjliga. Omfattningen av denna artikel är begränsad till typen av metallrör. Vågledarstrukturen efter väggen är något av en variant, men är besläktad nog att inkludera i den här artikeln - vågen är mestadels omgiven av ledande material. Det är möjligt att konstruera vågledare av dielektriska stavar , det mest välkända exemplet är optiska fibrer . Detta ämne ligger utanför artikelns omfång med undantaget att dielektriska stavresonatorer ibland används inuti ihåliga metallvågledare. Transmission line ^[o] teknologier som ledande ledningar och mikrostrip kan ses som vågledare, men kallas inte vanligtvis sådana och ligger också utanför denna artikels omfattning.

Grundläggande koncept

Filter

Inom elektronik används filter för att låta signaler från ett visst frekvensband passera samtidigt som andra blockeras . De är en grundläggande byggsten i elektroniska system och har många tillämpningar. Bland användningarna av vågledarfilter är konstruktionen av duplexer , diplexer , ^[d] och multiplexorer ; selektivitet och brusbegränsning i mottagare ; och av harmonisk distorsion i sändare .

Vågledare

Vågledare är metallkanaler som används för att begränsa och rikta radiosignaler. De är oftast gjorda av mässing, men även aluminium och koppar används. Vanligtvis är de rektangulära, men andra tvärsnitt som cirkulära eller elliptiska är möjliga. Ett vågledarfilter är ett filter som består av vågledarkomponenter. Den har ungefär samma användningsområde som andra filterteknologier inom elektronik och radioteknik men är väldigt annorlunda mekaniskt och i princip i drift.

Tekniken som används för att konstruera filter väljs till stor del av den förväntade driftfrekvensen, även om det finns en stor överlappning. Lågfrekvensapplikationer som ljudelektronik använder filter som består av diskreta kondensatorer och induktorer . Någonstans i det mycket höga frekvensbandet går designers över till att använda komponenter gjorda av delar av transmissionsledningar. ^[p] Den här typen av design kallas distribuerade elementfilter . Filter gjorda av diskreta komponenter kallas ibland klumpade element för att särskilja dem. Vid ännu högre frekvenser, mikrovågsbanden , växlar designen till vågledarfilter, eller ibland en kombination av vågledare och transmissionsledningar.

Vågledarfilter har mycket mer gemensamt med transmissionsledningsfilter än filter med klumpade element; de innehåller inga diskreta kondensatorer eller induktorer. Emellertid kan vågledardesignen ofta vara likvärdig (eller ungefär så) med en klumpad elementdesign. Utformningen av vågledarfilter utgår faktiskt ofta från en klumpad elementdesign och omvandlar sedan elementen i den designen till vågledarkomponenter.

Lägen

Figur 2. Fältmönstren för några vanliga vågledarmoder

En av de viktigaste skillnaderna i driften av vågledarfilter jämfört med transmissionsledningskonstruktioner gäller överföringssättet för den elektromagnetiska vågen som bär signalen. I en transmissionsledning är vågen associerad med elektriska strömmar på ett par ledare. Ledarna begränsar strömmarna till att vara parallella med linjen, och följaktligen är både de magnetiska och elektriska komponenterna i det elektromagnetiska fältet vinkelräta mot vågens färdriktning. Detta tvärgående läge betecknas TEM ^[l] (tvärgående elektromagnetisk). Å andra sidan finns det oändligt många lägen som vilken helt ihålig vågledare som helst kan stödja, men TEM-läget är inte ett av dem. Vågledarmoder betecknas antingen TE ^[m] (transversell elektrisk) eller TM ^[n] (transversell magnetisk), följt av ett par suffix som identifierar den exakta moden.

Denna mångfald av moder kan orsaka problem i vågledarfilter när falska moder genereras. Design är vanligtvis baserad på ett enda läge och innehåller ofta funktioner för att undertrycka de oönskade lägena. Å andra sidan kan man ha fördelar av att välja rätt läge för applikationen och till och med ibland använda mer än ett läge samtidigt. Där endast ett enda läge används kan vågledaren modelleras som en ledande transmissionsledning och resultat från transmissionsledningsteori kan tillämpas.

Cutoff

₀ En annan egenskap som är speciell för vågledarfilter är att det finns en bestämd frekvens, gränsfrekvensen , under vilken ingen överföring kan ske. Detta innebär att lågpassfilter i teorin inte kan tillverkas i vågledare. Emellertid tar konstruktörer ofta en lågpassfilterdesign med klumpade element och konverterar den till en vågledarimplementering. Filtret är följaktligen lågpassigt designat och kan betraktas som ett lågpassfilter för alla praktiska ändamål om gränsfrekvensen är under någon frekvens av intresse för applikationen. Vågledarens gränsfrekvens är en funktion av överföringsmoden, så vid en given frekvens kan vågledaren vara användbar i vissa moder men inte andra. På samma sätt beror styrvåglängden ^[h] (λg ₎ och den karakteristiska impedansen ^[b] ( Z ) för guiden vid en given frekvens också på moden.

Dominant läge

Läget med den lägsta gränsfrekvensen av alla lägen kallas det dominanta läget. Mellan cutoff och näst högsta läge är detta det enda läget det är möjligt att sända, varför det beskrivs som dominant. Eventuella falska moder som genereras dämpas snabbt längs styrningens längd och försvinner snart. Praktiska filterkonstruktioner görs ofta för att fungera i det dominerande läget.

I rektangulär vågledare är TE ₁₀ ^[q] -moden (visad i figur 2) den dominerande moden. Det finns ett band av frekvenser mellan den dominanta modgränsen och den näst högsta modskärningen i vilken vågledaren kan drivas utan någon möjlighet att generera falska moder. De näst högsta cutoff-lägena är TE20 _, [ ^r] vid exakt två gånger TE _10- moden och TE ₀₁ ^[s] som också är två gånger TE ₁₀ om den använda vågledaren har det vanligen använda bildförhållandet 2:1. Det lägsta cutoff TM-läget är TM ₁₁ ^[t] (visas i figur 2) vilket är $\scriptstyle {\sqrt {5}}$ gånger det dominanta läget i 2:1-vågledaren. Således finns det en oktav över vilken den dominerande moden är fri från falska moder, även om drift för nära cutoff vanligtvis undviks på grund av fasdistorsion.

I cirkulär vågledare är den dominerande moden TE ₁₁ ^[u] och visas i figur 2. Den näst högsta moden är TM ₀₁ . ^[v] Området över vilket den dominanta moden garanteras vara fri från falskt läge är mindre än i rektangulär vågledare; förhållandet mellan högsta och lägsta frekvens är ungefär 1,3 i cirkulär vågledare, jämfört med 2,0 i rektangulär ledare.

Evanescent lägen

Huvudartikel: Evanescent wave

Evanescent-lägen är lägen under gränsfrekvensen. De kan inte fortplanta sig nerför vågledaren på något avstånd och dö bort exponentiellt. De är emellertid viktiga för funktionen hos vissa filterkomponenter såsom iris och stolpar, som beskrivs senare, eftersom energi lagras i de evanescenta vågfälten.

Fördelar och nackdelar

Liksom transmissionsledningsfilter har vågledarfilter alltid flera passband , kopior av prototypen med klumpade element . I de flesta konstruktioner är endast det lägsta frekvenspassbandet användbart (eller lägsta två i fallet med bandstoppfilter ) och resten anses vara oönskade falska artefakter. Detta är en inneboende egenskap hos tekniken och kan inte utformas, även om design kan ha viss kontroll över frekvenspositionen för de falska banden. Följaktligen, i varje given filterkonstruktion, finns det en övre frekvens bortom vilken filtret kommer att misslyckas med att utföra sin funktion. Av denna anledning kan äkta lågpass- och högpassfilter inte existera i vågledaren. Vid någon hög frekvens kommer det att finnas ett falskt passband eller stoppband som avbryter filtrets avsedda funktion. Men, i likhet med situationen med vågledarens gränsfrekvens, kan filtret utformas så att kanten på det första falska bandet ligger långt över alla intressanta frekvenser.

Frekvensintervallet över vilka vågledarfilter är användbara bestäms till stor del av den vågledarstorlek som behövs. Vid lägre frekvenser behöver vågledaren vara opraktisk stor för att hålla gränsfrekvensen under driftfrekvensen. Å andra sidan kan filter vars arbetsfrekvenser är så höga att våglängderna är submillimeter inte tillverkas med normala maskinverkstadsprocesser . Vid så höga frekvenser börjar fiberoptisk teknik bli ett alternativ.

Vågledare är ett medium med låg förlust. Förluster i vågledare kommer oftast från ohmsk förlust orsakad av strömmar inducerade i vågledarväggarna. Rektangulär vågledare har lägre förlust än cirkulär vågledare och är vanligtvis det föredragna formatet, men det cirkulära läget TE ₀₁ har mycket låg förlust och har tillämpningar i långdistanskommunikation. Förlusterna kan minskas genom att polera de inre ytorna på vågledarväggarna. I vissa applikationer som kräver rigorös filtrering är väggarna pläterade med ett tunt lager av guld eller silver för att förbättra ytkonduktiviteten . Ett exempel på sådana krav är satellittillämpningar som kräver låga förluster, hög selektivitet och linjär gruppfördröjning från sina filter.

En av de främsta fördelarna med vågledarfilter jämfört med TEM-lägesteknologier är kvaliteten på deras resonatorer . Resonatorkvalitet kännetecknas av en parameter som kallas Q-faktor , eller bara Q. Q för vågledarresonatorer är i tusental, storleksordningar högre än TEM-modresonatorer. Ledarnas resistans, speciellt i lindade induktorer, begränsar Q för TEM-resonatorer . Detta förbättrade Q leder till bättre presterande filter i vågledare, med större stoppbandsavvisning. Begränsningen till Q i vågledare kommer mestadels från de ohmska förlusterna i väggarna som beskrivits tidigare, men silverplätering av de inre väggarna kan mer än fördubbla Q .

Vågledare har bra effekthanteringsförmåga, vilket leder till filterapplikationer i radar . Trots prestandafördelarna med vågledarfilter mikrostrip ofta den föredragna tekniken på grund av dess låga kostnad. Detta gäller särskilt för konsumentvaror och de lägre mikrovågsfrekvenserna. Microstrip-kretsar kan tillverkas med billig tryckta kretsteknik , och när de integreras på samma tryckta kort som andra kretsblock medför de små extrakostnader.

Historia

Lord Rayleigh föreslog först vågledaröverföring.

Idén med en vågledare för elektromagnetiska vågor föreslogs först av Lord Rayleigh 1897. Rayleigh föreslog att en koaxial transmissionsledning skulle kunna få mittledaren borttagen, och vågor skulle fortfarande fortplanta sig nedåt insidan av den återstående cylindriska ledaren trots att det inte längre fanns en komplett elektrisk krets av ledare. Han beskrev detta i termer av att vågen upprepade gånger reflekterades från den yttre ledarens innervägg i sicksack när den fortskrider nedför vågledaren. Rayleigh var också den första att inse att det fanns en kritisk våglängd, cutoff-våglängden, proportionell mot cylinderdiametern, över vilken vågutbredning inte är möjlig. Intresset för vågledare avtog dock eftersom lägre frekvenser var mer lämpade för långdistansradiokommunikation. Rayleighs resultat glömdes bort för en tid och måste återupptäckas av andra på 1930-talet när intresset för mikrovågor återupplivades. Vågledare utvecklades först, i en cirkulär form, av George Clark Southworth och JF Hargreaves 1932.

Den första analoga filterdesignen som gick utöver en enkel enkel resonator skapades av George Ashley Campbell 1910 och markerade början på filterteorin. Campbells filter var en konstruktion av klumpade element av kondensatorer och induktorer som föreslagits av hans arbete med laddningsspolar . Otto Zobel och andra utvecklade snabbt detta ytterligare. Utvecklingen av distribuerade elementfilter började åren före andra världskriget. En stor uppsats i ämnet publicerades av Mason och Sykes 1937; ett patent inlämnat av Mason 1927 kan innehålla den första publicerade filterdesignen med distribuerade element.

Hans Bethe utvecklade vågledarbländaröppningsteori.

Mason och Sykes arbete var fokuserat på formaten av koaxialkabel och balanserade par av ledningar, men andra forskare tillämpade senare principerna på vågledare också. Mycket utveckling av vågledarfilter genomfördes under andra världskriget drevet av filtreringsbehoven hos radar och elektroniska motåtgärder . En hel del av detta var vid MIT Radiation Laboratory (Rad Lab), men även andra laboratorier i USA och Storbritannien var involverade, såsom Telecommunications Research Establishment i Storbritannien. Bland de välkända forskarna och ingenjörerna vid Rad Lab var Julian Schwinger , Nathan Marcuvitz , Edward Mills Purcell och Hans Bethe . Bethe var bara på Rad Lab en kort tid men producerade sin bländaröppningsteori där. Bländarteori är viktig för vågledarkavitetsfilter, som först utvecklades på Rad Lab. Deras arbete publicerades efter kriget 1948 och inkluderar en tidig beskrivning av dubbellägeshåligheter av Fano och Lawson.

Teoretiskt arbete efter kriget inkluderade den proportionella linjeteorin av Paul Richards . Kommensurerade linjer är nätverk där alla element har samma längd (eller i vissa fall multiplar av enhetslängden), även om de kan skilja sig åt i andra dimensioner för att ge olika karakteristiska impedanser. ^[a] Richards transformation gör att alla klumpade elementdesign kan tas "som de är" och transformeras direkt till en distribuerad elementdesign med hjälp av en mycket enkel transformekvation. 1955 publicerade K. Kuroda omvandlingarna som kallas Kurodas identiteter . Dessa gjorde Richards verk mer användbart i obalanserade och vågledarformat genom att eliminera de problematiska seriekopplade elementen, men det dröjde innan Kurodas japanska verk blev allmänt känt i den engelsktalande världen. En annan teoretisk utveckling var Wilhelm Cauers nätverkssyntesfilter, där han använde Chebyshev-approximationen för att bestämma elementvärden. Cauers arbete utvecklades till stor del under andra världskriget (Cauer dödades mot slutet av det), men kunde inte publiceras allmänt förrän fientligheterna upphörde. Medan Cauers arbete handlar om klumpade element, är det av viss betydelse att vågledarfilter; Chebyshev -filtret , ett specialfall av Cauers syntes, används ofta som ett prototypfilter för vågledardesigner.

Designen på 1950-talet började med en prototyp av klumpat element (en teknik som fortfarande används idag), som efter olika transformationer anlände till det önskade filtret i en vågledarform. Vid den tiden gav detta tillvägagångssätt bråkdelar 1/5 . av bandbredder som inte var mer än cirka 1957 publicerade Leo Young vid Stanford Research Institute en metod för att designa filter som började med en distribuerad elementprototyp, den stegvisa impedansprototypen. Detta filter 2/3 . var baserat på kvartsvågsimpedanstransformatorer av olika bredder och kunde producera design med bandbredder upp till en oktav (en bråkdel av bandbredden på ) Youngs papper tar specifikt upp direktkopplade kavitetsresonatorer, men proceduren kan även tillämpas på andra direktkopplade resonatortyper.

Figur 3. Pierces vågledarimplementering av ett korskopplat filter

Den första publicerade redogörelsen för ett korskopplat filter beror på John R. Pierce vid Bell Labs i ett patent från 1948. Ett korskopplat filter är ett där resonatorer som inte är omedelbart intill är kopplade. De ytterligare frihetsgraderna som sålunda tillhandahålls tillåter designern att skapa filter med förbättrad prestanda, eller alternativt med färre resonatorer. En version av Pierces filter, som visas i figur 3, använder cirkulära vågledarkavitetsresonatorer för att länka mellan rektangulära guidekavitetsresonatorer. Denna princip användes först inte mycket av vågledarfilterdesigners, men den användes flitigt av mekaniska filterdesigners på 1960-talet, särskilt RA Johnson på Collins Radio Company .

Den initiala icke-militära tillämpningen av vågledarfilter var i mikrovågslänkarna som användes av telekommunikationsföretag för att tillhandahålla ryggraden i deras nätverk. Dessa länkar användes även av andra branscher med stora fasta nät, särskilt TV-bolag. Sådana ansökningar var en del av stora kapitalinvesteringsprogram. De används nu även i satellitkommunikationssystem .

Behovet av frekvensoberoende fördröjning i satellittillämpningar ledde till mer forskning om vågledarinkarnationen av korskopplade filter. Tidigare använde satellitkommunikationssystem en separat komponent för fördröjningsutjämning . De ytterligare frihetsgraderna som erhålls från korskopplade filter höll ut möjligheten att designa en platt fördröjning i ett filter utan att kompromissa med andra prestandaparametrar. En komponent som samtidigt fungerade som både filter och equalizer skulle spara värdefull vikt och utrymme. Behoven av satellitkommunikation drev också forskning om de mer exotiska resonatorlägena på 1970-talet. Särskilt framträdande i detta avseende är arbetet av EL Griffin och FA Young, som undersökte bättre lägen för 12-14 GHz- bandet när detta började användas för satelliter i mitten av 1970-talet.

En annan utrymmesbesparande innovation var den dielektriska resonatorn , som kan användas i andra filterformat såväl som vågledare. Den första användningen av dessa i ett filter var av SB Cohn 1965, med titandioxid som dielektriskt material. Dielektriska resonatorer som användes på 1960-talet hade dock mycket dåliga temperaturkoefficienter, vanligtvis 500 gånger sämre än en mekanisk resonator gjord av invar , vilket ledde till instabilitet hos filterparametrarna. Dåtidens dielektriska material med bättre temperaturkoefficienter hade en för låg dielektricitetskonstant för att vara användbara för att spara utrymme. Detta förändrades med introduktionen av keramiska resonatorer med mycket låga temperaturkoefficienter på 1970-talet. Den första av dessa var från Massé och Pucel som använde bariumtetratitanate vid Raytheon 1972. Ytterligare förbättringar rapporterades 1979 av Bell Labs och Murata Manufacturing . Bell Labs barium nonatitanate resonator hade en dielektricitetskonstant på 40 och Q på 5000–10 000 vid 2–7 GHz . Moderna temperaturstabila material har en dielektricitetskonstant på cirka 90 vid mikrovågsfrekvenser, men forskning fortsätter för att hitta material med både låg förlust och hög permittivitet; material med lägre permittivitet, såsom zirkoniumstannat-titanat (ZST) med en dielektricitetskonstant på 38, används fortfarande ibland för sina lågförlustegenskaper.

Ett alternativt tillvägagångssätt för att designa mindre vågledarfilter tillhandahölls genom användningen av icke-utbredning evanescenta lägen. Jaynes och Edson föreslog vågledarfilter i evanescent mode i slutet av 1950-talet. Metoder för att designa dessa filter skapades av Craven och Young 1966. Sedan dess har evanescent mode-vågledarfilter använts framgångsrikt där vågledarstorlek eller vikt är viktiga överväganden.

En relativt ny teknik som används inuti ihåliga metall-vågledarfilter är finline, en sorts plan dielektrisk vågledare. Finline beskrevs första gången av Paul Meier 1972.

Multiplexer historik

John R. Pierce uppfann det korskopplade filtret och den sammanhängande passbandsmultiplexorn.

Multiplexer beskrevs först av Fano och Lawson 1948. Pierce var den första som beskrev multiplexorer med sammanhängande passband. Multiplexering med riktningsfilter uppfanns av Seymour Cohn och Frank Coale på 1950-talet. Multiplexrar med kompenserande immittansresonatorer vid varje korsning är till stor del ett verk av EG Cristal och GL Matthaei på 1960-talet. Denna teknik används fortfarande ibland, men den moderna tillgängligheten av datorkraft har lett till den vanligare användningen av syntestekniker som direkt kan producera matchande filter utan behov av dessa ytterligare resonatorer. 1965 upptäckte RJ Wenzel att filter som var enkelterminerade, ^[k] snarare än de vanliga dubbelterminerade, var komplementära – precis vad som behövdes för en diplexer. ^[c] Wenzel inspirerades av föreläsningarna av kretsteoretikern Ernst Guillemin .

Multi-channel, multi-oktav multiplexers undersöktes av Harold Schumacher vid Microphase Corporation, och hans resultat publicerades 1976. Principen att multiplexerfilter kan matchas när de sammanfogas genom att modifiera de första elementen, och därmed avskaffa de kompenserande resonatorerna , upptäcktes av misstag av EJ Curly runt 1968 när han felinställde en diplexer. En formell teori för detta tillhandahölls av JD Rhodes 1976 och generaliserades till multiplexorer av Rhodes och Ralph Levy 1979.

Från 1980-talet har plana teknologier, särskilt mikrostrip, tenderat att ersätta andra tekniker som används för att konstruera filter och multiplexorer, särskilt i produkter riktade till konsumentmarknaden. Den senaste innovationen av post-wall waveguide gör att vågledardesigner kan implementeras på ett plant substrat med billiga tillverkningstekniker liknande de som används för mikrostrip.

Komponenter

Figur 4. Stegkretsimplementering av ett lågpassfilter med klumpat element

Vågledarfilterkonstruktioner består ofta av två olika komponenter som upprepas ett antal gånger. Typiskt är en komponent en resonator eller diskontinuitet med en klumpad krets som motsvarar en induktor, kondensator eller LC-resonanskrets. Ofta kommer filtertypen att få sitt namn från stilen för den här komponenten. Dessa komponenter är åtskilda av en andra komponent, en styrlängd som fungerar som en impedanstransformator. Impedanstransformatorerna har den effekten att alternativa instanser av den första komponenten verkar ha en annan impedans. Nettoresultatet är en ekvivalent krets med klumpar i ett stegnätverk. Klumpade elementfilter är vanligtvis stegtopologi , och en sådan krets är en typisk utgångspunkt för vågledarfilterdesigner. Figur 4 visar en sådan stege. Vanligtvis är vågledarkomponenter resonatorer, och den ekvivalenta kretsen skulle vara LC-resonatorer istället för de visade kondensatorerna och induktorerna, men kretsar som figur 4 används fortfarande som prototypfilter med användning av en bandpass- eller bandstopptransformation.

Filterprestandaparametrar, såsom stoppbandsavvisning och övergångshastighet mellan passband och stoppband, förbättras genom att lägga till fler komponenter och därmed öka längden på filtret. Där komponenterna upprepas identiskt är filtret en bildparameterfilterdesign, och prestandan förbättras helt enkelt genom att lägga till fler identiska element. Detta tillvägagångssätt används vanligtvis i filterdesigner som använder ett stort antal tätt placerade element, såsom våffeljärnsfiltret . För konstruktioner där elementen är mer spridda kan bättre resultat erhållas med en nätverkssyntesfilterdesign, som det vanliga Chebyshev-filtret och Butterworth-filtren . I detta tillvägagångssätt har inte alla kretselementen samma värde, och följaktligen har komponenterna inte alla samma dimensioner. Dessutom, om designen förbättras genom att lägga till fler komponenter måste alla elementvärden beräknas igen från början. I allmänhet kommer det inte att finnas några gemensamma värden mellan de två instanserna av designen. Chebyshev vågledarfilter används där filtreringskraven är rigorösa, såsom satellitapplikationer.

Impedanstransformator

En impedanstransformator är en enhet som får en impedans vid dess utgångsport att framstå som en annan impedans vid dess ingångsport. I vågledare är denna enhet helt enkelt en kort vågledare. Särskilt användbar är kvartsvågsimpedanstransformatorn som har en längd på λ _g /4. Denna enhet kan omvandla kapacitanser till induktanser och vice versa. Den har också den användbara egenskapen att förvandla shuntkopplade element till seriekopplade element och vice versa. Seriekopplade element är annars svåra att implementera i vågledare.

Reflektioner och diskontinuiteter

Många vågledarfilterkomponenter fungerar genom att införa en plötslig förändring, en diskontinuitet, i vågledarens transmissionsegenskaper. Sådana diskontinuiteter är ekvivalenta med klumpade impedanselement placerade vid den punkten. Detta uppstår på följande sätt: diskontinuiteten orsakar en partiell reflektion av den utsända vågen tillbaka ner i guiden i motsatt riktning, varvid förhållandet mellan de två är känt som reflektionskoefficienten . Detta är helt analogt med en reflektion på en transmissionsledning där det finns ett etablerat samband mellan reflektionskoefficienten och impedansen som orsakade reflektionen. Denna impedans måste vara reaktiv , det vill säga den måste vara en kapacitans eller en induktans. Det kan inte vara ett motstånd eftersom ingen energi har absorberats – allt antingen sänds vidare eller reflekteras. Exempel på komponenter med den här funktionen inkluderar iris, stubbar och stolpar, alla beskrivs senare i den här artikeln under de filtertyper där de förekommer.

Impedanssteg

Ett impedanssteg är ett exempel på en anordning som introducerar en diskontinuitet. Det uppnås genom en stegvis förändring av vågledarens fysiska dimensioner. Detta resulterar i en stegvis förändring av den karakteristiska impedansen för vågledaren. Steget kan vara antingen i E-planet ^[f] (höjdförändring ^[j] ) eller H-planet ^[g] (förändring av bredd ^[i] ) hos vågledaren.

Resonant kavitetsfilter

Kavitetsresonator

En grundläggande komponent i vågledarfilter är kavitetsresonatorn . Denna består av en kort längd av vågledare blockerad i båda ändar. Vågor som fångas inuti resonatorn reflekteras fram och tillbaka mellan de två ändarna. En given kavitetsgeometri kommer att ge resonans vid en karakteristisk frekvens. Resonanseffekten kan användas för att selektivt passera vissa frekvenser. Deras användning i en filterstruktur kräver att en del av vågen tillåts passera ut ur en kavitet in i en annan genom en kopplingsstruktur. Men om öppningen i resonatorn hålls liten är ett giltigt konstruktionssätt att utforma kaviteten som om den vore helt stängd och felen kommer att vara minimala. Ett antal olika kopplingsmekanismer används i olika filterklasser.

Nomenklaturen för moder i en kavitet introducerar ett tredje index, till exempel TE ₀₁₁ . De två första indexen beskriver vågen som rör sig upp och ner längs kavitetens längd, det vill säga de är de tvärgående modtalen som för moder i en vågledare. Det tredje indexet beskriver den longitudinella moden som orsakas av interferensmönstret för de framåtgående och reflekterade vågorna. Det tredje indexet är lika med antalet halva våglängder längs med ledaren. De vanligaste moderna som används är de dominerande moderna: TE ₁₀₁ i rektangulär vågledare och TE ₁₁₁ i cirkulär vågledare. TE ₀₁₁ cirkulärt läge används där mycket låg förlust (därav hög Q ) krävs men kan inte användas i ett dubbellägesfilter eftersom det är cirkulärt symmetriskt. Bättre lägen för rektangulär vågledare i dual-mode filter är TE ₁₀₃ och TE ₁₀₅ . Ännu bättre är dock det cirkulära vågledarläget TE _{113 som kan uppnå ett} Q på 16 000 vid 12 GHz .

Stämskruv

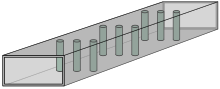
Stämskruvar är skruvar som sätts in i resonanshålrum som kan justeras externt till vågledaren. De ger finjustering av resonansfrekvensen genom att infoga mer eller mindre tråd i vågledaren. Exempel kan ses i postfiltret i figur 1: varje kavitet har en avstämningsskruv fäst med låsmuttrar och gänglåsande blandning . För skruvar som bara sätts in ett litet avstånd är motsvarande krets en shuntkondensator, som ökar i värde när skruven sätts in. Men när skruven har satts in ett avstånd λ/4 ger den resonans motsvarande en serie LC-krets. Att sätta in det ytterligare gör att impedansen ändras från kapacitiv till induktiv, det vill säga det aritmetiska tecknet ändras.

Iris

Figur 5. Vissa vågledaririsgeometrier och deras ekvivalenta kretsar med klumpar

En iris är en tunn metallplatta tvärs över vågledaren med ett eller flera hål i den. Den används för att koppla ihop två vågledare och är ett sätt att införa en diskontinuitet. Några av de möjliga geometrierna för iris visas i figur 5. En iris som minskar bredden på en rektangulär vågledare har en ekvivalent krets med en shuntinduktans, medan en som begränsar höjden är ekvivalent med en shuntkapacitans. En iris som begränsar båda riktningarna motsvarar en parallell LC-resonanskrets . En serie LC-krets kan bildas genom att placera den ledande delen av iris på avstånd från vågledarens väggar. Smalbandsfilter använder ofta iris med små hål. Dessa är alltid induktiva oavsett formen på hålet eller dess placering på iris. Cirkulära hål är enkla att bearbeta, men långsträckta hål, eller hål i form av ett kors, är fördelaktiga för att möjliggöra valet av ett speciellt kopplingssätt.

Iris är en form av diskontinuitet och fungerar med spännande försvinnande högre lägen. Vertikala kanter är parallella med det elektriska fältet (E-fältet) och exciterar TE-lägen. Den lagrade energin i TE-lägen är övervägande i magnetfältet (H-fältet), och följaktligen är den klumpade ekvivalenten av denna struktur en induktor. Horisontella kanter är parallella med H-fältet och exciterar TM-lägen. I detta fall är den lagrade energin övervägande i E-fältet och den klumpade ekvivalenten är en kondensator.

Det är ganska enkelt att göra iris som är mekaniskt justerbara. En tunn platta av metall kan tryckas in och ut ur ett smalt spår i sidan av vågledaren. Iriskonstruktionen väljs ibland för denna förmåga att göra en variabel komponent.

Iriskopplat filter

Figur 6. Iriskopplat filter med tre iris

Ett iriskopplat filter består av en kaskad av impedanstransformatorer i form av vågledarresonantkaviteter sammankopplade av iriser. I högeffektapplikationer undviks kapacitiva iris. Minskningen av vågledarens höjd (riktningen på E-fältet) gör att den elektriska fältstyrkan över gapet ökar och ljusbågsbildning (eller dielektriskt genombrott om vågledaren är fylld med en isolator) kommer att inträffa vid en lägre effekt än vad den annars skulle göra. .

Postfilter

Figur 7. Stolpfilter med tre rader stolpar

Stolpar är ledande stänger, vanligtvis cirkulära, fixerade internt över vågledarens höjd och är ett annat sätt att införa en diskontinuitet. En tunn stolpe har en motsvarande krets av en shuntinduktor. En rad med stolpar kan ses som en form av induktiv iris.

Ett stolpfilter består av flera rader av stolpar tvärs över vågledarens bredd som separerar vågledaren i resonanshåligheter som visas i figur 7. Olika antal stolpar kan användas i varje rad för att uppnå varierande induktansvärden. Ett exempel kan ses i figur 1. Filtret fungerar på samma sätt som det iriskopplade filtret men skiljer sig i konstruktionssätt.

Vågledare efter vägg

Huvudartikel: Post-wall waveguide

En vågledare efter vägg, eller substratintegrerad vågledare, är ett nyare format som försöker kombinera fördelarna med låg strålningsförlust, högt Q och hög effekthantering hos traditionella vågledare av ihåligt metallrör med den lilla storleken och enkla tillverkningen av plana vågledare. teknologier (som det mycket använda mikrostripformatet). Den består av ett isolerat substrat genomborrat med två rader av ledande stolpar som står in för vågledarens sidoväggar. Toppen och botten av substratet är täckta med ledande ark vilket gör detta till en liknande konstruktion som trippelformatet . De befintliga tillverkningsteknikerna för tryckta kretskort eller lågtemperatursameldad keramik kan användas för att tillverka vågledarkretsar efter vägg. Detta format lämpar sig naturligtvis för design av vågledarpostfilter.

Dual-mode filter

Ett dual-mode-filter är ett slags resonanshålighetsfilter, men i det här fallet används varje kavitet för att tillhandahålla två resonatorer genom att använda två moder (två polarisationer), så att filtrets volym halveras för en given ordning. Denna förbättring av filtrets storlek är en stor fördel i flygplans- och rymdtillämpningar. Högkvalitativa filter i dessa applikationer kan kräva många hålrum som upptar betydande utrymme.

Dielektriskt resonatorfilter

Figur 8. Dielektriskt resonatorfilter med tre tvärgående resonatorer

Dielektriska resonatorer är bitar av dielektriskt material som förs in i vågledaren. De är vanligtvis cylindriska eftersom dessa kan tillverkas utan bearbetning men andra former har använts. De kan göras med ett hål genom mitten som används för att fästa dem vid vågledaren. Det finns inget fält i mitten när TE ₀₁₁ cirkulärt läge används, så hålet har ingen negativ effekt. Resonatorerna kan monteras koaxiellt mot vågledaren, men vanligtvis monteras de tvärs över bredden som visas i figur 8. Det senare arrangemanget gör att resonatorerna kan avstämmas genom att föra in en skruv genom vågledarens vägg i mitthålet på resonator.

När dielektriska resonatorer är gjorda av ett material med hög permittivitet , såsom ett av bariumtitanaten, har de en viktig platsbesparande fördel jämfört med kavitetsresonatorer. Men de är mycket mer benägna att använda falska lägen. I högeffektapplikationer kan metallskikt byggas in i resonatorerna för att leda bort värme eftersom dielektriska material tenderar att ha låg värmeledningsförmåga .

Resonatorerna kan kopplas ihop med iris eller impedanstransformatorer. Alternativt kan de placeras i ett stubbliknande sidohus och kopplas genom en liten öppning.

Sätt i filter

Figur 9. Sätt i filter med sex dielektriska resonatorer i E-planet.

I insatsfilter placeras en eller flera metallplåtar längs med vågledarens längd som visas i figur 9. Dessa plåtar har hål i dem för att bilda resonatorer. Luftdielektriken ger dessa resonatorer ett högt Q . Flera parallella skär kan användas i samma längd av vågledaren. metallplåt till priset av en lägre resonator Q.

Finline filter

Finline är en annan typ av vågledarteknik där vågor i en tunn remsa av dielektrikum begränsas av två metalliseringsremsor. Det finns ett antal möjliga topologiska arrangemang av de dielektriska banden och metallremsorna. Finline är en variant av slot-waveguide men i fallet med finline är hela strukturen innesluten i en metallsköld. Detta har fördelen att, liksom ihålig metallvågledare, ingen effekt går förlorad av strålning. Finline-filter kan tillverkas genom att skriva ut ett metalliseringsmönster på ett ark av dielektriskt material och sedan föra in arket i E-planet av en ihålig metallvågledare ungefär som man gör med insatsfilter. Metallvågledaren bildar skölden för finlinevågledaren. Resonatorer bildas genom att metallisera ett mönster på det dielektriska arket. Mer komplexa mönster än det enkla insticksfiltret i figur 9 uppnås lätt eftersom konstruktören inte behöver ta hänsyn till effekten på det mekaniska stödet av att ta bort metall. Denna komplexitet ökar inte tillverkningskostnaderna eftersom antalet processer som behövs inte ändras när fler element läggs till designen. Finline-designer är mindre känsliga för tillverkningstoleranser än insatsfilter och har breda bandbredder.

Evanescent-läge filter

Det är möjligt att designa filter som fungerar internt helt i flyktiga lägen. Detta har utrymmesbesparande fördelar eftersom filtervågledaren, som ofta utgör filtrets hölje, inte behöver vara tillräckligt stor för att stödja utbredning av den dominerande moden. Typiskt består ett evanescent-modfilter av en vågledare som är mindre än den vågledare som matar in- och utgångsportarna. I vissa utföranden kan detta vara vikt för att uppnå ett mer kompakt filter. Stämskruvar sätts in med specifika intervall längs vågledaren, vilket ger likvärdiga klumpade kapacitanser vid dessa punkter. I nyare konstruktioner ersätts skruvarna med dielektriska insatser. Dessa kondensatorer resonerar med den föregående längden av evanescent-modvågledaren som har den ekvivalenta kretsen som en induktor, vilket sålunda alstrar en filtreringsverkan. Energi från många olika evanescenta lägen lagras i fältet runt var och en av dessa kapacitiva diskontinuiteter. Emellertid är designen sådan att endast det dominerande läget når utgångsporten; de andra lägena sönderfaller mycket snabbare mellan kondensatorerna.

Korrugerat vågledarfilter

Figur 10. Korrugerat vågledarfilter med utskärning som visar korrugeringarna inuti

Figur 11. Längdsnitt genom ett vågledarfilter

Korrugerade vågledarfilter , även kallade åsade vågledarfilter , består av ett antal åsar, eller tänder, som periodiskt reducerar vågledarens inre höjd som visas i figurerna 10 och 11. De används i applikationer som samtidigt kräver ett brett passband , bra passbandsmatchning och ett brett stoppband. De är i huvudsak lågpassdesigner (över den vanliga begränsningen av cutoff-frekvensen), till skillnad från de flesta andra former som vanligtvis är bandpass. Avståndet mellan tänderna är mycket mindre än det typiska λ/4-avståndet mellan element i andra filterkonstruktioner. Vanligtvis är de designade med bildparametermetoden med alla åsar identiska, men andra filterklasser som Chebyshev kan uppnås i utbyte mot komplexiteten i tillverkningen. I bilddesignmetoden modelleras den ekvivalenta kretsen av åsarna som en kaskad av LC-halvsektioner . Filtret fungerar i det dominerande TE ₁₀ -läget, men falska lägen kan vara ett problem när de finns. I synnerhet finns det liten stoppbandsdämpning av TE _20- och TE ₃₀ -lägena.

Våffeljärnsfilter

Huvudartikel: våffeljärnsfilter

Våffeljärnsfiltret är en variant av vågledarfiltret. Det har liknande egenskaper som det filtret med den ytterligare fördelen att falska TE _20- och TE ₃₀ -moder undertrycks. I våffeljärnsfiltret skärs kanaler genom åsarna längsgående ner i filtret. Detta lämnar en matris av tänder som sticker ut internt från vågledarens övre och undre ytor. Detta tandmönster liknar ett våffeljärn , därav namnet på filtret.

Vågledare stubbfilter

Figur 12. Vågledarstumfilter bestående av tre stubbresonatorer

En stubb är en kort vågledare som är ansluten till någon punkt i filtret i ena änden och kortsluten i den andra änden. Öppna kretsar är också teoretiskt möjliga, men en implementering i vågledare är inte praktisk eftersom elektromagnetisk energi skulle sändas ut från den öppna änden av stubben, vilket resulterar i stora förluster. Stubbar är en sorts resonator, och ekvivalenten med klumpat element är en LC-resonanskrets. Men över ett smalt band kan stubbar ses som en impedanstransformator. Kortslutningen omvandlas till antingen en induktans eller en kapacitans beroende på stubbens längd.

Ett vågledarstubbsfilter görs genom att placera en eller flera stubbar längs med en vågledares längd, vanligtvis λ _g /4 från varandra, som visas i figur 12. Ändarna på stubbarna är avskärmade för att kortsluta dem. När de kortslutna stubbarna är λ _g /4 långa kommer filtret att vara ett bandstoppfilter och stubbarna kommer att ha en ungefärlig ekvivalent krets med klumpade element av parallella resonanskretsar kopplade i serie med ledningen. När stubbarna är λ _g /2 långa kommer filtret att vara ett bandpassfilter . I detta fall är ekvivalenten med klumpelementen serie LC-resonanskretsar i serie med linjen.

Absorptionsfilter

Absorptionsfilter avleder energin i oönskade frekvenser internt som värme. Detta i motsats till en konventionell filterdesign där de oönskade frekvenserna reflekteras tillbaka från filtrets ingångsport. Sådana filter används där det inte är önskvärt att ström skickas tillbaka mot källan. Detta är fallet med högeffektssändare där retureffekten kan vara tillräckligt hög för att skada sändaren. Ett absorptionsfilter kan användas för att ta bort sändarens falska emissioner såsom övertoner eller falska sidband . En design som har använts en tid har slitsar i väggarna på matningsvågledaren med jämna mellanrum. Denna design är känd som ett läckande vågfilter . Varje slits är ansluten till en mindre vågledare som är för liten för att stödja utbredning av frekvenser i det önskade bandet. Således är dessa frekvenser opåverkade av filtret. Högre frekvenser i det oönskade bandet utbreder sig dock lätt längs sidostyrningarna som avslutas med en anpassad belastning där kraften absorberas. Dessa laster är vanligtvis en kilformad bit av mikrovågsabsorberande material. En annan, mer kompakt design av absorptionsfilter använder resonatorer med en förlustgivande dielektrikum.

Filterliknande enheter

Det finns många tillämpningar av filter vars designmål är något annat än avvisande eller överföring av vissa frekvenser. Ofta kommer en enkel enhet som är avsedd att arbeta över endast ett smalt band eller bara en punktfrekvens inte att se mycket ut som en filterdesign. En bredbandsdesign för samma objekt kräver dock många fler element och designen får karaktären av ett filter. Bland de vanligare applikationerna av detta slag i vågledare är impedansmatchande nätverk, riktningskopplare, effektdelare, effektkombinerare och diplexrar . Andra möjliga tillämpningar inkluderar multiplexorer , demultiplexrar, negativa resistansförstärkare och tidsfördröjningsnätverk .

Impedansmatchning

Figur 13 . En ortomodgivare (en mängd olika duplexorer ) som innehåller stegvis impedansmatchning

En enkel metod för impedansmatchning är stubbmatchning med en enda stubb. En enda stubb kommer dock bara att producera en perfekt matchning vid en viss frekvens. Denna teknik är därför endast lämplig för smalbandsapplikationer. För att bredda bandbredden kan flera stubbar användas, och strukturen tar då formen av ett stubbfilter. Designen fortsätter som om det vore ett filter förutom att en annan parameter är optimerad. I ett frekvensfilter är den parameter som optimeras typiskt stoppbandsavvisning, passbandsdämpning, brant övergång eller någon kompromiss mellan dessa. I ett matchande nätverk är den optimerade parametern impedansmatchningen. Enhetens funktion kräver ingen begränsning av bandbredd, men designern tvingas ändå välja en bandbredd på grund av enhetens struktur .

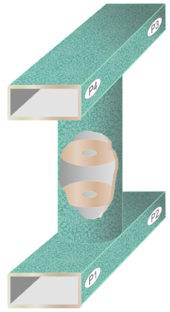
Stubbar är inte det enda filterformatet som kan användas. I princip kan vilken filterstruktur som helst användas för impedansmatchning, men vissa kommer att resultera i mer praktiska konstruktioner än andra. Ett frekvent format som används för impedansmatchning i vågledare är stegimpedansfiltret. Ett exempel kan ses i duplexenheten ^[e] på bilden i figur 13.

Riktningskopplare och kraftkombinatorer

Figur 14. En vågledarkopplare med flera hål

Riktkopplare, effektdelare och kraftkombinatorer är alla i huvudsak samma typ av enhet, åtminstone när de implementeras med passiva komponenter. En riktningskopplare delar en liten mängd ström från huvudledningen till en tredje port. En starkare kopplad, men i övrigt identisk, enhet kan kallas en kraftdelare. En som kopplar exakt hälften av strömmen till den tredje porten (en 3 dB- kopplare) är den maximala kopplingen som kan uppnås utan att vända portarnas funktioner. Många konstruktioner av kraftdelare kan användas omvänt, varpå de blir kraftkombinatorer.

En enkel form av riktningskopplare är två parallella transmissionsledningar som är sammankopplade över en längd A/4. Denna design är begränsad eftersom den elektriska längden på kopplaren endast kommer att vara λ/4 vid en specifik frekvens. Kopplingen kommer att vara maximal vid denna frekvens och faller bort på vardera sidan. I likhet med impedansmatchningsfallet kan detta förbättras genom att använda flera element, vilket resulterar i en filterliknande struktur. En vågledaranalog till detta kopplade linjers tillvägagångssätt är Bethe-hole riktningskopplaren i vilken två parallella vågledare är staplade ovanpå varandra och ett hål tillhandahålls för koppling. För att producera en bredbandsdesign används flera hål längs styrningarna som visas i figur 14 och en filterdesign tillämpas. Det är inte bara den kopplade linjedesignen som lider av att vara smalbandig, alla enkla konstruktioner av vågledarkopplare beror på frekvensen på något sätt. Till exempel råttracekopplaren (som kan implementeras direkt i vågledaren) på en helt annan princip men förlitar sig fortfarande på att vissa längder är exakta i termer av λ.

Diplexer och duplexer

En diplexer är en enhet som används för att kombinera två signaler som upptar olika frekvensband till en enda signal. Detta är vanligtvis för att möjliggöra att två signaler sänds samtidigt på samma kommunikationskanal, eller för att tillåta sändning på en frekvens medan mottagning på en annan. (Denna specifika användning av en diplexer kallas en duplexer.) Samma enhet kan användas för att separera signalerna igen längst ut på kanalen. Behovet av filtrering för att separera signalerna under mottagning är ganska självklart men det krävs också även när två sända signaler kombineras. Utan filtrering kommer en del av kraften från källa A att skickas mot källa B istället för den kombinerade utsignalen. Detta kommer att ha de skadliga effekterna att förlora en del av ineffekten och belastningskällan A med utgångsimpedansen från källan B, vilket sålunda orsakar missanpassning. Dessa problem skulle kunna övervinnas med användningen av en 3 dB riktkopplare, men som förklarats i föregående avsnitt kräver en bredbandsdesign en filterdesign för riktningskopplare också.

Två smalbandiga signaler med stort avstånd kan diplexeras genom att sammanfoga utgångarna från två lämpliga bandpassfilter. Åtgärder måste vidtas för att förhindra att filtren kopplas till varandra när de är i resonans vilket skulle orsaka försämring av deras prestanda. Detta kan uppnås med lämpligt avstånd. Om t.ex. filtren är av den iriskopplade typen placeras irisen närmast filterövergången för filter A λ _gb /4 från korsningen där λ _gb är styrvåglängden i passbandet för filter B. På samma sätt, närmaste iris av filter B placeras λ _ga /4 från korsningen. Detta fungerar eftersom när filter A är i resonans är filter B i sitt stoppband och endast löst kopplat och vice versa. Ett alternativt arrangemang är att ha varje filter sammanfogat med en huvudvågledare vid separata korsningar. En frånkopplingsresonator placeras λg _/ 4 från förbindelsen mellan varje filter. Detta kan vara i form av en kortsluten stubb som är avstämd till filtrets resonansfrekvens. Detta arrangemang kan utökas till multiplexorer med valfritt antal band.

För diplexrar som hanterar sammanhängande passband måste korrekt hänsyn tas till filterkorsningsegenskaperna i konstruktionen. Ett särskilt vanligt fall av detta är när diplexern används för att dela upp hela spektrumet i låga och höga band. Här används ett lågpass- och ett högpassfilter istället för bandpassfilter. Syntesteknikerna som används här kan likaväl tillämpas på smalbandsmultiplexorer och eliminerar till stor del behovet av avkopplingsresonatorer.

Riktningsfilter

Figur 15 . Ett vågledarriktfilter skär bort för att visa de cirkulära vågledaririsarna

Ett riktningsfilter är en enhet som kombinerar funktionerna hos en riktningskopplare och en diplexer. Eftersom den är baserad på en riktningskopplare är den i huvudsak en enhet med fyra portar, men liksom riktningskopplare är port 4 vanligtvis permanent avslutad internt. Ström som går in i port 1 lämnar port 3 efter att ha varit föremål för någon filtreringsfunktion (vanligtvis bandpass). Den återstående kraften lämnar port 2, och eftersom ingen effekt absorberas eller reflekteras kommer detta att vara det exakta komplementet till filtreringsfunktionen vid port 2, i detta fall bandstopp. Omvänt kombineras kraften som går in i portarna 2 och 3 vid port 1, men nu absorberas effekten från signalerna som avvisas av filtret i belastningen vid port 4. Figur 15 visar en möjlig vågledarimplementering av ett riktat filter. Två rektangulära vågledare som arbetar i den dominerande TE ₁₀ -moden tillhandahåller de fyra portarna. Dessa är sammanfogade av en cirkulär vågledare som arbetar i den cirkulära TE ₁₁ -moden. Den cirkulära vågledaren innehåller ett iriskopplat filter med så många iriser som behövs för att producera det erforderliga filtersvaret.

Ordlista

^ bländare

En öppning i en vägg av en vågledare eller barriär mellan sektioner av vågledaren genom vilken elektromagnetisk strålning kan fortplanta sig.

^ ^{a b} karakteristisk impedans

₀ Karakteristisk impedans , symbol Z , för en vågledare för en viss mod definieras som förhållandet mellan det transversella elektriska fältet och det transversella magnetfältet för en våg som rör sig i en riktning nedför ledaren. Den karakteristiska impedansen för luftfylld vågledare ges av,

${\displaystyle Z_{0}=\left\{{\begin{matrix} Z_{\mathrm {f} }{\dfrac {\lambda _{\mathrm {g} }}{\lambda }}&{\text{(TE-läge)}}\\\\Z_{\mathrm {f} }{\dfrac {\lambda }{\lambda _{\mathrm {g} }}}&{\text{(TM-läge)}}\end{matris}}\right.} där Z$

f är _impedansen för fri space , ungefär 377 Ω , λ _g är guidevåglängden och λ är våglängden när den inte begränsas av guiden. För en dielektriskt fylld vågledare måste uttrycket delas med √ κ , där κ är materialets dielektriska konstant, och λ ersättas med den obegränsade våglängden i det dielektriska mediet. I vissa behandlingar kallas det som här kallas karakteristisk impedans för vågimpedansen, och karakteristisk impedans definieras som proportionell mot den av någon konstant.

^ ^{c d e} diplexer, duplexer

En diplexer kombinerar eller separerar två signaler som upptar olika passband. En duplexer kombinerar eller delar två signaler som rör sig i motsatta riktningar, eller av olika polarisationer (som också kan vara i olika passband).

^ E-plan

E-planet är det plan som ligger i det tvärgående elektriska fältets riktning, det vill säga vertikalt längs styrningen.

^ styrvåglängd

Styrvåglängd, symbol λ _g , är våglängden mätt i längdriktningen nedför vågledaren. För en given frekvens beror λ _g på överföringssättet och är alltid längre än våglängden för en elektromagnetisk våg med samma frekvens i det fria rymden. λ _g är relaterad till gränsfrekvensen, f _c , by,

$\lambda _{\mathrm {g} }={\frac {\lambda }{\sqrt {1-\left({\frac {f_{\mathrm {c} }}{f}}\right)^{2}}}}$

där λ är våglängden som vågen skulle ha om den inte begränsas av guiden. För ledare som endast är fyllda med luft kommer detta att vara detsamma, för alla praktiska ändamål, som den fria rymdvåglängden för den sända frekvensen, f .

^ H-plan

H-planet är det plan som ligger i det tvärgående magnetfältets riktning ( H är analyssymbolen för magnetfältets styrka ), det vill säga horisontellt längs guiden.

^ ^{i j} höjd, bredd

För en rektangulär styrning hänvisar dessa till de små och stora inre dimensionerna av dess tvärsnitt. Polariseringen av E-fältet för den dominerande moden är parallell med höjden.

^ iris

En ledande platta passad tvärs över vågledaren med en, vanligtvis stor, öppning.

^ enkelterminerad, dubbelterminerad

Ett dubbelterminerat filter (normalfallet) är ett där generatorn och lasten, anslutna till ingångs- respektive utgångsportarna, har impedanser som matchar filtrets karakteristiska impedans. Ett enkelt avslutat filter har en matchande belastning, men drivs antingen av en lågimpedansspänningskälla eller en högimpedansströmkälla.

^ TEM-läge

Tvärgående elektromagnetiskt läge, ett transmissionsläge där allt elektriskt fält och allt magnetfält är vinkelräta mot den elektromagnetiska vågens färdriktning. Detta är det vanliga överföringssättet i par av ledare.

^ TE-läge

Tvärgående elektriskt läge, ett av ett antal lägen där allt elektriskt fält, men inte allt magnetfält, är vinkelrät mot den elektromagnetiska vågens färdriktning. De betecknas H-lägen i vissa källor eftersom dessa lägen har en longitudinell magnetisk komponent. Det första indexet indikerar antalet halva våglängder av fältet över vågledarens bredd, och det andra indexet indikerar antalet halva våglängder över höjden. Egentligen bör indexen separeras med ett kommatecken, men vanligtvis körs de tillsammans, eftersom lägesnummer i dubbelsiffriga sällan behöver beaktas. Några lägen som specifikt nämns i den här artikeln listas nedan. Alla lägen är för rektangulär vågledare om inget annat anges.

           ^ TE ₀₁ -läge

Ett läge med en halvvåg av elektriskt fält över guidens höjd och enhetligt elektriskt fält (noll halvvågor) över guidens bredd.

           ^ TE _10- läge

Ett läge med en halvvåg av elektriskt fält över guidens bredd och enhetligt elektriskt fält över guidens höjd.

           ^ TE ₂₀ -läge

Ett läge med två halvvågor av elektriskt fält över guidens bredd och enhetligt elektriskt fält över guidens höjd.

           ^ TE ₁₁ cirkulärt läge

Ett läge med en helvåg av elektriskt fält runt omkretsen av guiden och en halvvåg av elektriskt fält längs en radie.

^ TM-läge

Tvärgående magnetiskt läge, ett av ett antal lägen där allt magnetfält, men inte allt elektriskt fält, är vinkelrät mot den elektromagnetiska vågens färdriktning. De betecknas E-lägen i vissa källor eftersom dessa lägen har en längsgående elektrisk komponent. Se TE-läge för en beskrivning av betydelsen av indexen. Några lägen som specifikt nämns i den här artikeln är:

           ^ TM ₁₁ -läge

Ett läge med en halvvåg av magnetfält över guidens bredd och en halvvåg av magnetfält över guidens höjd. Detta är det lägsta TM-läget, eftersom TM _{m 0} -lägen inte kan existera.

           ^ TM ₀₁ cirkulärt läge

Ett läge med enhetligt magnetfält runt omkretsen av guiden och en halvvåg av magnetfält längs en radie.

^ ^{o p} transmissionsledning

En transmissionsledning är ett signalöverföringsmedium som består av ett par elektriska ledare separerade från varandra, eller en ledare och en gemensam returväg. I vissa behandlingar anses vågledare vara inom klassen överföringsledningar, som de har mycket gemensamt med. I denna artikel ingår inte vågledare så att de två typerna av medium lättare kan särskiljas och refereras.

Bibliografi

•   Bagad, VS, Microwave Engineering , Technical Publications Pune, 2009 ISBN 81-8431-360-8 .
•   Belov, Leonid A.; Smolskiy, Sergey M.; Kochemasov, Victor N., Handbook of RF, Microwave, and Millimeter-wave Components , Artech House, 2012 ISBN 1-60807-209-6 .
•   Bowen, Edward George, A Textbook of Radar , Cambridge University Press, 1954 OCLC 216292853 .
•   Bray, John, Innovation and the Communications Revolution: From the Victorian Pioneers to Broadband Internet , IEE, 2002 ISBN 0-85296-218-5 .
•   Cauer, E.; Mathis W.; Pauli, R., "Life and Work of Wilhelm Cauer (1900 – 1945)" , Proceedings of the Fourteenth International Symposium of Mathematical Theory of Networks and Systems (MTNS2000), Perpignan, juni, 2000 OCLC 65290907 .
•   Connor, FR, Wave Transmission , Edward Arnold Ltd., 1972 ISBN 0-7131-3278-7 .
• Cohn, SB, "Mikrovågsfilter som innehåller dielektriska resonatorer med hög Q " , G-MTT Symposium Digest, sidorna 49–50, 5–7 maj 1965.
• Cristal, Edward G., "Analytisk lösning på en vågledares läckande vågfilterstruktur", IEEE Transactions on Microwave Theory and Techniques , volym 11, nummer 3, sidorna 182–190, 1963.
• Cristal, Edward G.; Matthaei, GL, "En teknik för design av multiplexorer med sammanhängande kanaler", IEEE Transactions on Microwave Theory and Techniques , volym 12, nummer 1, sidorna 88–93, 1964.
•   Das, Annapurna; Das, Sisir K, Microwave Engineering , Tata McGraw-Hill Education, 2009 ISBN 0-07-066738-1 .
•   Elmore, William Cronk; Heald, Mark Aiken, Physics of Waves , Courier Dover Publications, 1969 ISBN 0-486-14065-2 .
•   Eskelinen, Harri; Eskelinen, Pekka, Microwave Component Mechanics , Artech House, 2003 ISBN 1-58053-589-5 .
•   Fano, RM; Lawson, AW, "Design of microwave filters", kapitel 10 i Ragan, GL (red.), Microwave Transmission Circuits , McGraw-Hill, 1948 OCLC 2205252 .
•   Gibilisco, Stan; Sclater, Neil, Encyclopedia of Electronics , Tab Professional and Reference Books, 1990 ISBN 0-8306-3389-8 .
•   Golio, Mike, Commercial Wireless Circuits and Components Handbook , CRC Press, 2002 ISBN 1-4200-3996-2 .
• Griffin, EL; Young, FA, "En jämförelse av fyra övermoderade kanoniska smala bandpassfilter vid 12 GHz" , Microwave Symposium Digest, 1978 IEEE-MTT-S International , sidorna 47–49.
• Gusmano, G.; Bianco, A.; Viticoli, M.; Kaciulis, S.; Mattogno, G.; Pandolfi, L., "Studie av Zr _1−x Sn _x TiO ₄ tunna filmer framställda genom en polymer prekursorrutt" , Surface and Interface Analysis , volym 34, nummer 1, sidorna 690–693, augusti 2002.
•   Hitchcock, R. Timothy; Patterson, Robert M., Radio-Frequency and ELF Electromagnetic Energies: A Handbook for Health Professionals , John Wiley & Sons, 1995 ISBN 0-471-28454-8 .
•   Hunter, IC, Teori och design av mikrovågsfilter , IET, 2001 ISBN 0-85296-777-2 .
•   Huurdeman, Anton A., The Worldwide History of Telecommunications , Wiley-IEEE, 2003 ISBN 0-471-20505-2 .
•   Ishii, Thomas Koryu, Handbook of Microwave Technology: Components and devices , Academic Press, 1995 ISBN 0-12-374696-5 .
•   Jarry, Pierre; Beneat, Jacques, Design and Realizations of Miniaturized Fractal Microwave and RF Filters , John Wiley & Sons, 2009 ISBN 0-470-48781-X .
•   Ke, Wu; Lei, Zhu; Vahldieck, Ruediger, "Mikrovågs passiva komponenter", i Chen, Wai-Kei (red.), The Electrical Engineering Handbook , Academic Press, 2004 ISBN 0-08-047748-8 .
•   Lee, Thomas H., Planar Microwave Engineering , sidorna 585–618, Cambridge University Press, 2004 ISBN 0-521-83526-7 .
• Levy, R.; Cohn, SB, "A History of microwave filter research, design and development" , IEEE Transactions: Microwave Theory and Techniques , sidorna 1055–1067, volym 32, nummer 9, 1984.
•   Mahmoud, SF, Electromagnetic waveguides: Theory and Applications , IEE, 1991 ISBN 0-86341-232-7 .
•   Maloratsky, Leo G., Integrated Microwave Front-ends with Avionics Applications , Artech House, 2012 ISBN 1-60807-206-1 .
•   Mansour, RR, "Tredimensionella kryogena filter" i H. Weinstock, H.; Nisenoff, M., Microwave Superconductivity , sidorna 161–188, Springer, 2001 ISBN 1-4020-0445-1 .
• Mason, WP; Sykes, RA "Användningen av koaxiala och balanserade transmissionslinjer i filter och bredbandstransformatorer för höga radiofrekvenser", Bell System Technical Journal , sidorna 275–302, volym 16, 1937.
• Massé, DJ; Pucel, RA, "Ett temperaturstabilt bandpassfilter som använder dielektriska resonatorer" , Proceedings of the IEEE , volym 60, nummer 6, sidorna 730–731, juni 1972.
•   Matthaei, George L.; Young, Leo; Jones, EMT, mikrovågsfilter, impedansmatchande nätverk och kopplingsstrukturer , McGraw-Hill, 1964 LCCN 64-7937 .
• Meier, Paul J., "Två nya integrerade kretsmedier med speciella fördelar vid millimetervåglängder", 1972 IEEE GMTT International Microwave Symposium , sidorna 221–223, 22–24 maj 1972.
•   Meredith, Roger, Engineers' Handbook of Industrial Microwave Heating , IET, 1998 ISBN 0-85296-916-3 .
•   Middleton, Wendy M.; Van Valkenburg, Mac Elwyn, Referensdata för ingenjörer: radio, elektronik, datorer och kommunikation , Newnes, 2002 ISBN 0-7506-7291-9 .
•   Millman, S. (red.), A History of Engineering and Science in the Bell System: Communications Sciences (1925–1980), AT&T Bell Laboratories, 1984 ISBN 0-932764-06-1 .
• Minakova, LB; Rud, LA, "Natural-frequency approach to the synthesis of narrow-band waveguide absorption filters", 32 :a Europeiska mikrovågskonferensen, 2002 , 23–26 september 2002, Milano.
•   Montgomery, Carol Gray; Dicke, Robert Henry; Purcell, Edward M., Principles of Microwave Circuits , IEE, 1948 ISBN 0-86341-100-2 .
•   Nalwa, Hari Singh (red), Handbook of Low and High Dielectric Constant Materials and their Applications , Academic Press, 1999 ISBN 0-08-053353-1 .
• Pierce, JR, "Paralleled-resonator filters" , Proceedings of the IRE, volym 37, sidorna 152–155, februari 1949.
•   Radmanesh, Matthew M., Advanced RF and Microwave Circuit Design , AuthorHouse, 2009 ISBN 1-4259-7244-6 .
• Rhodes, JD, "Direct design of symmetrical interacting bandpass channel diplexers" , IEE Journal on Microwaves, Optics and Acoustics , volym 1, nummer 1, sidorna 34–40, september 1976.
• Rhodes, JD; Levy, R., "A generalized multiplexer theory" , IEEE Transactions on Microwave Theory and Techniques , volym 27, nummer 2, sidorna 99–111, februari 1979.
• Richards, Paul I., "Resistor-transmission-line circuits" , Proceedings of the IRE , volym 36, sidorna 217–220, februari 1948.
•   Russer, Peter, Elektromagnetik, mikrovågskretsar och antenndesign för kommunikationsteknik, Artech House, 2003 ISBN 1-58053-532-1 .
•   Sarkar, TK ; Mailloux, Robert; Oliner, Arthur A .; Salazar-Palma, M.; Sengupta Dipak L., History of Wireless , John Wiley & Sons, 2006 ISBN 0-471-78301-3 .
•   Schumacher, HL, "Coax multiplexers: key to EW signal sorting", Microwave Systems News , sidorna 89–93, augusti/september 1976 ISSN 0164-3371
•   Silver, Samuel, Mikrovågsantennteori och design , IEE, 1949 ISBN 0-86341-017-0 .
•   Sorrentino, Roberto; Bianchi, Giovanni, Microwave and RF Engineering , John Wiley & Sons, 2010 ISBN 0-470-66021-X .
•   Srivastava, Ganesh Prasad; Gupta, Vijay Laxmi, Microwave Devices and Circuit Designs , Prentice-Hall of India, 2006 ISBN 81-203-2195-2 .
•   Waterhouse, Rod, Microstrip Patch Antennas: A Designer's Guide , Springer, 2003 ISBN 1-4020-7373-9 .
• Wenzel, JR, "Tillämpning av exakta syntesmetoder för flerkanalig filterdesign", IEEE Transactions on Microwave Theory and Techniques , volym 13, nummer 1, sidorna 5–15, januari 1965.
•   Xuan, Hu Wu; Kishk, Ahmed A., Analys och design av substratintegrerad vågledare med effektiv 2D-hybridmetod, Morgan & Claypool, 2010 ISBN 1-59829-902-6 .
•   Ja, C.; Shimabukuro, FI, The Essence of Dielectric Waveguides , Springer, 2008 ISBN 0-387-49799-4 .
• Young, L., "Direktkopplade kavitetsfilter för breda och smala bandbredder", IEEE Transactions: Microwave Theory and Techniques , volym MTT-11, sidorna 162–178, maj 1963.
• Young, Soo Lee; Getsinger, WJ; Sparrow, LR, "Barium tetratitanate MIC technology" , IEEE Transactions on Microwave Theory and Techniques , volym 27, nummer 7, sidorna 655–660, juli 1979.
• Zhang, Xianrong; Wang, Qingyuan; Li, Hong; Liu, Rongjun, "Evanescent mode compact waveguide filter" , International Conference on Microwave and Millimeter Wave Technology, 2008 (ICMMT 2008), volym 1, sidorna 323–325, IEEE, 2008.