Elektronisk filtertopologi

En elementär filtertopologi introducerar en kondensator i återkopplingsvägen för en op-förstärkare för att uppnå en obalanserad aktiv implementering av en lågpassöverföringsfunktion

Elektronisk filtertopologi definierar elektroniska filterkretsar utan att notera värdena på de komponenter som används utan endast sättet på vilket dessa komponenter är anslutna.

Filterdesign kännetecknar filterkretsar främst genom deras överföringsfunktion snarare än deras topologi . Överföringsfunktioner kan vara linjära eller olinjära . Vanliga typer av linjär filteröverföringsfunktion är; högpass , lågpass , bandpass , bandavvisande eller notch and all-pass . När överföringsfunktionen för ett filter har valts, kan den speciella topologin för att implementera ett sådant prototypfilter väljas så att man till exempel kan välja att designa ett Butterworth-filter med Sallen–Key-topologin .

Filtertopologier kan delas in i passiva och aktiva typer. Passiva topologier består uteslutande av passiva komponenter : motstånd, kondensatorer och induktorer. Aktiva topologier inkluderar också aktiva komponenter (som transistorer, op-förstärkare och andra integrerade kretsar) som kräver ström. Vidare kan topologier implementeras antingen i obalanserad form eller i balanserad form när de används i balanserade kretsar . Implementeringar som elektroniska mixers och stereoljud kan kräva uppsättningar av identiska kretsar.

Passiva topologier

Passiva filter har varit länge under utveckling och användning . De flesta är byggda från enkla tvåportsnätverk som kallas "sektioner". Det finns ingen formell definition av en sektion förutom att den måste ha minst en seriekomponent och en shuntkomponent. Sektioner är undantagslöst sammankopplade i en "kaskad" - eller "daisy-chain" -topologi, bestående av ytterligare kopior av samma sektion eller av helt olika sektioner. Reglerna för serie- och parallellimpedans skulle kombinera två sektioner som endast består av seriekomponenter eller shuntkomponenter till en enda sektion.

Vissa passiva filter, som endast består av en eller två filtersektioner, ges speciella namn, inklusive L-sektionen, T-sektionen och Π-sektionen, som är obalanserade filter, och C-sektionen, H-sektionen och box-sektionen, som är balanserade. Alla är byggda på en mycket enkel "stege"-topologi (se nedan). Diagrammet längst ner på sidan visar dessa olika topologier i termer av generella konstanta k-filter .

Filter designade med hjälp av nätverkssyntes upprepar vanligtvis den enklaste formen av L-sektionstopologi även om komponentvärden kan ändras i varje sektion. Bilddesignade filter , å andra sidan, behåller samma grundläggande komponentvärden från sektion till sektion även om topologin kan variera och tenderar att använda mer komplexa sektioner.

L-sektioner är aldrig symmetriska utan två L-sektioner rygg mot rygg bildar en symmetrisk topologi och många andra sektioner har symmetriska form.

Stegtopologier

Stegtopologi, ofta kallad Cauer-topologi efter Wilhelm Cauer (uppfinnaren av det elliptiska filtret ), användes faktiskt först av George Campbell (uppfinnaren av konstant k-filtret ). Campbell publicerades 1922 men hade uppenbarligen använt topologin en tid innan detta. Cauer tog först upp på stegar (publicerad 1926) inspirerad av Fosters arbete (1924). Det finns två former av grundläggande stegtopologier: obalanserad och balanserad. Cauer-topologi brukar betraktas som en obalanserad stegtopologi.

Ett stegnätverk består av kaskadformade asymmetriska L-sektioner (obalanserade) eller C-sektioner (balanserade). I lågpassform skulle topologin bestå av serieinduktorer och shuntkondensatorer. Andra bandformer skulle ha en lika enkel topologi transformerad från lågpass-topologin. Det transformerade nätet kommer att ha shuntadmittanser som är dubbla nät av serieimpedanserna om de var dubbla i startnätet - vilket är fallet med serieinduktorer och shuntkondensatorer.

Bildfiltersektioner _

Obalanserad
L Halvsektion	T-sektion	Π Sektion

Stegnätverk

Balanserad
C Halvsektion	H sektion		Box Sektion

Stegnätverk

X-sektion (mid-T-härledd)		X-sektion (mitten-Π-härledd)

OBS!	Läroböcker och designritningar visar vanligtvis de obalanserade implementeringarna, men inom telekom krävs det ofta att designen konverteras till den balanserade implementeringen när den används med balanserade linjer.	redigera

Modifierade stegtopologier

serie m-härledd topologi

Bildfilterdesign använder vanligtvis modifieringar av den grundläggande stegtopologin. Dessa topologier, uppfunna av Otto Zobel , har samma passband som stegen som de är baserade på, men deras överföringsfunktioner är modifierade för att förbättra vissa parametrar såsom impedansmatchning , stoppbandsförkastning eller passband-till-stoppband övergångsbranthet. Vanligtvis tillämpar designen en viss transformation på en enkel stegtopologi: den resulterande topologin är stegliknande men följer inte längre regeln att shuntadmittanser är det dubbla nätverket av serieimpedanser: den blir alltid mer komplex med högre komponentantal. Sådana topologier inkluderar;

Filtret av m-typ (m-derived) är den överlägset mest använda modifierade bildstegetopologin. Det finns två m-typ topologier för var och en av de grundläggande stegtopologierna; de seriehärledda och shunthärledda topologierna. Dessa har identiska överföringsfunktioner till varandra men olika bildimpedanser. Där ett filter designas med mer än ett passband, kommer m-typ topologin att resultera i ett filter där varje passband har ett analogt frekvensdomänsvar. Det är möjligt att generalisera m-typ-topologin för filter med mer än ett passband med hjälp av parametrar m 1 , _m 2 _, m ₃ etc., som inte är lika med varandra vilket resulterar i generella m _n -typ-filter som har bandformer som kan skiljer sig åt i olika delar av frekvensspektrumet.

Topologin av mm'-typ kan ses som en design av dubbel m-typ. Liksom m-typen har den samma bandform men erbjuder ytterligare förbättrade överföringsegenskaper. Det är dock en sällan använd design på grund av ökat komponentantal och komplexitet samt att det normalt kräver grundläggande stege- och m-typsektioner i samma filter för impedansanpassningsskäl. Det finns normalt bara i ett kompositfilter .

Bridged-T topologier

Typisk bryggad-T Zobel nätverksutjämnare som används för att korrigera high end roll-off

Zobels konstantresistansfilter använder en topologi som skiljer sig något från andra filtertyper, kännetecknas av att de har en konstant ingångsresistans vid alla frekvenser och genom att de använder resistiva komponenter i designen av sina sektioner. Det högre antalet komponenter och sektioner i dessa konstruktioner begränsar vanligtvis deras användning till utjämningsapplikationer. Topologier som vanligtvis förknippas med filter med konstant resistans är bryggt-T och dess varianter, alla beskrivna i Zobel-nätverkets artikel;

Bridged-T topologi
Balanserad bryggad-T-topologi
L-sektionstopologi med öppen krets
Kortslutning L-sektionstopologi
Balanserad C-sektionstopologi med öppen krets
Balanserad kortslutning C-sektionstopologi

Den överbryggade T-topologin används också i sektioner som är avsedda att producera en signalfördröjning men i detta fall används inga resistiva komponenter i konstruktionen.

Gittertopologi

Gittertopologi X-sektions faskorrigeringsfilter

Både T-sektionen (från stegtopologi) och brygg-T (från Zobel-topologi) kan omvandlas till en gittertopologifiltersektion, men i båda fallen resulterar detta i högt komponentantal och komplexitet. Den vanligaste tillämpningen av gitterfilter (X-sektioner) är i allpassfilter som används för fasutjämning .

Även om T- och bryggkopplade-T-sektioner alltid kan omvandlas till X-sektioner, är det omvända inte alltid möjligt på grund av möjligheten att negativa värden på induktans och kapacitans uppstår i transformationen.

Gittertopologin är identisk med den mer välbekanta brotopologin , skillnaden är bara den ritade representationen på sidan snarare än någon verklig skillnad i topologi, kretsar eller funktion.

Aktiva topologier

Multipel feedback topologi

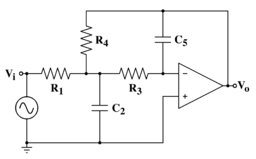
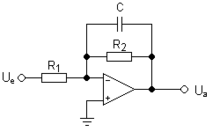
Multipel återkopplingstopologikrets.

Multipel återkopplingstopologi är en elektronisk filtertopologi som används för att implementera ett elektroniskt filter genom att lägga till två poler till överföringsfunktionen . Ett diagram över kretstopologin för ett andra ordningens lågpassfilter visas i figuren till höger.

Överföringsfunktionen för multipelåterkopplingstopologikretsen, som alla andra ordningens linjära filter , är:

H(s)={\frac {V_{o}} {V_{i}}}=-{\frac {1}{As^{2}+Bs+C}}={\frac {K{\omega _{0}}^{2}}{s^{ 2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}

.

I ett MF-filter,

A=(R_{1}R_{3}C_{2}C_{5})\,

B=R_{3}C_{5}+R_{1}C_{5}+R_{1}R_{3}C_{5}/R_{4}\ ,

C=R_{1}/R_{4}\,

Q={\frac {\sqrt {R_{3}R_{4}C_{2}C_{5}}}{(R_{4}+R_{3}+|K|R_{3} )C_{5}}}

är Q-faktorn .

K=-R_{4}/R_{1}\,

är DC-spänningsförstärkningen ω

\displaystyle \omega _{0}=2\pi f_{0}=1/{\sqrt {R_{3}R_{4}C_{2}C_{5}}}}

är hörnfrekvensen

För att hitta lämpliga komponentvärden för att uppnå önskade filteregenskaper kan ett liknande tillvägagångssätt användas som i avsnittet Designval i den alternativa Sallen–Key-topologin.

Biquad filter topologi

För den digitala implementeringen av ett biquad-filter, se Digitalt biquad-filter .

Ett biquad-filter är en typ av linjärt filter som implementerar en överföringsfunktion som är förhållandet mellan två kvadratiska funktioner . Namnet biquad är en förkortning för biquadratic . Alla andra ordningens filtertopologi kan hänvisas till som en biquad , till exempel MFB eller Sallen-Key. Det finns emellertid också en specifik "biquad"-topologi. Det kallas också ibland "ring av 3"-kretsen. ^{[ citat behövs ]}

Biquad-filter är vanligtvis aktiva och implementerade med en enkelförstärkare biquad (SAB) eller två-integrator-loop- topologi.

SAB - topologin använder återkoppling för att generera komplexa poler och möjligen komplexa nollor . I synnerhet flyttar återkopplingen de verkliga polerna i en RC-krets för att generera de rätta filteregenskaperna.
Två-integrator-loop-topologin härleds från att omarrangera en biquadratisk överföringsfunktion. Omarrangemanget kommer att likställa en signal med summan av en annan signal, dess integral och integralens integral. Med andra ord avslöjar omarrangemanget en tillståndsvariabel filterstruktur . Genom att använda olika tillstånd som utgångar kan alla typer av andra ordningens filter implementeras.

SAB-topologin är känslig för komponentval och kan vara svårare att justera. Därför hänvisar termen biquad vanligtvis till två-integrator-loop tillståndsvariabel filtertopologi.

Tow-Thomas filter

Figur 1. Den vanliga Tow-Thomas biquad-filtertopologin.

Till exempel kan grundkonfigurationen i figur 1 användas som antingen ett lågpass- eller bandpassfilter beroende på varifrån utsignalen tas.

Den andra ordningens lågpassöverföringsfunktion ges av

H(s)={\frac {G_{\mathrm {lpf} }{\omega _{0}}^{ 2}}{s^{2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}

där lågpassförstärkning $G_{\mathrm {lpf} }=-R_{2}/R_{1}$ . Andra ordningens bandpassöverföringsfunktion ges av

H(s)={\frac {G_{\mathrm {bpf} }{\frac {\omega _{0 }}{Q}}s}{s^{2}+{\frac {\omega _{0}}{Q}}s+{\omega _{0}}^{2}}}

.

med bandpassförstärkning $G_{\mathrm {bpf} }=-R_{3}/R_{1}$ . I båda fallen

Naturlig frekvens är $\omega _{0}=1/{\sqrt {R_{2}R_{4}C_{1}C_{2}}}$ .
Kvalitetsfaktorn är $Q={\sqrt {\frac {{R_{3}}^{2}C_{1}}{R_{2}R_{ 4}C_{2}}}}$ .

Bandbredden uppskattas av ${\displaystyle B=\omega _{0}/Q} , och$ ${\displaystyle \zeta =1/2Q$ uttrycks ibland som en dämpningskonstant . Om ett icke-inverterande lågpassfilter krävs, kan utgången tas vid utgången av den andra operationsförstärkaren , efter att den andra integratorns och växelriktarens ordning har kopplats om. Om ett icke-inverterande bandpassfilter krävs, kan ordningen för den andra integratorn och växelriktaren växlas och utgången tas vid utgången av växelriktarens operationsförstärkare.

Akerberg-Mossberg filter

Figur 2. Akerberg-Mossbergs biquad filtertopologi.

Figur 2 visar en variant av Tow-Thomas-topologin, känd som Akerberg-Mossberg-topologin, som använder en aktivt kompenserad Miller-integrator, vilket förbättrar filterprestanda.

Sallen–Key topologi

Figur 1: Den generiska Sallen-Key-filtertopologin

Sallen-Key-designen är ett icke-inverterande andra ordningens filter med möjlighet till hög Q och passbandsförstärkning.

Se även

Anteckningar

Campbell, GA, "Physical Theory of the Electric Wave-Filter", Bell System Technical Journal , november 1922, vol. 1, nr. 2, s. 1–32.
Zobel, OJ, "Theory and Design of Uniform and Composite Electric Wave Filters", Bell System Technical Journal , Vol. 2 (1923).
Foster, RM, "A reactance theorem", Bell System Technical Journal , Vol. 3 , s. 259–267, 1924.
Cauer, W, "Die Verwirklichung der Wechselstromwiderstande vorgeschriebener Frequenzabhängigkeit", Archiv für Elektrotechnik , 17 , s. 355–388, 1926.
Zobel, OJ, "Distortion correction in electrical networks with constant resistance recurrent networks", Bell System Technical Journal , Vol. 7 (1928), sid. 438.
Zobel, OJ, Phase-shifting network , US patent 1 792 523, inlämnat 12 mars 1927, utfärdat 17 februari 1931.

externa länkar

Media relaterade till elektronisk filtertopologi på Wikimedia Commons