
Linjens orientering vinkelrätt mot mittplanet av en tjock
pocketbok under böjning.
Timoshenko -Ehrenfest strålteorin utvecklades av Stephen Timoshenko och Paul Ehrenfest tidigt på 1900-talet. Modellen tar hänsyn till skjuvdeformation och rotationsböjningseffekter , vilket gör den lämplig för att beskriva beteendet hos tjocka strålar, sandwich-kompositstrålar eller strålar som utsätts för högfrekvent excitation när våglängden närmar sig strålens tjocklek. Den resulterande ekvationen är av 4:e ordningen, men till skillnad från Euler-Bernoullis strålteori finns det också en partiell derivata av andra ordningen. Fysiskt sänker man genom att ta hänsyn till de tillagda deformationsmekanismerna effektivt balkens styvhet, medan resultatet är en större avböjning under en statisk belastning och lägre förutsagda egenfrekvenser för en given uppsättning randvillkor. Den senare effekten är mer märkbar för högre frekvenser då våglängden blir kortare (i princip jämförbar med strålens höjd eller kortare), och därmed minskar avståndet mellan motstående skjuvkrafter.
Roterande tröghetseffekt introducerades av Bresse och Rayleigh.
Om strålmaterialets skjuvmodul närmar sig oändligheten – och därmed blir strålen stel i skjuvningen – och om rotationströghetseffekter försummas, konvergerar Timosjenkos strålteori mot vanlig strålteori .
Kvasistatisk Timosjenko-stråle

Deformation av en Timosjenko-stråle (blå) jämfört med den hos en Euler-Bernoulli-stråle (röd).

Deformation av en Timosjenko-stråle. Normalen roterar med ett belopp

som inte är lika med

.
I statisk Timosjenko strålteori utan axiella effekter antas strålens förskjutningar vara givna av

där  är koordinaterna för en punkt i strålen,
är koordinaterna för en punkt i strålen,  är komponenterna i förskjutningsvektorn i de tre koordinatriktningarna,
är komponenterna i förskjutningsvektorn i de tre koordinatriktningarna,  är rotationsvinkeln för normalen till strålens mittyta, och
är rotationsvinkeln för normalen till strålens mittyta, och  är förskjutningen av mellanytan i
är förskjutningen av mellanytan i  -riktningen.
-riktningen.
De styrande ekvationerna är följande kopplade system av vanliga differentialekvationer :

Timosjenkos strålteorin för det statiska fallet är ekvivalent med Euler-Bernoulli-teorin när den sista termen ovan försummas, en approximation som är giltig när

var
-
 är längden på strålen.
är längden på strålen.
-
 är tvärsnittsarean.
är tvärsnittsarean.
-
 är elasticitetsmodulen .
är elasticitetsmodulen .
-
 är skjuvmodulen .
är skjuvmodulen .
-
 är det andra ögonblicket av area .
är det andra ögonblicket av area .
-
 , kallad Timosjenko skjuvkoefficient, beror på geometrin. Normalt är
, kallad Timosjenko skjuvkoefficient, beror på geometrin. Normalt är  för en rektangulär sektion.
för en rektangulär sektion.
-
 är en fördelad last (kraft per längd).
är en fördelad last (kraft per längd).
Att kombinera de två ekvationerna ger, för en homogen stråle med konstant tvärsnitt,

Böjmomentet  och skjuvkraften
och skjuvkraften  i balken är relaterade till förskjutningen
i balken är relaterade till förskjutningen  och rotationen
och rotationen  . Dessa relationer, för en linjär elastisk Timosjenko-stråle, är:
. Dessa relationer, för en linjär elastisk Timosjenko-stråle, är:

| Härledning av kvasistatiska Timosjenko-stråleekvationer |
Från de kinematiska antagandena för en Timosjenko-stråle ges strålens förskjutningar av 
Sedan, från töjnings-förskjutningsrelationerna för små stammar, är stammarna som inte är noll baserade på Timosjenko-antagandena.

Eftersom den faktiska skjuvtöjningen i balken inte är konstant över tvärsnittet introducerar vi en korrektionsfaktor  så att så att

Variationen i strålens inre energi är
![{\displaystyle \delta U=\int _{L}\int _{A}(\sigma _{xx}\delta \varepsilon _{xx}+2\sigma _{xz}\delta \varepsilon _{xz})~\mathrm {d} A~\mathrm {d} L=\int _{L}\int _{A}\left[-z~\sigma _{xx}{\frac {\partial (\delta \varphi )}{\partial x}}+\sigma _{xz}~\kappa \left(-\delta \varphi +{\frac {\partial (\delta w)}{\partial x}}\right)\right]~\mathrm {d} A~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8538120f720cdf9758cf966457cc594ab501443)
Definiera

Sedan
![{\displaystyle \delta U=\int _{L}\left[-M_{xx}{\frac {\partial (\delta \varphi )}{\partial x}}+Q_{x}\left(-\delta \varphi +{\frac {\partial (\delta w)}{\partial x}}\right)\right]~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c36737b1d63a52a76cf0d34f07d97b340ccd61cb)
Integrering av delar, och att notera att på grund av randvillkoren variationerna är noll vid ändarna av strålen, leder till
![{\displaystyle \delta U=\int _{L}\left[\left({\frac {\partial M_{xx}}{\partial x}}-Q_{x}\right)~\delta \varphi -{\frac {\partial Q_{x}}{\partial x}}~\delta w\right]~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f25d6c444400ea89df8677e062734fb86236ac)
Variationen i det yttre arbetet som utförs på balken med en tvärlast  per längdenhet är per längdenhet är

Sedan, för en kvasistatisk stråle, ger principen om virtuellt arbete
![\delta U = \delta W \implies
\int_L \left[\left(\frac{\partial M_{xx}}{\partial x} - Q_x\right)~\delta\varphi - \left(\frac{\partial Q_{x}}{\partial x} + q\right)~\delta w\right]~\mathrm{d}L = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/d70338b0e41cd72e9b72cfa2dba0e4e4329467ee)
De styrande ekvationerna för strålen är, från variationskalkylens grundsats,

För en linjär elastisk balk

Därför kan de styrande ekvationerna för strålen uttryckas som
![\begin{align}
\frac{\partial }{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right) + \kappa AG~\left(\frac{\partial w}{\partial x}-\varphi\right) & = 0 \\
\frac{\partial }{\partial x}\left[\kappa AG\left(\frac{\partial w}{\partial x} - \varphi\right)\right] + q & = 0
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a1694f92bbda646acb7cbfca5f0497ff4165cac)
Att kombinera de två ekvationerna tillsammans ger

|
Gränsförhållanden
De två ekvationerna som beskriver deformationen av en Timosjenko-stråle måste utökas med randvillkor om de ska lösas. Fyra randvillkor krävs för att problemet ska vara väl ställt . Typiska randvillkor är:
-
Enkelt stödda balkar : Förskjutningen
 är noll vid placeringen av de två stöden. Böjmomentet
är noll vid placeringen av de två stöden. Böjmomentet  { som appliceras på balken måste också specificeras. Rotationen
{ som appliceras på balken måste också specificeras. Rotationen  och den tvärgående skjuvkraften
och den tvärgående skjuvkraften  är inte specificerade.
är inte specificerade.
-
Fastklämda balkar : Förskjutningen
 och rotationen
och rotationen  specificeras till noll i den fastklämda änden. Om en ände är fri måste skjuvkraft
specificeras till noll i den fastklämda änden. Om en ände är fri måste skjuvkraft  och böjmoment
och böjmoment  specificeras i den änden.
specificeras i den änden.
Spänn energi från en Timosjenko-stråle
Töjningsenergin för en Timosjenko-stråle uttrycks som summan av töjningsenergin på grund av böjning och skjuvning. Båda dessa komponenter är kvadratiska i sina variabler. Töjningsenergifunktionen för en Timosjenko-stråle kan skrivas som,
![{\displaystyle W=\int _{[0,L]}{\frac {EI}{2}}\left({\frac {d\varphi }{dx}}\right)^{2}+{\frac {kGA}{2}}\left(\varphi -{\frac {dw}{dx}}\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8752aec3d718d6531ccab7073983884dbfa8cb1f)
Exempel: Cantilever balk

En fribärande Timosjenko-balk under punktbelastning i den fria änden
För en fribärande balk är en gräns fastspänd medan den andra är fri. Låt oss använda ett högerhänt koordinatsystem där  -riktningen är positiv mot höger och
-riktningen är positiv mot höger och  -riktningen är positiv uppåt. Enligt normal konvention antar vi att positiva krafter verkar i positiva riktningar för
-riktningen är positiv uppåt. Enligt normal konvention antar vi att positiva krafter verkar i positiva riktningar för  och
och  -axlarna och positiva moment verkar i medurs riktning. Vi antar också att teckenkonventionen för spänningsresultanterna ( M
-axlarna och positiva moment verkar i medurs riktning. Vi antar också att teckenkonventionen för spänningsresultanterna ( M  och
och  ) är sådan att positiva böjmoment komprimerar materialet i botten av balken (lägre
) är sådan att positiva böjmoment komprimerar materialet i botten av balken (lägre  -koordinater) och positiva skjuvkrafter roterar strålen moturs.
-koordinater) och positiva skjuvkrafter roterar strålen moturs.
Låt oss anta att den fastklämda änden är vid  och den fria änden är vid
och den fria änden är vid  . Om en punktbelastning
. Om en punktbelastning  appliceras på den fria änden i den positiva
appliceras på den fria änden i den positiva  -riktningen, ger ett frikroppsdiagram av strålen oss
-riktningen, ger ett frikroppsdiagram av strålen oss

och

Därför har vi från uttrycken för böjmomentet och skjuvkraften

Integration av den första ekvationen, och tillämpning av gränsvillkoret  vid
vid  , leder till
, leder till

Den andra ekvationen kan sedan skrivas som

Integration och tillämpning av gränsvillkoret  vid
vid  ger
ger

Den axiella spänningen ges av

Dynamisk Timosjenko-stråle
I Timosjenko strålteori utan axiella effekter antas strålens förskjutningar vara givna av

där  är koordinaterna för en punkt i strålen,
är koordinaterna för en punkt i strålen,  är komponenterna i förskjutningsvektorn i de tre koordinatriktningarna,
är komponenterna i förskjutningsvektorn i de tre koordinatriktningarna,  är rotationsvinkeln för normalen till strålens mittyta, och
är rotationsvinkeln för normalen till strålens mittyta, och  är förskjutningen av mellanytan i
är förskjutningen av mellanytan i  -riktningen.
-riktningen.
Med utgångspunkt från ovanstående antagande kan Timosjenkos strålteorin, som tillåter vibrationer, beskrivas med de kopplade linjära partiella differentialekvationerna :
![\rho A\frac{\partial^{2}w}{\partial t^{2}} - q(x,t) = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ae3e2d14c1b5e59f0e4cd53c7a506b7d1111f8)

där de beroende variablerna är  , strålens translationella förskjutning och
, strålens translationella förskjutning och  , vinkeln förflyttning. Observera att till skillnad från Euler-Bernoulli- teorin är vinkelavböjningen en annan variabel och inte approximeras av lutningen på avböjningen. Också,
, vinkeln förflyttning. Observera att till skillnad från Euler-Bernoulli- teorin är vinkelavböjningen en annan variabel och inte approximeras av lutningen på avböjningen. Också,
-
 är densiteten för strålmaterialet (men inte den linjära densiteten ) .
är densiteten för strålmaterialet (men inte den linjära densiteten ) .
-
 är tvärsnittsarean.
är tvärsnittsarean.
-
 är elasticitetsmodulen .
är elasticitetsmodulen .
-
 är skjuvmodulen .
är skjuvmodulen .
-
 är det andra ögonblicket av area .
är det andra ögonblicket av area .
-
 , kallad Timosjenko skjuvkoefficient, beror på geometrin. Normalt är
, kallad Timosjenko skjuvkoefficient, beror på geometrin. Normalt är  för en rektangulär sektion.
för en rektangulär sektion.
-
 är en fördelad last (kraft per längd).
är en fördelad last (kraft per längd).


Dessa parametrar är inte nödvändigtvis konstanter.
För en linjär elastisk, isotrop, homogen stråle med konstant tvärsnitt kan dessa två ekvationer kombineras för att ge

| Härledning av kombinerad Timosjenkos strålekvation |
Ekvationerna som styr böjningen av en homogen Timosjenko-stråle med konstant tvärsnitt är 
Från ekvation (1), med antagande av lämplig jämnhet, har vi

Differentieringsekvation (2) ger

Genom att ersätta ekvation (3), (4), (5) med ekvation (6) och omordna, får vi

|
Timosjenko-ekvationen förutsäger en kritisk frekvens  . Eftersom det är en fjärde ordningens ekvation finns det fyra oberoende lösningar, två oscillerande och två evanescenta för frekvenser under
. Eftersom det är en fjärde ordningens ekvation finns det fyra oberoende lösningar, två oscillerande och två evanescenta för frekvenser under  . För frekvenser större än
. För frekvenser större än  är alla lösningar oscillerande och som en konsekvens uppstår ett andra spektrum.
är alla lösningar oscillerande och som en konsekvens uppstår ett andra spektrum.
Axiella effekter
Om strålens förskjutningar ges av

där  är en ytterligare förskjutning i
är en ytterligare förskjutning i  -riktningen, då tar de styrande ekvationerna för en Timosjenko-stråle formen
-riktningen, då tar de styrande ekvationerna för en Timosjenko-stråle formen
![\begin{align}
m \frac{\partial^{2}w}{\partial t^{2}} & = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] + q(x,t) \\
J \frac{\partial^{2}\varphi}{\partial t^{2}} & = N(x,t)~\frac{\partial w}{\partial x} + \frac{\partial}{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right)+\kappa AG\left(\frac{\partial w}{\partial x}-\varphi\right)
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c35d8e346f27ef78d0a9c29ac3449ed4fb94b21)
där  och
och  är en externt applicerad axiell kraft. Varje yttre axiell kraft balanseras av spänningsresultanten
är en externt applicerad axiell kraft. Varje yttre axiell kraft balanseras av spänningsresultanten

där  är den axiella spänningen och tjockleken på strålen har antagits vara
är den axiella spänningen och tjockleken på strålen har antagits vara  .
.
Den kombinerade strålekvationen med axialkraftseffekter ingår är

Dämpning
Om vi förutom axiella krafter antar en dämpningskraft som är proportionell mot hastigheten med formen

de kopplade styrande ekvationerna för en Timosjenko-stråle tar formen
![m \frac{\partial^{2}w}{\partial t^{2}} + \eta(x)~\cfrac{\partial w}{\partial t} = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] + q(x,t)](https://wikimedia.org/api/rest_v1/media/math/render/svg/f72225eea89af02d344a6877126ab80e276b33c9)

och den kombinerade ekvationen blir

En varning för denna Ansatz-dämpningskraft (som liknar viskositet) är att medan viskositet leder till en frekvensberoende och amplitudoberoende dämpningshastighet för strålsvängningar, är de empiriskt uppmätta dämpningshastigheterna frekvensokänsliga, men beror på amplituden av strålavböjningen .
Skjuvningskoefficient
Att bestämma skjuvkoefficienten är inte okomplicerat (inte heller är de bestämda värdena allmänt accepterade, dvs. det finns mer än ett svar); i allmänhet måste den uppfylla:
-
 .
.
Skjuvningskoefficienten beror på Poissons förhållande . Försöken att ge exakta uttryck gjordes av många forskare, inklusive Stephen Timoshenko , Raymond D. Mindlin , GR Cowper, NG Stephen, JR Hutchinson etc. (se även härledningen av Timosjenkos strålteorin som en förfinad strålteori baserad på variationen -asymptotisk metod i boken av Khanh C. Le som leder till olika skjuvningskoefficienter i statiska och dynamiska fall). I ingenjörspraktik är uttrycken av Stephen Timosjenko tillräckliga i de flesta fall. 1975 publicerade Kaneko en utmärkt genomgång av studier av skjuvkoefficienten. På senare tid visar nya experimentella data att skjuvningskoefficienten är underskattad.
Korrigerande skjuvningskoefficienter för homogen isotrop stråle enligt Cowper - val.
| Tvärsnitt |
Koefficient |

|

|

|

|

|

|

|

|

|
 , där , där 
|

|

|

|

|

|
 där där  och och 
|
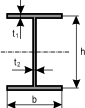
|
 , där , där  och och 
|
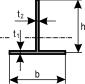
|
 där där  och och 
|
där  är Poissons förhållande.
är Poissons förhållande.
Se även





































![{\displaystyle \delta U=\int _{L}\int _{A}(\sigma _{xx}\delta \varepsilon _{xx}+2\sigma _{xz}\delta \varepsilon _{xz})~\mathrm {d} A~\mathrm {d} L=\int _{L}\int _{A}\left[-z~\sigma _{xx}{\frac {\partial (\delta \varphi )}{\partial x}}+\sigma _{xz}~\kappa \left(-\delta \varphi +{\frac {\partial (\delta w)}{\partial x}}\right)\right]~\mathrm {d} A~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c8538120f720cdf9758cf966457cc594ab501443)

![{\displaystyle \delta U=\int _{L}\left[-M_{xx}{\frac {\partial (\delta \varphi )}{\partial x}}+Q_{x}\left(-\delta \varphi +{\frac {\partial (\delta w)}{\partial x}}\right)\right]~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c36737b1d63a52a76cf0d34f07d97b340ccd61cb)
![{\displaystyle \delta U=\int _{L}\left[\left({\frac {\partial M_{xx}}{\partial x}}-Q_{x}\right)~\delta \varphi -{\frac {\partial Q_{x}}{\partial x}}~\delta w\right]~\mathrm {d} L}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34f25d6c444400ea89df8677e062734fb86236ac)


![\delta U = \delta W \implies
\int_L \left[\left(\frac{\partial M_{xx}}{\partial x} - Q_x\right)~\delta\varphi - \left(\frac{\partial Q_{x}}{\partial x} + q\right)~\delta w\right]~\mathrm{d}L = 0](https://wikimedia.org/api/rest_v1/media/math/render/svg/d70338b0e41cd72e9b72cfa2dba0e4e4329467ee)


![\begin{align}
\frac{\partial }{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right) + \kappa AG~\left(\frac{\partial w}{\partial x}-\varphi\right) & = 0 \\
\frac{\partial }{\partial x}\left[\kappa AG\left(\frac{\partial w}{\partial x} - \varphi\right)\right] + q & = 0
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a1694f92bbda646acb7cbfca5f0497ff4165cac)

![{\displaystyle W=\int _{[0,L]}{\frac {EI}{2}}\left({\frac {d\varphi }{dx}}\right)^{2}+{\frac {kGA}{2}}\left(\varphi -{\frac {dw}{dx}}\right)^{2}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8752aec3d718d6531ccab7073983884dbfa8cb1f)















![\rho A\frac{\partial^{2}w}{\partial t^{2}} - q(x,t) = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e5ae3e2d14c1b5e59f0e4cd53c7a506b7d1111f8)















![\begin{align}
m \frac{\partial^{2}w}{\partial t^{2}} & = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] + q(x,t) \\
J \frac{\partial^{2}\varphi}{\partial t^{2}} & = N(x,t)~\frac{\partial w}{\partial x} + \frac{\partial}{\partial x}\left(EI\frac{\partial \varphi}{\partial x}\right)+\kappa AG\left(\frac{\partial w}{\partial x}-\varphi\right)
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c35d8e346f27ef78d0a9c29ac3449ed4fb94b21)







![m \frac{\partial^{2}w}{\partial t^{2}} + \eta(x)~\cfrac{\partial w}{\partial t} = \frac{\partial}{\partial x}\left[ \kappa AG \left(\frac{\partial w}{\partial x}-\varphi\right)\right] + q(x,t)](https://wikimedia.org/api/rest_v1/media/math/render/svg/f72225eea89af02d344a6877126ab80e276b33c9)

















