Tabell med enkla kubikdiagram

De anslutna 3-regelbundna ( kubiska ) enkla graferna är listade för små vertexnummer.

Anslutningsmöjligheter

Antalet sammankopplade enkla kubiska grafer på 4, 6, 8, 10, ... hörn är 1, 2, 5, 19, ... (sekvens A002851 i OEIS ). En klassificering efter kantanslutningar görs enligt följande: 1-anslutna och 2-anslutna grafer definieras som vanligt. Detta lämnar de andra graferna i den 3-kopplade klassen eftersom varje 3-regelbunden graf kan delas genom att skära alla kanter intill någon av hörnen. För att förfina denna definition i ljuset av algebra för koppling av vinkelmoment (se nedan), är en underindelning av de 3-kopplade graferna till hjälp. Vi ska ringa

Icke-trivialt 3-kopplade de som kan delas av 3 kantskärningar till subgrafer med minst två hörn kvar i varje del
Cykliskt 4-anslutna – alla de som inte är 1-anslutna, inte 2-anslutna och inte icke-trivialt 3-anslutna

Detta deklarerar siffrorna 3 och 4 i den fjärde kolumnen i tabellerna nedan.

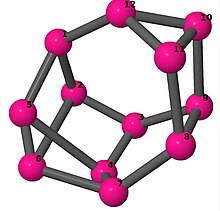
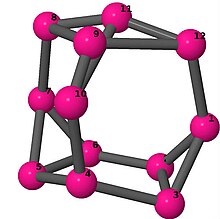
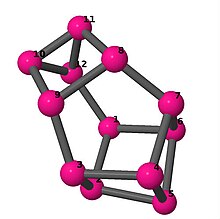
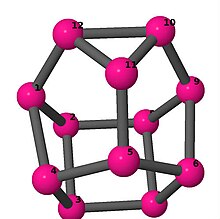
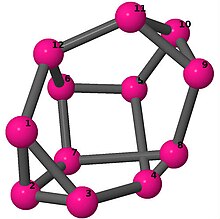
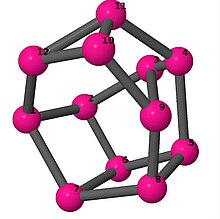
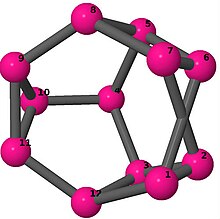
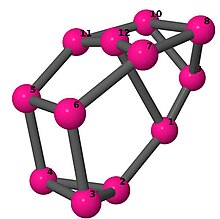
Bilder

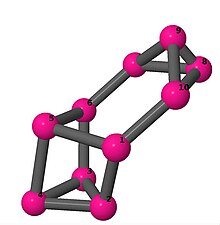
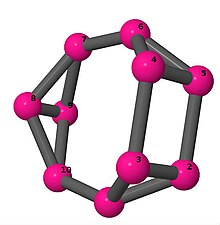
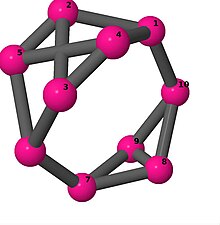
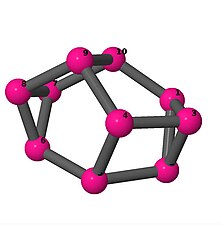
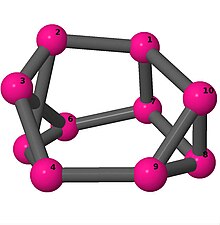
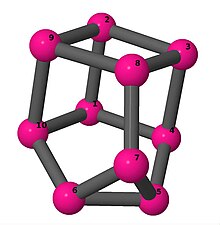
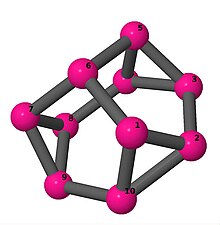
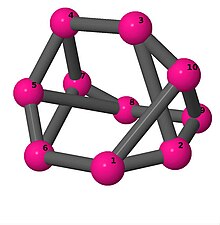
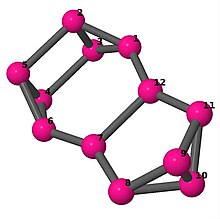
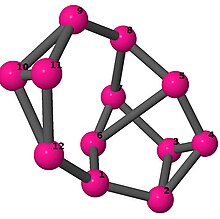
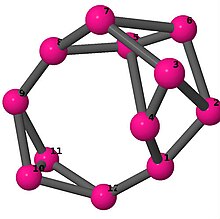
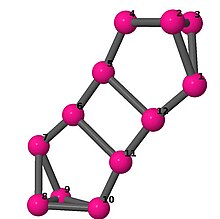
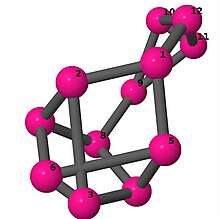
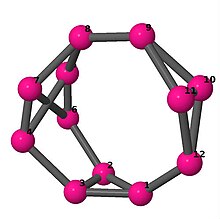
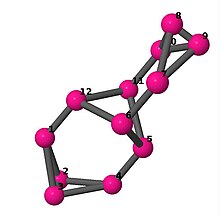
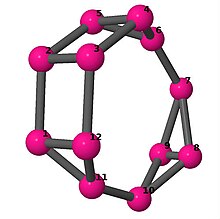
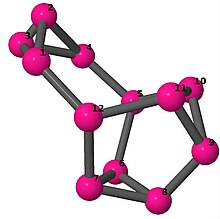
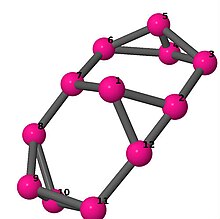
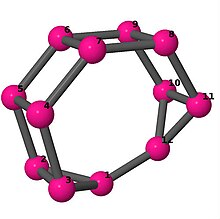
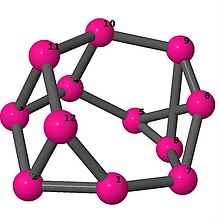
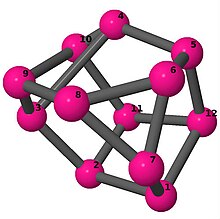
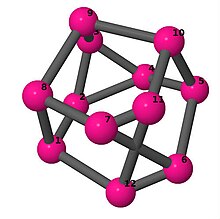
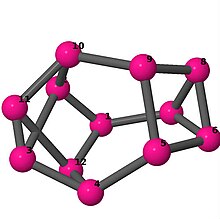
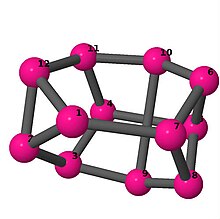
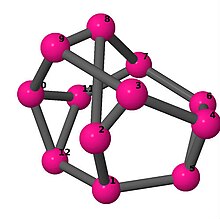
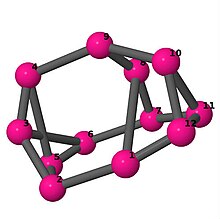
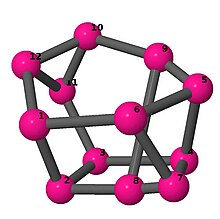
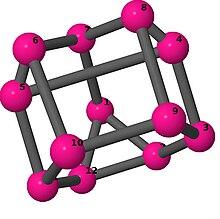
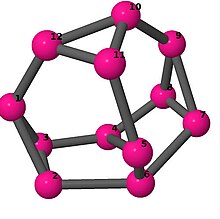
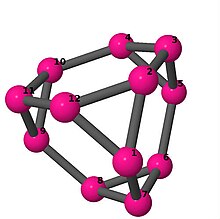
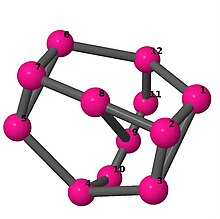
Ball-and-stick-modeller av graferna i en annan kolumn i tabellen visar hörn och kanter i stil med bilder av molekylära bindningar. Kommentarer till de enskilda bilderna innehåller omkrets , diameter , Wienerindex , Estradaindex och Kirchhoffindex . Aut är ordningen för automorfismgruppen i grafen. En Hamiltonsk krets (där den finns) indikeras genom att räkna upp hörn längs den banan från 1 och uppåt. (Positionerna för hörnen har definierats genom att minimera en parpotential definierad av den kvadratiska skillnaden mellan det euklidiska och grafteoretiska avståndet, placerat i en Molfile , sedan renderat med Jmol .)

LCF-notation

LCF -notationen är en notation av Joshua Lederberg , Coxeter och Frucht , för representation av kubiska grafer som är Hamiltonska .

De två kanterna längs cykeln som gränsar till någon av hörnen är inte nedskrivna.

Låt $v$ vara grafens hörn och beskriv den Hamiltonska cirkeln längs $p$ -hörnen med kantsekvensen $0 v v 1, v 1 v 2, ...,v p-2 v p-1, v p-1 v 0$ . När du stannar vid en vertex $v i$ , finns det en unik vertex $v j$ på ett avstånd $d i$ förenad av ett ackord med $v i$ ,

j=i+d_{i}\quad ({\bmod {\,}}p),\quad 2\leq d_{i}\leq p-2.

Vektorn $0 [d , d 1, ..., d p-1]$ för $p$ -heltalen är en lämplig men inte unik representation av den kubiska Hamiltonska grafen. Detta kompletteras med två ytterligare regler:

Om a $d i > p/2$ , ersätt det med $d i - p$ ;
undvik upprepning av en sekvens av $d i$ om dessa är periodiska och ersätt dem med en exponentiell notation.

Eftersom startpunkten för banan inte har någon betydelse, kan siffrorna i representationen vara cykliskt permuterade. Om en graf innehåller olika Hamiltonska kretsar kan man välja en av dessa för att passa notationen. Samma graf kan ha olika LCF-notationer, beroende på exakt hur hörnen är ordnade.

Ofta antipalindromiska representationer med

d_{p-1-i}=-d_{i}\quad ({\bmod { \,}}p),\quad i=0,1,\ldots p/2-1

är att föredra (om de finns), och den redundanta delen ersätts då av ett semikolon och ett bindestreck "; –". LCF-notationen $[5, -9, 7, -7, 9, -5] 4$ , till exempel, och skulle i det skedet kondenseras till $[5, -9, 7; -] 4$ .

Tabell

4 hörn

diam.	omkrets	Aut.	ansluta.	LCF	namn	bild
1	3	24	4	[2] ⁴	K ₄	4 hörn och 6 kanter. Yutsis-graf för 6-j-symbolen

6 hörn

diam.	omkrets	Aut.	ansluta.	LCF	namn	bild
2	3	12	3	[2, 3, −2] ²	prismagraf Y ₃	6 hörn och 9 kanter
2	4	72	4	[3] ⁶	K _{3, 3} , bruksdiagram	6 hörn och 9 kanter. Yutsis-graf för 9-j-symbolen .

8 hörn

diam.	omkrets	Aut.	ansluta.	LCF	namn	bilder
3	3	16	2	[2, 2, −2, −2] ²		8 hörn och 12 kanter
3	3	4	3	[4, −2, 4, 2] ² eller [2, 3, −2, 3; –]		8 hörn och 12 kanter
2	3	12	3	[2, 4, −2, 3, 3, 4, −3, −3]		8 hörn och 12 kanter
3	4	48	4	[−3, 3] ⁴	kubisk graf	8 hörn och 12 kanter. Yutsis-graf av 12j-symbolen av det andra slaget.
2	4	16	4	[4] ⁸ eller [4, −3, 3, 4] ²	Wagner graf	8 hörn och 12 kanter. Yutsis-graf av 12j-symbolen av det första slaget.

10 hörn

diam.	omkrets	Aut.	ansluta.	LCF	namn	bilder
5	3	32	1		Kantlista 0–1, 0–6, 0–9, 1–2, 1–5, 2–3, 2–4, 3–4, 3–5, 4–5, 6–7, 6–8, 7–8, 7–9, 8–9	10 hörn och 15 kanter
4	3	4	2	[4, 2, 3, −2, −4, −3, 2, 2, −2, −2]
3	3	8	2	[2, -3, -2, 2, 2; –]
3	3	16	2	[−2, −2, 3, 3, 3; –]
4	3	16	2	[2, 2, −2, −2, 5] ²
3	3	2	3	[2, 3, −2, 5, −3] ² [3, −2, 4, −3, 4, 2, −4, −2, −4, 2]
3	3	12	3	[2, −4, −2, 5, 2, 4, −2, 4, 5, −4]		10 hörn och 15 kanter
3	3	2	3	[5, 3, 5, −4, −3, 5, 2, 5, −2, 4] [ −4, 2, 5, −2, 4, 4, 4, 5, −4, −4] [ −3, 2, 4, −2, 4, 4, −4, 3, −4, −4]		10 hörn och 15 kanter
3	3	4	3	[−4, 3, 3, 5, −3, −3, 4, 2, 5, −2] [3, −4, −3, −3, 2, 3, −2, 4, −3, 3 ]
3	3	6	3	[3, −3, 5, −3, 2, 4, −2, 5, 3, −4]
3	3	4	3	[2, 3, −2, 3, −3; –] [−4, 4, 2, 5, −2] ²
3	3	6	3	[5, −2, 2, 4, −2, 5, 2, −4, −2, 2]
3	3	8	3	[2, 5, −2, 5, 5] ² [2, 4, −2, 3, 4; –]		10 hörn och 15 kanter
3	4	48	3	[5, −3, −3, 3, 3] ²
3	4	8	4	[5, −4, 4, −4, 4] ² [5, −4, −3, 3, 4, 5, −3, 4, −4, 3]		Yutsis-graf av 15j-symbolen av det tredje slaget.
3	4	4	4	[5, −4, 4, 5, 5] ² [−3, 4, −3, 3, 4; –] [4, −3, 4, 4, −4; –] [−4, 3, 5, 5, −3, 4, 4, 5, 5, −4]		Yutsis-graf av 15j-symbolen av det fjärde slaget.
3	4	20	4	[5] ¹⁰ [−3, 3] ⁵ [5, 5, −3, 5, 3] ²		Yutsis-graf av 15j-symbolen av det första slaget.
3	4	20	4	[−4, 4, −3, 5, 3] ²	G _{5, 2}	Yutsis-graf av 15j-symbolen av det andra slaget.
2	5	120	4		Petersen graf	Yutsis-graf av 15j-symbolen av det femte slaget.

12 hörn

diam.	omkrets	Aut.	ansluta.	LCF	namn	bild
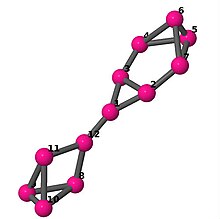
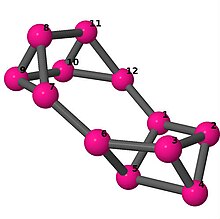
6	3	16	1		Kantlista 0–1, 0–2, 0–11, 1–2, 1–6, 2–3, 3–4, 3–5, 4–5, 4–6, 5–6, 7–8, 7–9, 7–11, 8–9, 8–10, 9–10, 10–11
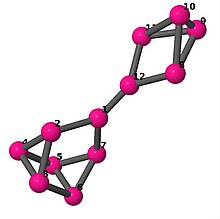
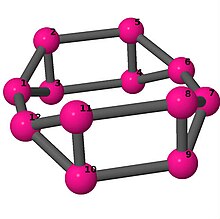
5	3	16	1		Kantlista 0–1, 0–6, 0–11, 1–2, 1–3, 2–3, 2–5, 3–4, 4–5, 4–6, 5–6, 7–8, 7–9, 7–11, 8–9, 8–10, 9–10, 10–11
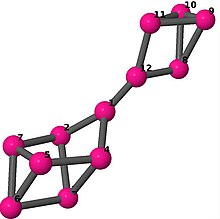
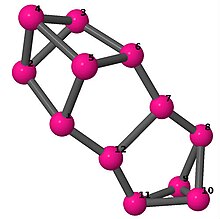
6	3	8	1		Kantlista 0–1, 0–3, 0–11, 1–2, 1–6, 2–3, 2–5, 3–4, 4–5, 4–6, 5–6, 7–8, 7–9, 7–11, 8–9, 8–10, 9–10, 10–11
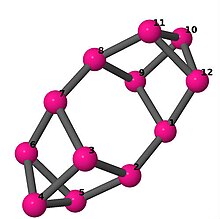
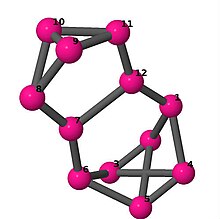
5	3	32	1		Kantlista 0–1, 0–6, 0–11, 1–2, 1–4, 2–3, 2–5, 3–4, 3–6, 4–5, 5–6, 7–8, 7–9, 7–11, 8–9, 8–10, 9–10, 10–11
5	3	4	2	[3, −2, −4, −3, 4, 2] ² [4, 2, 3, −2, −4, −3; –]
4	3	8	2	[3, −2, −4, −3, 3, 3, 3, −3, −3, −3, 4, 2]
4	3	4	2	[4, 2, 3, −2, −4, −3, 2, 3, −2, 2, −3, −2]
4	4	64	2	[3, 3, 3, −3, −3, −3] ²
4	3	16	2	[2, -3, -2, 3, 3, 3; –]
4	3	16	2	[2, 3, −2, 2, −3, −2] ²
4	3	2	2	[−2, 3, 6, 3, −3, 2, −3, −2, 6, 2, 2, −2] [4, 2, −4, −2, −4, 6, 2, 2, −2, −2, 4, 6]
4	3	8	2	[6, 3, 3, 4, −3, −3, 6, −4, 2, 2, −2, −2]
5	3	4	2	[4, 2, 3, −2, −4, −3, 5, 2, 2, −2, −2, −5]
4	3	16	2	[−3, −3, −3, 5, 2, 2; –]
4	3	8	2	[2, -3, -2, 5, 2, 2; –]
4	3	4	2	[2, 4, −2, 3, −5, −4, −3, 2, 2, −2, −2, 5] [5, 2, −4, −2, −5, −5, 2, 2, −2, −2, 4, 5]
4	3	4	2	[−2, -2, 4, 4, 4, 4; –] [3, −4, −4, −3, 2, 2; –] [5, 3, 4, 4, −3, −5, −4, −4, 2, 2, −2, −2]
4	3	2	2	[4, −2, 4, 2, −4, −2, −4, 2, 2, −2, −2, 2] [5, −2, 2, 3, −2 , −5, −3, 2, 2, −2, −2, 2]
5	3	16	2	[2, 2, −2, −2, −5, 5] ²
4	3	8	2	[−2, -2, 4, 5, 3, 4; –]
4	3	4	2	[5, 2, −3, −2, 6, −5, 2, 2, −2, −2, 6, 3]
4	3	8	2	[4, −2, 3, 3, −4, −3, −3, 2, 2, −2, −2, 2]
4	3	8	2	[−2, -2, 5, 3, 5, 3; –] [−2, −2, 3, 5, 3, −3; –]
5	3	32	2	[2, 2, −2, −2, 6, 6] ²
4	3	8	2	[−3, 2, −3, −2, 2, 2; –]
4	3	8	2	[−2, −2, 5, 2, 5, −2; –]
4	3	8	2	[6, −2, 2, 2, −2, −2, 6, 2, 2, −2, −2, 2]
4	3	48	2	[−2, −2, 2, 2] ³
4	3	4	3	[2, 3, −2, 3, −3, 3; –] [−4, 6, 4, 2, 6, −2] ²
4	3	4	3	[−4, 6, 3, 3, 6, −3, −3, 6, 4, 2, 6, −2] [−2, 3, −3, 4, −3, 3, 3, −4, −3, −3, 2, 3]
4	3	1	3	[−5, 2, −3, −2, 6, 4, 2, 5, −2, −4, 6, 3] [ −2, 3, −3, 4, −3, 4, 2, −4 , −2, −4, 2, 3] [3, −2, 3, −3, 5, −3, 2, 3, −2, −5, −3, 2]
3	3	4	3	[−5, −5, 4, 2, 6, −2, −4, 5, 5, 2, 6, −2] [4, −2, 3, 4, −4, −3, 3, −4 , 2, −3, −2, 2]
3	3	8	3	[−5, −5, 3, 3, 6, −3, −3, 5, 5, 2, 6, −2] [ 2, 4, −2, 3, 5, −4, −3, 3, 3, −5, −3, −3]
4	3	2	3	[2, 4, −2, 3, 6, −4, −3, 2, 3, −2, 6, −3] [ 2, 4, −2, 3, 5, −4, −3, 4, 2, −5, −2, −4] [−5, 2, −3, −2, 5, 5, 2, 5, −2, −5, −5, 3]
4	3	2	3	[−5, 2, −3, −2, 6, 3, 3, 5, −3, −3, 6, 3] [4, −2, −4, 4, −4, 3, 3, −4 , −3, −3, 4, 2] [−3, 3, 3, 4, −3, −3, 5, −4, 2, 3, −2, −5]
4	3	2	3	[2, 3, −2, 4, −3, 6, 3, −4, 2, −3, −2, 6] [−4, 5, −4, 2, 3, −2, −5, − 3, 4, 2, 4, −2]
4	3	1	3	[6, 3, −4, −4, −3, 3, 6, 2, −3, −2, 4, 4] [−5, −4, 4, 2, 6, −2, −4, 5 , 3, 4, 6, −3] [3, 4, 4, −3, 4, −4, −4, 3, −4, 2, −3, −2] [ 4, 5, −4, − 4, −4, 3, −5, 2, −3, −2, 4, 4] [4, 5, −3, −5, −4, 3, −5, 2, −3, −2, 5 , 3]
3	4	4	3	[4, 6, −4, −4, −4, 3, 3, 6, −3, −3, 4, 4] [−5, −4, 3, 3, 6, −3, −3, 5 , 3, 4, 6, −3] [4, −3, 5, −4, −4, 3, 3, −5, −3, −3, 3, 4]
3	4	16	3	[3, 3, 4, -3, -3, 4; –] [3, 6, −3, −3, 6, 3] ²
4	3	1	3	[4, −2, 5, 2, −4, −2, 3, −5, 2, −3, −2, 2] [5, −2, 2, 4, −2, −5, 3, − 4, 2, −3, −2, 2] [2, −5, −2, −4, 2, 5, −2, 2, 5, −2, −5, 4]	Frucht graf
4	3	4	3	[−2, 6, 2, −4, −2, 3, 3, 6, −3, −3, 2, 4] [ −2, 2, 5, −2, −5, 3, 3, −5 , −3, −3, 2, 5]
4	3	2	3	[2, 4, −2, 6, 2, −4, −2, 4, 2, 6, −2, −4] [ 2, 5, −2, 2, 6, −2, −5, 2, 3, −2, 6, −3]
4	3	2	3	[6, 3, −3, −5, −3, 3, 6, 2, −3, −2, 5, 3] [ 3, 5, 3, −3, 4, −3, −5, 3, −4, 2, −3, −2] [−5, −3, 4, 2, 5, −2, −4, 5, 3, −5, 3, −3]
4	4	12	3	[3, −3, 5, −3, −5, 3, 3, −5, −3, −3, 3, 5]
4	3	2	3	[4, 2, 4, -2, -4, 4; –] [3, 5, 2, −3, −2, 5; –] [6, 2, −3, −2, 6, 3] ²
4	3	2	3	[3, 6, 4, −3, 6, 3, −4, 6, −3, 2, 6, −2] [4, −4, 5, 3, −4, 6, −3, −5, 2, 4, −2, 6] [−5, 5, 3, −5, 4, −3, −5, 5, −4, 2, 5, −2]
3	3	1	3	[6, −5, 2, 6, −2, 6, 6, 3, 5, 6, −3, 6] [6, 2, −5, −2, 4, 6, 6, 3, −4, 5, −3, 6] [5, 5, 6, 4, 6, −5, −5, −4, 6, 2, 6, −2] [ −4, 4, −3, 3, 6, − 4, −3, 2, 4, −2, 6, 3] [6, 2, −4, −2, 4, 4, 6, 4, −4, −4, 4, −4] [ −3, 2, 5, −2, −5, 3, 4, −5, −3, 3, −4, 5] [ −5, 2, −4, −2, 4, 4, 5, 5, −4, −4, 4, −5]
3	3	2	3	[2, 6, −2, 5, 6, 4, 5, 6, −5, −4, 6, −5] [5, 6, −4, −4, 5, −5, 2, 6, − 2, −5, 4, 4] [2, 4, −2, −5, 4, −4, 3, 4, −4, −3, 5, −4] [ 2, −5, −2, 4 , −5, 4, 4, −4, 5, −4, −4, 5]
4	3	4	3	[2, 4, −2, −5, 5] ² [−5, 2, 4, −2, 6, 3, −4, 5, −3, 2, 6, −2]
4	3	2	3	[−4, −4, 4, 2, 6, −2, −4, 4, 4, 4, 6, −4] [ −4, −3, 4, 2, 5, −2, −4, 4 , 4, −5, 3, −4] [−3, 5, 3, 4, −5, −3, −5, −4, 2, 3, −2, 5]
3	3	2	3	[2, 5, -2, 4, 4, 5; –] [2, 4, −2, 4, 4, −4; –] [−5, 5, 6, 2, 6, −2] ² [5, −2, 4, 6, 3, −5, −4, −3, 2, 6, −2, 2]
3	3	2	3	[3, 6, −4, −3, 5, 6, 2, 6, −2, −5, 4, 6] [2, −5, −2, 4, 5, 6, 4, −4, 5 , −5, −4, 6] [5, −4, 4, −4, 3, −5, −4, −3, 2, 4, −2, 4]
4	3	2	3	[6, −5, 2, 4, −2, 5, 6, −4, 5, 2, −5, −2] [−2, 4, 5, 6, −5, −4, 2, −5 , −2, 6, 2, 5] [5, −2, 4, −5, 4, −5, −4, 2, −4, −2, 5, 2]
4	3	1	3	[2, −5, −2, 6, 3, 6, 4, −3, 5, 6, −4, 6] [6, 3, −3, 4, −3, 4, 6, −4, 2 , −4, −2, 3] [5, −4, 6, −4, 2, −5, −2, 3, 6, 4, −3, 4] [ 5, −3, 5, 6, 2 , −5, −2, −5, 3, 6, 3, −3] [−5, 2, −5, −2, 6, 3, 5, 5, −3, 5, 6, −5] [ −3, 4, 5, −5, −5, −4, 2, −5, −2, 3, 5, 5] [ 5, 5, 5, −5, 4, −5, −5, −5 , −4, 2, 5, −2]
3	3	2	3	[5, −3, 6, 3, −5, −5, −3, 2, 6, −2, 3, 5] [ 2, 6, −2, −5, 5, 3, 5, 6, − 3, −5, 5, −5] [5, 5, 5, 6, −5, −5, −5, −5, 2, 6, −2, 5] [4, −3, 5, 2, −4, −2, 3, −5, 3, −3, 3, −3] [5, 5, −3, −5, 4, −5, −5, 2, −4, −2, 5, 3]
4	3	4	3	[2, 4, -2, 5, 3, -4; –] [5, −3, 2, 5, −2, −5; –] [3, 6, 3, −3, 6, −3, 2, 6, −2, 2, 6, −2]
4	3	2	3	[6, 2, −4, −2, −5, 3, 6, 2, −3, −2, 4, 5] [ 2, 3, −2, 4, −3, 4, 5, −4, 2, −4, −2, −5] [−5, 2, −4, −2, −5, 4, 2, 5, −2, −4, 4, 5]
3	3	2	3	[5, 2, 5, -2, 5, -5; –] [6, 2, −4, −2, 4, 6] ² [2, −5, −2, 6, 2, 6, −2, 3, 5, 6, −3, 6] [ −5 , −2, 6, 6, 2, 5, −2, 5, 6, 6, −5, 2]
3	3	12	3	[−5, 3, 3, 5, −3, −3, 4, 5, −5, 2, −4, −2]
3	3	2	3	[6, −4, 3, 4, −5, −3, 6, −4, 2, 4, −2, 5] [−4, 6, −4, 2, 5, −2, 5, 6, 4, −5, 4, −5] [5, −5, 4, −5, 3, −5, −4, −3, 5, 2, 5, −2]
4	3	12	3	[−4, 5, 2, −4, −2, 5; –]	Dürer graf
3	3	4	3	[2, 5, -2, 5, 3, 5; –] [6, −2, 6, 6, 6, 2] ² [5, −2, 6, 6, 2, −5, −2, 3, 6, 6, −3, 2]
3	3	4	3	[6, −2, 6, 4, 6, 4, 6, −4, 6, −4, 6, 2] [5, 6, −3, 3, 5, −5, −3, 6, 2, −5, −2, 3]
3	3	4	3	[4, −2, 4, 6, −4, 2, −4, −2, 2, 6, −2, 2] [5, −2, 5, 6, 2, −5, −2, −5 , 2, 6, −2, 2]
3	3	24	3	[6, −2, 2] ⁴	Trunkerad tetraeder
3	3	12	3		Tietzes graf
3	3	36	3	[2, 6, −2, 6] ³
4	4	24	4	[−3, 3] ⁶ [3, −5, 5, −3, −5, 5] ²	G _{6, 2} , Y ₆	Yutsis 18j-symboletikett: B
3	4	4	4	[6, −3, 6, 6, 3, 6] ² [6, 6, −5, 5, 6, 6] ² [3, −3, 4, −3, 3, 4; –] [5, −3, 6, 6, 3, −5] ² [5, −3, −5, 4, 4, −5; –] [6, 6, −3, −5, 4, 4, 6, 6, −4, −4, 5, 3]		Yutsis 18j-symboletikett: L
3	4	8	4	[−4, 4, 4, 6, 6, −4] ² [6, −5, 5, −5, 5, 6] ² [4, −3, 3, 5, −4, −3; –] [−4, −4, 4, 4, −5, 5] ²		Yutsis 18j-symboletikett: K
3	4	2	4	[−4, 6, 3, 6, 6, −3, 5, 6, 4, 6, 6, −5] [−5, 4, 6, 6, 6, −4, 5, 5, 6, 6 , 6, −5] [5, −3, 4, 6, 3, −5, −4, −3, 3, 6, 3, −3] [4 , −4, 6, 4, −4, 5 , 5, −4, 6, 4, −5, −5] [4, −5, −3, 4, −4, 5, 3, −4, 5, −3, −5, 3]		Yutsis 18j-symboletikett: T
3	4	2	4	[3, 4, 5, -3, 5, -4; –] [3, 6, −4, −3, 4, 6] ² [−4, 5, 5, −4, 5, 5; –] [3, 6, −4, −3, 4, 4, 5, 6, −4, −4, 4, −5] [4, −5, 5, 6, −4, 5, 5, − 5, 5, 6, −5, −5] [4, −4, 5, −4, −4, 3, 4, −5, −3, 4, −4, 4]		Yutsis 18j-symboletikett: R
3	4	8	4	[4, −4, 6] ⁴ [3, 6, 3, −3, 6, −3] ² [−3, 6, 4, −4, 6, 3, −4, 6, −3, 3, 6, 4]	Bidiakis kub	Yutsis 18j-symboletikett: D
3	4	16	4	[6, −5, 5] ⁴ [3, 4, −4, −3, 4, −4] ²		Yutsis 18j-symboletikett: G
3	4	2	4	[−3, 5, −3, 4, 4, 5; –] [4, −5, 5, 6, −4, 6] ² [−3, 4, −3, 4, 4, −4; –] [5, 6, −3, −5, 4, −5, 3, 6, −4, −3, 5, 3] [5, 6, 4, −5, 5, −5, −4, 6, 3, −5, 5, −3]		Yutsis 18j-symboletikett: S
3	4	4	4	[4, -3, 4, 5, -4, 4; –] [4, 5, −5, 5, −4, 5; –] [−5, −3, 4, 5, −5, 4; –]		Yutsis 18j-symboletikett: N
3	4	2	4	[6, −4, 6, −4, 3, 5, 6, −3, 6, 4, −5, 4] [6, −4, 3, −4, 4, −3, 6, 3, − 4, 4, −3, 4] [5, 6, −4, 3, 5, −5, −3, 6, 3, −5, 4, −3] [ 5, −5, 4, 6, − 5, −5, −4, 3, 5, 6, −3, 5] [5, 5, −4, 4, 5, −5, −5, −4, 3, −5, 4, −3]		Yutsis 18j-symboletikett: V
3	4	4	4	[6, −3, 5, 6, −5, 3, 6, −5, −3, 6, 3, 5] [3, −4, 5, −3, 4, 6, 4, −5, − 4, 4, −4, 6]		Yutsis 18j-symboletikett: P
3	4	8	4	[5, 6, 6, −4, 5, −5, 4, 6, 6, −5, −4, 4]		Yutsis 18j-symboletikett: I
3	5	16	4	[4, −5, 4, −5, −4, 4; –]		Yutsis 18j-symboletikett: F
3	4	4	4	[6, 4, 6, 6, 6, −4] ² [−3, 4, −3, 5, 3, −4; –] [−5, 3, 6, 6, −3, 5, 5, 5, 6, 6, −5, −5] [−3, 3, 6, 4, −3, 5, 5, −4 , 6, 3, −5, −5]		Yutsis 18j-symboletikett: M
4	4	8	4	[3, 5, 5, -3, 5, 5; –] [−3, 5, −3, 5, 3, 5; –] [5, −3, 5, 5, 5, −5; –]		Yutsis 18j-symboletikett: E
3	4	48	4	[5, −5, −3, 3] ³ [−5, 5] ⁶	Franklin graf	Yutsis 18j-symboletikett: C
3	4	24	4	[6] ¹² [6, 6, −3, −5, 5, 3] ²		Yutsis 18j-symboletikett: A
3	5	18	4	[6, −5, −4, 4, −5, 4, 6, −4, 5, −4, 4, 5]		Yutsis 18j-symboletikett: H

LCF-posterna saknas ovan om grafen inte har någon Hamiltonsk cykel , vilket är sällsynt (se Taits gissning ) . I detta fall fungerar en lista med kanter mellan par av hörn märkta 0 till n−1 i den tredje kolumnen som en identifierare.

Vektorkopplingskoefficienter

Varje 4-kopplad (i ovanstående mening) enkel kubisk graf på $2 n$ hörn definierar en klass av kvantmekaniska $3 n$ -j symboler. Grovt sett representerar varje vertex en 3-jm-symbol , grafen omvandlas till en digraf genom att tilldela tecken till vinkelmomentumkvanttalen $j$ , hörnen är märkta med en handenhet som representerar ordningen av de tre $j$ (av de tre kanterna) i 3-jm-symbolen, och grafen representerar en summa över produkten av alla dessa tal som är tilldelade hörnen.

Det finns 1 ( 6-j ), 1 ( 9-j ), 2 (12-j), 5 (15-j), 18 (18-j), 84 (21-j), 607 (24-j) , 6100 (27-j), 78824 (30-j), 1195280 (33-j), 20297600 (36-j), 376940415 (39-j) etc. av dessa (sekvens A175847 i OEIS ) .

Om de är ekvivalenta med vissa vertex-inducerade binära träd (att skära en kant och hitta ett snitt som delar upp den återstående grafen i två träd), är de representationer av återkopplingskoefficienter, och är då också kända som Yutsis-grafer (sekvens A111916 i OEIS ) ).

Se även

Yutsis, AP ; Levinson, IB; Vanagas, VV; Sen, A. (1962). Matematisk apparat för teorin om rörelsemängd . Israels program för vetenskapliga översättningar. Bibcode : 1962mata.book.....Y .
Massot, J.-N.; El-Baz, E.; Lafoucriere, J. (1967). "En allmän grafisk metod för vinkelmomentum". Recensioner av modern fysik . 39 (2): 288–305. Bibcode : 1967RvMp...39..288M . doi : 10.1103/RevModPhys.39.288 .
Bussemaker, FC; Cobeljic, S.; Cvetkovic, DM (1976). "Datorundersökningar av kubikgrafer" (PDF) .
Bussemaker, FC; Cobeljic, S.; Cvetkovic, DM; Seidel, JJ (1977). "Kubiska grafer på <=14 hörn" . J. Combin. Teori Ser. B . 23 (2–3): 234–235. doi : 10.1016/0095-8956(77)90034-X .
Frucht, R. (1977). "En kanonisk representation av trivalenta Hamiltonian grafer". Journal of Graph Theory . 1 (1): 45–60. doi : 10.1002/jgt.3190010111 . MR 0463029 .
Clark, L.; Entringer, R. (1983). "Minsta maximalt icke-hamiltonska grafer". Per. Mathem. Ungern . 14 (1): 57–68. doi : 10.1007/BF02023582 . MR 0697357 . S2CID 122218690 .
Wormald, NC (1985). "Uppräkning av cykliskt 4-kopplade kubikdiagram". Journal of Graph Theory . 9 (4): 563–573. doi : 10.1002/jgt.3190090418 . MR 0890248 .
Bar-Shalom, A.; Klapisch, M. (1988). "NJGRAF - ett effektivt program för beräkning av allmänna återkopplingskoefficienter genom grafisk analys, kompatibelt med NJSYM". Comput. Phys. Commun . 50 (3): 375–393. Bibcode : 1988CoPhC..50..375B . doi : 10.1016/0010-4655(88)90192-0 .
Brinkmann, G. (1996). "Snabb generering av kubikgrafer". Journal of Graph Theory . 23 (2): 139–149. doi : 10.1002/(SICI)1097-0118(199610)23:2<139::AID-JGT5>3.0.CO;2-U . MR 1408342 .
Fack, V.; Pitre, SN; Van der Jeugt, J. (1997). "Beräkning av allmänna återkopplingskoefficienter med hjälp av grafiska metoder". Comput. Phys. Commun . 101 (1–2): 155–170. Bibcode : 1997CoPhC.101..155F . doi : 10.1016/S0010-4655(96)00170-1 .
Danos, M.; Fano, U. (1998). "Grafisk analys av rörelsemängd för kollisionsprodukter". Fysiska rapporter . 304 (4): 155–227. Bibcode : 1998PhR...304..155D . doi : 10.1016/S0370-1573(98)00020-9 .
Meringer, M. (1999). "Snabb generering av vanliga grafer och konstruktion av burar". Journal of Graph Theory . 30 (2): 137–146. doi : 10.1002/(SICI)1097-0118(199902)30:2<137::AID-JGT7>3.0.CO;2-G . MR 1665972 .
Van Dyck, D.; Brinkmann, G.; Fack, V.; McKay, BD (2005). "Att vara eller inte vara Yutsis: Algoritmer för beslutsproblemet". Comput. Phys. Commun . 173 (1–2): 61–70. Bibcode : 2005CoPhC.173...61V . doi : 10.1016/j.cpc.2005.07.008 . MR 2179511 .
Van Dyck, D.; Fack, V. (2007). "Om minskningen av Yutsis-grafer" . Diskret matematik . 307 (11–12): 1506–1515. doi : 10.1016/j.disc.2005.11.088 . MR 2311125 .
Aldred, REL; Van Dyck, D.; Brinkmann, G.; Fack, V.; McKay, BD (2009). "Grafisera strukturella egenskaper hos icke-Yutsis-grafer som möjliggör snabb igenkänning". Diskret matematik . 157 (2): 377–386. doi : 10.1016/j.dam.2008.03.020 . hdl : 1942/9184 . MR 2479811 .
Mathar, Richard J. (2011). "The Wigner plottar upp till 12 hörn". arXiv : 1109.2358 [ math-ph ].