Dürer graf
Inom det matematiska området grafteori är Dürer -grafen en oriktad graf med 12 hörn och 18 kanter. Den är uppkallad efter Albrecht Dürer , vars gravyr från 1514 Melencolia I inkluderar en skildring av Dürers fasta kropp , en konvex polyeder med Dürergrafen som sitt skelett . Dürers solid är en av endast fyra vältäckta enkla konvexa polyedrar.
Dürer är stabil
Dürers solid är kombinatoriskt likvärdig med en kub med två motsatta hörn trunkerade , även om Dürers skildring av det inte är i denna form utan snarare som en trunkerad rhombohedron eller triangulär trunkerad trapets . Den exakta geometrin hos det fasta materialet som avbildas av Dürer är föremål för en del akademisk debatt, med olika hypotetiska värden för dess spetsiga vinklar som sträcker sig från 72° till 82°.
Grafteoretiska egenskaper
| Dürer-grafen | |
|---|---|
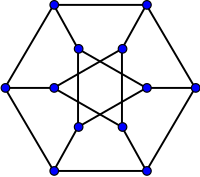 Dürer-grafen
| |
| Döpt efter | Albrecht Dürer |
| Vertices | 12 |
| Kanter | 18 |
| Radie | 3 |
| Diameter | 4 |
| Omkrets | 3 |
| Automorfismer | 12 (D 6 ) |
| Kromatiskt nummer | 3 |
| Kromatiskt index | 3 |
| Egenskaper |
Cubic Planar vältäckt |
| Tabell över grafer och parametrar | |
Dürer-grafen är den graf som bildas av hörnen och kanterna på Dürer-kroppen. Det är en kubisk graf med omkrets 3 och diameter 4. Förutom dess konstruktion som skelettet av Dürers fasta kropp, kan den erhållas genom att applicera en Y-Δ-transform på de motsatta hörnen av en kubgraf , eller som den generaliserade Petersen-grafen G (6,2). Som med vilken graf som helst av en konvex polyeder , är Dürer-grafen en enkel plan graf med 3 vertex .
Dürer-grafen är en vältäckt graf , vilket betyder att alla dess maximala oberoende uppsättningar har samma antal hörn, fyra. Det är en av fyra vältäckta kubiska polyedriska grafer och en av sju vältäckta 3-kopplade kubiska grafer. De enda andra tre vältäckta enkla konvexa polyedrarna är tetraedern , det triangulära prismat och det femkantiga prismat .
Dürer-grafen är Hamiltonsk , med LCF-notation [-4,5,2,-4,-2,5;-]. Mer exakt, den har exakt sex Hamilton-cykler, av vilka varje par kan mappas in i varandra genom en symmetri av grafen.
Symmetrier
Automorfismgruppen både i Dürer-grafen och Dürer-fastämnet (i antingen den trunkerade kubformen eller den form som visas av Dürer) är isomorf till den dihedriska gruppen av ordningen 12 : D 6 .
Galleri
Det kromatiska indexet för Dürer-grafen är 3.
Det kromatiska numret på Dürer-grafen är 3.
Dürer-grafen är Hamiltonsk .
Anteckningar
- Campbell, SR; Ellingham, MN ; Royle, Gordon F. (1993), "A characterization of well-covered cubic graphs", Journal of Combinatorial Mathematics and Combinatorial Computing , 13 : 193–212, MR 1220613 .
- Campbell, Stephen R.; Plummer, Michael D. (1988), "On well-covered 3-polytopes", Ars Combinatoria , 25 (A): 215–242, MR 0942505 .
- Castagna, Frank; Prins, Geert (1972), "Every Generalized Petersen Graph has a Tait Coloring", Pacific Journal of Mathematics , 40 : 53–58, doi : 10.2140/pjm.1972.40.53 .
- Schwenk, Allen J. (1989), "Enumeration of Hamiltonian cycles in certain generalized Petersen graphs", Journal of Combinatorial Theory , Series B, 47 (1): 53–59, doi : 10.1016/0095-8956(89)90064- 6 , MR 1007713 .
- Weber, P. (1900), Beiträge zu Dürers Weltanschauung—Eine Studie über die drei Stiche Ritter, Tod und Teufel, Melancholie und Hieronymus im Gehäus , Strassburg . Som citeras av Weitzel (2004) .
- Weitzel, Hans (2004), "A further hypothesis on the polyhedron of A. Dürers gravyr Melencolia I", Historia Mathematica , 31 (1): 11–14, doi : 10.1016/S0315-0860(03)00029-6 .