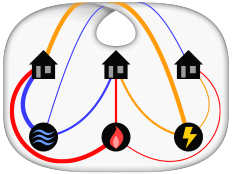
Problem med tre verktyg

"Vatten, gas och elektricitet" omdirigerar här. För verktygen, se Allmän nytta . För romanen Sewer, Gas & Electric, se Matt Ruff .

Diagram över de tre verktygsproblemen som visar linjer i ett plan. Kan varje hus anslutas till varje nytta, utan att anslutningslinjer korsar?

Två vyer av verktygsgrafen, även känd som Thomsen-grafen eller $K_{3,3}$

Det klassiska matematiska pusslet, känt som problemet med de tre verktygen eller ibland vatten, gas och elektricitet, kräver att förbindelser mellan tre hus och tre allmännyttiga företag i planet ska dras . När han ställde upp det i början av 1900-talet Henry Dudeney att det redan var ett gammalt problem. Det är ett omöjligt pussel : det är inte möjligt att ansluta alla nio linjerna utan att korsa. Versioner av problemet på icke-plana ytor som en torus eller Möbius-remsa , eller som tillåter anslutningar att passera genom andra hus eller verktyg, kan lösas.

Detta pussel kan formaliseras som ett problem i topologisk grafteori genom att fråga om den fullständiga tvådelade grafen ${\displaystyle K_{3,3}} ,$ med hörn som representerar husen och verktyg och kanter som representerar deras anslutningar, har en graf inbäddning i planet. Pusslets omöjlighet motsvarar det faktum att $K_{3,3}$ inte är en plan graf . Flera bevis för denna omöjlighet är kända och utgör en del av beviset för Kuratowskis sats som karakteriserar plana grafer med två förbjudna subgrafer, varav en är $K_{3,3}$ . Frågan om att minimera antalet korsningar i ritningar av kompletta tvådelade grafer är känd som Turáns tegelfabriksproblem , och för $K_{3,3}$ är det minsta antalet korsningar en.

$K_{3,3}$ är en graf med sex hörn och nio kanter, ofta kallad verktygsgrafen med hänvisning till problemet. Den har också kallats Thomsen-grafen efter 1800-talets kemist Julius Thomsen . Det är en väl täckt graf , den minsta triangelfria kubiska grafen och den minsta icke-plana minimalt stela grafen .

Historia

En genomgång av historien om de tre verktygsproblemen ges av Kullman (1979) . Han konstaterar att de flesta publicerade referenser till problemet karakteriserar det som "mycket urgammalt". I den tidigaste publikationen som hittats av Kullman, kallar Henry Dudeney ( 1917 ) det "vatten, gas och elektricitet". Dudeney säger dock att problemet är "lika gammalt som kullarna...mycket äldre än elektrisk belysning , eller till och med gas ". Dudeney publicerade också samma pussel tidigare, i The Strand Magazine 1913. Ett konkurrerande anspråk på prioritet går till Sam Loyd , som citerades av sin son i en postum biografi för att ha publicerat problemet 1900.

En annan tidig version av problemet handlar om att koppla tre hus till tre brunnar. Det anges på samma sätt som ett annorlunda (och lösbart) pussel som också involverar tre hus och tre fontäner, där alla tre fontäner och ett hus rör vid en rektangulär vägg; pusslet innebär återigen att göra icke-korsande förbindelser, men bara mellan tre utpekade par av hus och brunnar eller fontäner, som i moderna nummerlänkpussel . Loyds pussel "The Quarrelsome Neighbors" involverar på liknande sätt att ansluta tre hus till tre portar med tre icke-korsande stigar (snarare än nio som i verktygsproblemet); ett hus och de tre portarna är på väggen av en rektangulär gård, som innehåller de andra två husen inom den.

Liksom i problemet med tre verktyg förekommer grafen ${\displaystyle K_{3,3}} i$ publikationer från slutet av 1800-talet och början av 1900-talet både i tidiga studier av strukturell stelhet och i kemisk grafteori , där Julius Thomsen föreslog det 1886 för den då osäkra strukturen av bensen . För att hedra Thomsens arbete kallas ${\displaystyle K_{3,3}} ibland Thomsen-grafen.$

Påstående

De tre verktygsproblemen kan anges på följande sätt:

Anta att tre hus vardera behöver anslutas till vatten-, gas- och elbolagen, med en separat linje från varje hus till varje företag. Finns det något sätt att göra alla nio anslutningarna utan att någon av linjerna korsar varandra?

Problemet är ett abstrakt matematiskt pussel som lägger på begränsningar som inte skulle existera i en praktisk ingenjörssituation. Dess matematiska formalisering är en del av området topologisk grafteori som studerar inbäddningen av grafer på ytor . En viktig del av pusslet, men en som ofta inte uttryckligen anges i informella formuleringar av pusslet, är att husen, företagen och linjerna alla måste placeras på en tvådimensionell yta med ett plans topologi, och att ledningarna får inte passera genom andra byggnader; ibland genomförs detta genom att visa en ritning av husen och företagen, och be om att anslutningarna ska ritas som linjer på samma ritning.

I mer formella grafteoretiska termer frågar problemet om den fullständiga tvådelade grafen $K_{3,3}$ är en plan graf . Den här grafen har sex hörn i två delmängder av tre: en hörn för varje hus och en för varje verktyg. Den har nio kanter, en kant för var och en av parningarna av ett hus med ett verktyg, eller mer abstrakt en kant för varje par av en vertex i en delmängd och en vertex i den andra delmängden. Plana grafer är de grafer som kan ritas utan korsningar i planet, och om en sådan ritning kunde hittas skulle det lösa tre verktygspusslet.

Pussellösningar

Olöslighet

Bevis utan ord : Ett hus är tillfälligt raderat. Linjerna som förbinder de återstående husen med verktygen delar upp planet i tre regioner. Oavsett vilken region det raderade huset placeras i, är det liknande skuggade verktyget utanför regionen. Vid Jordan-kurvans teorem måste en linje som förbinder dem skära en av de befintliga linjerna.

Som det vanligtvis presenteras (på ett platt tvådimensionellt plan) är lösningen på nyttopusslet "nej": det finns inget sätt att göra alla nio kopplingarna utan att någon av linjerna korsar varandra. Med andra ord är grafen $K_{3,3}$ inte plan. Kazimierz Kuratowski konstaterade 1930 att $K_{3,3}$ är icke-planär, varav det följer att problemet inte har någon lösning. Kullman (1979) menar dock att "Intressant nog publicerade Kuratowski inte ett detaljerat bevis på att [ ${\displaystyle K_{3,3}} ]$ är icke-planärt".

Ett bevis på omöjligheten att hitta en plan inbäddning av $K_{3,3}$ använder en fallanalys som involverar Jordan-kurvans sats . I denna lösning undersöker man olika möjligheter för placeringen av hörnen med avseende på grafens 4-cykler och visar att de alla är inkonsekventa med en plan inbäddning.

Alternativt är det möjligt att visa att vilken brolös tvådelad plan graf som helst med $V$ hörn och $E$ kanter har $E\leq 2V-4$ genom att kombinera Euler formel $V-E+F=2$ (där $F$ är antalet ytor i en plan inbäddning) med observation att antalet ytor är högst hälften av antal kanter (topparna runt varje yta måste växla mellan hus och verktyg, så varje yta har minst fyra kanter, och varje kant tillhör exakt två ytor). I verktygsgrafen är $E=9$ och $2V-4=8$ så i verktygsgrafen är det inte sant att $E \leq 2V-4$ . Eftersom den inte uppfyller denna ojämlikhet, kan nyttografen inte vara plan.

Att ändra reglerna

Lösning på en torus

Lösning på en Möbius-remsa

$K_{3,3}$ är en toroidal graf , vilket betyder att den kan bäddas in utan korsningar på en torus , en yta av genus ett. Dessa inbäddningar löser versioner av pusslet där husen och företagen ritas på en kaffemugg eller annan sådan yta istället för ett platt plan. Det finns till och med tillräckligt med ytterligare frihet på torus för att lösa en version av pusslet med fyra hus och fyra verktyg. På liknande sätt, om pusslet med tre verktyg presenteras på ett ark av ett genomskinligt material, kan det lösas efter vridning och limning av arket för att bilda en Möbius-remsa .

Ett annat sätt att ändra pusslets regler som skulle göra det lösbart, föreslagit av Henry Dudeney , är att tillåta ledningar att passera genom andra hus eller ledningar än de som de ansluter.

Egenskaper för verktygsdiagrammet

Bortom nyttopusslet kommer samma graf ${\displaystyle K_{3,3}} upp i flera andra matematiska sammanhang, inklusive$ stelhetsteori , klassificering av burar och vältäckta grafer , studiet av grafkorsande tal , och teorin om grafen minor .

Stelhet

Verktygsgrafen $K_{3,3}$ är en Laman-graf , vilket betyder att för nästan alla placeringar av dess hörn i planet, finns det inget sätt att kontinuerligt flytta dess hörn samtidigt som alla kantlängder bevaras, annat än genom en stel rörelse av hela planet, och att ingen av dess spännande subgrafer har samma styvhetsegenskap . Det är det minsta exemplet på en icke-plan Laman-graf. Trots att den är en minimal stel graf, har den icke-styva inbäddningar med speciella placeringar för sina hörn. För generella positionsinbäddningar har en polynomekvation som beskriver alla möjliga placeringar med samma kantlängder grad 16, vilket betyder att det i allmänhet kan finnas högst 16 placeringar med samma längder. Det är möjligt att hitta system med kantlängder för vilka upp till åtta av lösningarna till denna ekvation beskriver realiserbara placeringar.

Andra grafteoretiska egenskaper

$K_{3,3}$ är en triangelfri graf , där varje vertex har exakt tre grannar (en kubisk graf ) . Bland alla sådana grafer är det den minsta. Därför är det (3,4)-buren , den minsta grafen som har tre grannar per vertex och där den kortaste cykeln har längd fyra.

Liksom alla andra kompletta tvådelade grafer är det en väl täckt graf , vilket betyder att varje maximal oberoende uppsättning har samma storlek. I denna graf är de enda två maximala oberoende uppsättningarna de två sidorna av bipartitionen och är lika stora. $K_{3,3}$ är en av endast sju 3-regelbundna 3-kopplade vältäckta grafer.

Generaliseringar

Ritning av $K_{3,3}$ med en korsning

Två viktiga karakteriseringar av plana grafer, Kuratowskis teorem att de plana graferna är exakt de grafer som varken innehåller $K_{3,3}$ eller hela grafen $K_{5}$ som en underavdelning, och Wagners teorem att de plana graferna är exakt de grafer som varken innehåller $K_{3,3}$ eller $K_{5}$ som moll , använder och generaliserar icke-planariteten av $K_{3,3}$ .

Pál Turáns " tegelfabriksproblem " ber mer generellt om en formel för det minsta antalet korsningar i en ritning av den fullständiga tvådelade grafen $K_{a,b}$ i termer av antalet hörn $a$ och $b$ på två sidor av bipartitionen. Verktygsgrafen $K_{3,3}$ kan ritas med endast en korsning, men inte med nollkorsningar, så dess korsningsnummer är ett.

externa länkar

• 3 Utilities Pussel vid Cut-the-knoten
• Verktygspusslet förklarat och "löst" på Archimedes-lab.org
• Weisstein, Eric W. , "Utility graph" , MathWorld