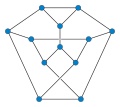
Tietzes graf
| Tietzes graf | |
|---|---|
 Tietze-grafen
| |
| Vertices | 12 |
| Kanter | 18 |
| Radie | 3 |
| Diameter | 3 |
| Omkrets | 3 |
| Automorfismer | 12 ( D 6 ) |
| Kromatiskt nummer | 3 |
| Kromatiskt index | 4 |
| Egenskaper |
Cubic Snark |
| Tabell över grafer och parametrar | |
Inom det matematiska området grafteorin är Tietzes graf en oriktad kubisk graf med 12 hörn och 18 kanter . Den är uppkallad efter Heinrich Franz Friedrich Tietze , som 1910 visade att Möbiusremsan kan delas in i sex regioner som alla berör varandra – tre längs remsans gräns och tre längs dess mittlinje – och därför att grafer som är inbäddade på Möbius-remsan kan kräva sex färger . Gränssegmenten för regionerna i Tietzes underavdelning (inklusive segmenten längs gränsen för själva Möbiusremsan) bildar en inbäddning av Tietzes graf.
Relation till Petersen graf
Tietzes graf kan bildas från Petersen-grafen genom att ersätta en av dess hörn med en triangel . Liksom Tietze-grafen, bildar Petersen-grafen gränsen för sex ömsesidigt berörande regioner, men på det projektiva planet snarare än på Möbius-remsan. Om man skär ett hål från denna underavdelning av det projektiva planet, som omger en enda vertex, ersätts den omgivna vertexen av en triangel av regiongränser runt hålet, vilket ger den tidigare beskrivna konstruktionen av Tietze-grafen.
Hamiltonicitet
Både Tietzes graf och Petersen-grafen är maximalt icke-hamiltonska : de har ingen Hamiltonsk cykel , men vilka två icke-angränsande hörn som helst kan kopplas samman med en Hamiltonsk bana. Tietzes graf och Petersen-grafen är de enda kubiska icke-Hamiltoniska graferna med 2 hörn anslutna med 12 eller färre hörn.
Till skillnad från Petersen-grafen är Tietzes graf inte hypohamiltonsk : om man tar bort en av dess tre triangelhörna bildas en mindre graf som förblir icke-hamiltonsk.
Kantfärgning och perfekta matchningar
Kantfärgning Tietzes graf kräver fyra färger; det vill säga dess kromatiska index är 4. På motsvarande sätt kan kanterna på Tietzes graf delas upp i fyra matchningar , men inte färre.
Tietzes graf matchar en del av definitionen av en snark : det är en kubisk brolös graf som inte är 3-kantsfärgbar. De flesta författare begränsar dock snarks till grafer utan 3-cykler, så Tietzes graf anses generellt inte vara en snark. Ändå är den isomorf till grafen J 3 , en del av en oändlig familj av blomsnarkar som introducerades av R. Isaacs 1975.
Till skillnad från Petersen-grafen kan Tietze-grafen täckas av fyra perfekta matchningar . Denna egenskap spelar en nyckelroll i ett bevis på att testet om en graf kan täckas av fyra perfekta matchningar är NP-komplett .
Ytterligare egenskaper
Tietzes graf har kromatiskt nummer 3, kromatiskt index 4, omkrets 3 och diameter 3. Oberoendetalet är 5. Dess automorfismgrupp har ordning 12 och är isomorf till den dihedriska gruppen D 6 , gruppen av symmetrier för en hexagon , inklusive båda rotationer och reflektioner. Denna grupp har två banor av storlek 3 och en av storlek 6 på hörn, och därför är denna graf inte vertextransitiv .
Galleri
Det kromatiska numret på Tietze-grafen är 3.
Det kromatiska indexet för Tietze-grafen är 4.
Tietze-grafen har korsning nummer 2 och är 1-plan .
Se även
- Dürer-graf och Franklin-graf , två andra kubikgrafer med 12 vertex