Stympad rhombicuboctahedron
| Stympad rhombicuboctahedron | |
|---|---|

|
|
| Schläfli symbol | trr{4,3} = |
| Conway notation | taaC |
| Ansikten |
50: 24 {4} 8 {6} 6+12 {8} |
| Kanter | 144 |
| Vertices | 96 |
| Symmetrigrupp | Åh , [4,3], (*432) ordning 48 |
| Rotationsgrupp | O, [4,3] + , (432), ordning 24 |
| Dubbel polyeder | Disdyakis icositetrahedron
|
| Egenskaper | konvex, zonoeder |
Den trunkerade rhombicuboctahedronen är en polyeder , konstruerad som en trunkering av rhombicuboctahedronen . Den har 50 ansikten bestående av 18 oktagoner, 8 hexagoner och 24 rutor. Den kan fylla utrymmet med den stympade kuben , den stympade tetraedern och det triangulära prismat som en stympad runkisk kubisk honungskaka .
Andra namn
- Stympad liten rhombicuboctahedron
- Fasad cuboctahedron
Zonohedron
Som en zonohedron kan den konstrueras med alla utom 12 oktagoner som vanliga polygoner . Den har två uppsättningar av 48 hörn som finns på två avstånd från dess centrum.
Det representerar Minkowski summan av en kub , en trunkerad oktaeder och en rombisk dodekaeder .
Utgrävd stympad rhombicuboctahedron
| Utgrävd stympad rhombicuboctahedron | |
|---|---|
| Ansikten |
148: 8 {3} 24+96+6 {4} 8 {6} 6 {8} |
| Kanter | 312 |
| Vertices | 144 |
| Euler-karaktär | -20 |
| Släkte | 11 |
| Symmetrigrupp | Åh , [4,3], (*432) ordning 48 |
Den utgrävda trunkerade rhombicuboctahedron är en toroidal polyeder , konstruerad av en trunkerad rhombicuboctahedron med dess 12 oregelbundna oktagonala ytor borttagna. Den består av ett nätverk av 6 kvadratiska kupoler , 8 triangulära kupoler och 24 triangulära prismor . Den har 148 ytor (8 trianglar, 126 kvadrater, 8 hexagoner och 6 oktagoner), 312 kanter och 144 hörn. Med Euler-karakteristiken χ = f + v - e = -20 är dess släkte (g = (2-χ)/2) 11.
Utan de triangulära prismorna blir den toroidformade polyedern en stympad cuboctahedron.

|
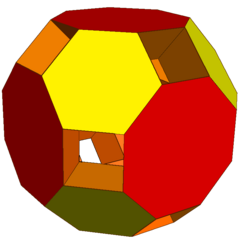
|
| Stympad rhombicuboctahedron | Stympad cuboctahedron |
|---|
Besläktade polyedrar
Den trunkerade kuboktaedern är liknande, med alla regelbundna ytor och 4.6.8 vertexfigur .
Triangeln och kvadraterna av rhombicuboctahedron kan oberoende rätas eller trunkeras, vilket skapar fyra permutationer av polyedrar. De delvis trunkerade formerna kan ses som kantsammandragningar av den trunkerade formen.
Den trunkerade rhombicuboctahedronen kan ses i sekvens av rektifikations- och trunkeringsoperationer från cuboctahedron . Ett ytterligare alterneringssteg leder till den snubbade rhombicuboctahedronen .
| namn | r{4,3} | rr{4,3} | tr{4,3} |
Rättad rrr{4,3} |
Delvis stympad |
Trunkerad trr{4,3} |
srCO | |
|---|---|---|---|---|---|---|---|---|
| Conway | aC | aaC=eC | taC=bC | aaaC=eaC | dXC | dXdC | taaC=baC | säck |
| Bild |

|

|
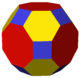
|

|

|

|

|

|
| VertFigs | 3.4.3.4 | 3.4.4.4 | 4.6.8 |
4.4.4. 4 d och 3.4.4 d .4 |
4.4.4. 6i _ och 4.6.6i _ |
4.6 i .8 och 3.4.6 i .4 |
4.8. 8 p och 4.6.8 p |
3.3.3.3.4 och 3.3.4.3.4 |
Se även
- Eppstein, David (1996). "Zonoedrar och zonotoper" . Mathematica in Education and Research . 5 (4): 15–21.
- Coxeter Regular Polytopes , tredje upplagan, (1973), Dover upplagan, ISBN 0-486-61480-8 (s. 145–154 Kapitel 8: Trunkering)
- John H. Conway , Heidi Burgiel, Chaim Goodman-Strauss , The Symmetries of Things 2008, ISBN 978-1-56881-220-5
externa länkar
- George Harts Conway-tolkare : genererar polyedrar i VRML och tar Conway-notation som indata
- Prismaexpansions [1] Toroidmodell
