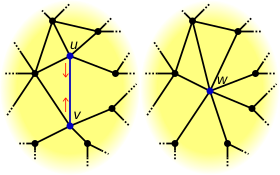
Kantkontraktion

Sammandragning av kanten mellan de angivna hörnen, vilket resulterar i grafen G / {uv}.

I grafteorin är en kantkontraktion en operation som tar bort en kant från en graf samtidigt som de två hörn som den tidigare sammanfogade sammanfogas. Kantsammandragning är en grundläggande operation i teorin om grafiska biträden . Vertexidentifiering är en mindre restriktiv form av denna operation.

Definition

Kantkontraktionsoperationen sker i förhållande till en viss kant, e $\displaystyle e}$ . Kanten $e$ tas bort och dess två infallande hörn, $u$ och $v$ , slås samman till en ny vertex $w$ , där kanterna faller in på ${ \displaystyle w}$ motsvarar var och en av en kantincident till antingen $u$ eller $v$ . Mer generellt kan operationen utföras på en uppsättning kanter genom att dra ihop varje kant (i valfri ordning).

Den resulterande inducerade grafen skrivs ibland som $G/e$ . (Själa detta med $G\setminus e$ , vilket innebär att man tar bort kanten $e$ .)

Dra ihop en kant utan att skapa flera kanter.

Som definieras nedan kan en kantkontraktionsoperation resultera i en graf med flera kanter även om den ursprungliga grafen var en enkel graf . Vissa författare tillåter dock inte skapandet av flera kanter, så att kantsammandragningar utförda på enkla grafer alltid ger enkla grafer.

Formell definition

Låt $G=(V,E)$ vara en graf ( eller riktad graf ) som innehåller en kant $e=(u,v)$ med $u\neq v$ . Låt $f$ vara en funktion som mappar varje vertex i $V\setminus \{u,v\}$ till sig själv, och annars mappar det till ett nytt vertex ${ \displaystyle w}$ . Sammandragningen av $e$ resulterar i en ny graf $G'=(V',E')$ , där ${\displaystyle V'=(V\setminus \{u,v\})\cup \{w\}} ,$ E $\displaystyle E'=E\setminus \{e\}}$ , och för varje $x\in V$ , $x'=f(x)\in V'$ hänför sig till en kant $e'\in E'$ om och endast om, motsvarande kant, $e\in E$ faller samman med $x$ i ${\ displaystil G}$ .

Vertex identifiering

Vertexidentifiering (kallas ibland vertexkontraktion ) tar bort begränsningen att sammandragningen måste ske över hörn som delar en infallande kant. (Därför är kantkontraktion ett specialfall av vertexidentifiering.) Operationen kan ske på vilket par (eller delmängder) som helst av hörn i grafen. Kanter mellan två sammandragande hörn tas ibland bort. Om $v$ och $v'$ är hörn av distinkta komponenter i $G$ , då kan vi skapa en ny graf $G'$ genom att identifiera $v$ och $v'$ i $G$ som en ny vertex ${\textbf {v}}$ i $G'$ . Mer generellt, givet en partition av vertexuppsättningen, kan man identifiera hörn i partitionen; den resulterande grafen kallas en kvotgraf .

Vertexklyvning

Vertex-klyvning , vilket är samma sak som vertexdelning, betyder att en vertex delas i två, där dessa två nya hörn ligger intill de hörn som den ursprungliga vertexen låg intill. Detta är en omvänd operation av vertexidentifiering, även om i allmänhet för vertexidentifiering är angränsande hörn av de två identifierade hörnen inte samma uppsättning.

Bansammandragning

Bansammandragning sker på uppsättningen kanter i en bana som drar ihop sig för att bilda en enda kant mellan banans ändpunkter. Kanter som faller på hörn längs banan elimineras antingen eller är godtyckligt (eller systematiskt) kopplade till en av ändpunkterna.

Vridning

Betrakta två disjunkta grafer $G_{1}$ och $G_{2}$ , där $G_{1}$ innehåller hörn $u_{1}$ och $v_{1}$ och $G_{2}$ innehåller hörn $u_{2}$ och $v_{2}$ . Antag att vi kan erhålla grafen $G$ genom att identifiera hörnen $u_{1}$ i $G_{1}$ och $u_{2}$ i $G_{2}$ som vertex $u$ i $G$ och identifierar hörn $v_{1}$ i $G_{1}$ och $v_{2}$ av $G_{2}$ som vertex $v$ av $G$ . I ett vridande $G'$ av $G$ med avseende på vertexmängden $\{u,v\}$ identifierar vi istället ${\ displaystyle u_{1}}$ med $v_{2}$ och $v_{1}$ med $u_{2}$ .

Ansökningar

Både kant- och vertexkontraktionstekniker är värdefulla i bevis genom induktion på antalet hörn eller kanter i en graf, där det kan antas att en egenskap gäller för alla mindre grafer och detta kan användas för att bevisa egenskapen för den större grafen.

Kantkontraktion används i den rekursiva formeln för antalet spännande träd i en godtyckligt sammankopplad graf och i återkommande formel för det kromatiska polynomet i en enkel graf.

Sammandragningar är också användbara i strukturer där vi vill förenkla en graf genom att identifiera hörn som representerar väsentligen likvärdiga enheter. Ett av de vanligaste exemplen är reduktionen av en allmän riktad graf till en acyklisk riktad graf genom att dra ihop alla hörn i varje starkt ansluten komponent . Om relationen som beskrivs av grafen är transitiv går ingen information förlorad så länge vi märker varje vertex med uppsättningen etiketter för de hörn som dras ihop för att bilda den.

Ett annat exempel är koalesceringen som utförs i global graffärgsregisterallokering , där hörn dras samman (där det är säkert) för att eliminera flyttoperationer mellan distinkta variabler.

Kantkontraktion används i 3D-modelleringspaket (antingen manuellt eller genom någon funktion i modelleringsprogramvaran) för att konsekvent minska vertexantalet, vilket hjälper till att skapa modeller med låg polygon.

Se även

• Underavdelning (grafteori)

Anteckningar

•   Gross, Jonathan; Yellen, Jay (1998), Graph Theory and its applications , CRC Press, ISBN 0-8493-3982-0
•   Oxley, James (2006) [1992], Matroid Theory , Oxford University Press, ISBN 978-0-19-920250-8
•   Rosen, Kenneth (2011), Diskret matematik och dess tillämpningar (7:e upplagan), McGraw-Hill, ISBN 978-0-07-338309-5
•   West, Douglas B. (2001), Introduction to Graph Theory (2:a upplagan), Prentice-Hall, ISBN 0-13-014400-2

externa länkar

• Weisstein, Eric W. "Kantsammandragning" . MathWorld .