Modularitet (nätverk)

För annan användning, se Modularitet .

Exempel på modularitetsmätning och färgning på ett skalfritt nätverk .

Modularitet är ett mått på strukturen hos nätverk eller grafer som mäter styrkan i uppdelningen av ett nätverk i moduler (även kallade grupper, kluster eller gemenskaper). Nätverk med hög modularitet har täta kopplingar mellan noderna inom moduler men glesa kopplingar mellan noder i olika moduler. Modularitet används ofta i optimeringsmetoder för att upptäcka gemenskapsstruktur i nätverk. Det har dock visat sig att modularitet lider av en upplösningsgräns och att den därför inte kan upptäcka små samhällen. Biologiska nätverk, inklusive djurhjärnor, uppvisar en hög grad av modularitet.

Motivering

Många vetenskapligt viktiga problem kan representeras och empiriskt studeras med hjälp av nätverk. Till exempel är biologiska och sociala mönster, World Wide Web, metaboliska nätverk, näringsnät, neurala nätverk och patologiska nätverk verkliga problem som kan representeras matematiskt och topologiskt studeras för att avslöja några oväntade strukturella egenskaper. De flesta av dessa nätverk har en viss gemenskapsstruktur som har stor betydelse för att bygga upp en förståelse för nätverkets dynamik. Till exempel kommer en nära ansluten social gemenskap att innebära en snabbare överföring av information eller rykten bland dem än en löst ansluten gemenskap. Således, om ett nätverk representeras av ett antal individuella noder sammankopplade med länkar som betecknar en viss grad av interaktion mellan noderna, definieras gemenskaper som grupper av tätt sammankopplade noder som endast är sparsamt sammankopplade med resten av nätverket. Därför kan det vara absolut nödvändigt att identifiera gemenskaperna i nätverk eftersom gemenskaperna kan ha helt olika egenskaper såsom nodgrad, klustringskoefficient, mellanhet, centralitet. etc. från det genomsnittliga nätet. Modularitet är en sådan åtgärd, som när den maximeras leder till uppkomsten av gemenskaper i ett givet nätverk.

Definition

Modularitet är andelen av kanterna som faller inom de givna grupperna minus den förväntade andelen om kanterna fördelades slumpmässigt. Värdet på modulariteten för oviktade och oriktade grafer ligger i området $[-1/2,1]$ . Det är positivt om antalet kanter inom grupper överstiger det antal som förväntas på grund av slumpen. För en given uppdelning av nätverkets hörn i vissa moduler, reflekterar modularitet koncentrationen av kanter inom moduler jämfört med slumpmässig fördelning av länkar mellan alla noder oavsett moduler.

Det finns olika metoder för att beräkna modularitet. I den vanligaste versionen av konceptet görs randomiseringen av kanterna för att bevara graden av varje vertex. Betrakta en graf med $n$ noder och $m$ länkar ( edges ) så att grafen kan delas upp i två gemenskaper med hjälp av en medlemskapsvariabel $s$ . Om en nod $v$ tillhör gemenskap 1, $s_{v}=1$ , eller om $v$ tillhör gemenskap 2, $s_{v}=-1$ . Låt närliggande matris för nätverket representeras av $A$ , där $A_{vw}=0$ betyder att det inte finns någon kant (ingen interaktion) mellan noderna $v$ och $w$ och $A_{vw}=1$ betyder att det finns en kant mellan de två. Även för enkelhetens skull betraktar vi ett oriktat nätverk. Alltså $A_{vw}=A_{wv}$ . (Det är viktigt att notera att flera kanter kan finnas mellan två noder, men här bedömer vi det enklaste fallet).

Modularitet $Q$ definieras då som bråkdelen av kanter som faller inom grupp 1 eller 2, minus det förväntade antalet kanter inom grupp 1 och 2 för en slumpmässig graf med samma nodgradsfördelning som det givna nätverket.

Det förväntade antalet flanker ska beräknas med hjälp av konceptet med en konfigurationsmodell . Konfigurationsmodellen är en randomiserad realisering av ett visst nätverk. Givet ett nätverk med $n$ noder, där varje nod $v$ har en nodgrad $k_{v}$ , skär konfigurationsmodellen varje kant i två halvor, och sedan varje halva edge, som kallas en stubb , kopplas om slumpmässigt med vilken annan stubb som helst i nätverket, vilket till och med tillåter självslingor (som uppstår när en stubb kopplas om till en annan stub från samma nod) och flera kanter mellan samma två noder. Således, även om nodgradsfördelningen av grafen förblir intakt, resulterar konfigurationsmodellen i ett helt slumpmässigt nätverk.

Förväntat antal kanter mellan noder

Betrakta nu två noder $v$ och $w$ , med nodgrader $k_{v}$ respektive $k_{w}$ från ett slumpmässigt kopplat nätverk som beskrivs ovan. Vi beräknar det förväntade antalet helkanter mellan dessa noder.

Låt oss betrakta var och en av $k_{v}$ stubbarna i nod $v$ och skapa associerade indikatorvariabler $\displaystyle I_{i}^{(v,w )}}$ för dem, $i=1,\ldots ,k_{v}$ , med $I_{i}^{( v,w)}=1$ om $i$ -th-stubben råkar ansluta till en av ${\displaystyle k_{w}}-$ stubbarna i nod $w$ i denna speciella slumpmässiga graf . Om det inte gör det, då $I_{i}^{(v,w)}=0$ . Eftersom $i$ -th stubben av nod $v$ kan ansluta till vilken som helst av de $2m-1$ återstående stubbarna med lika sannolikhet, och eftersom det finns ${\ displaystyle k_{w}}$ stubbar som den kan ansluta till associerad med nod $w$ , uppenbarligen

$p(I_{i}^{(v,w)}=1) =E[I_{i}^{(v,w)}]={\frac {k_{w}}{2m-1}}$

Det totala antalet helkanter $J_{vw}$ mellan $v$ och $w$ är bara ${\displaystyle J_{vw}=\sum _{i=1}^{k_{v}}I_{i}^{(v,w)}} , så det förväntade värdet av$ denna kvantitet är

$E[J_{vw}]=E\left[\summa _{i=1}^{k_{v}}I_{i}^{(v ,w)}\right]=\summa _{i=1}^{k_{v}}E[I_{i}^{(v,w)}]=\summa _{i=1}^{k_ {v}}{\frac {k_{w}}{2m-1}}={\frac {k_{v}k_{w}}{2m-1}}$

Många texter gör sedan följande approximationer, för slumpmässiga nätverk med ett stort antal kanter. När $m$ är stor släpper de subtraktionen av $1$ i nämnaren ovan och använder helt enkelt det ungefärliga uttrycket ${\frac {k_{v}k_{ w}}{2m}}$ för det förväntade antalet kanter mellan två noder. Dessutom, i ett stort slumpmässigt nätverk, är antalet självslingor och multi-kanter försvinnande litet. Genom att ignorera självslingor och multi-kanter kan man anta att det finns högst en kant mellan två valfria noder. I så fall $J_{vw}$ en binär indikatorvariabel, så dess förväntade värde är också sannolikheten att den är lika med $1$ , vilket betyder att man kan approximera sannolikheten för att en kant existerar mellan noder $v$ och $w$ som ${\frac {k_{v}k_{w}}{2m}}$ .

Modularitet

Därför är skillnaden mellan det faktiska antalet kanter mellan nod $v$ och $w$ och det förväntade antalet kanter mellan dem

$A_{vw}-{\frac {k_{v}k_{w}}{2m}}$

Att summera över alla nodpar ger ekvationen för modularitet, $Q$ .

$Q={\frac {1}{2m}}\sum _{vw}\left [A_{vw}-{\frac {k_{v}k_{w}}{2m}}\right]{\frac {s_{v}s_{w}+1}{2}}$

 

 

 

 

()

Det är viktigt att notera att ekv. 3 fungerar endast för uppdelning i två grupper. Hierarkisk partitionering (dvs. partitionering i två gemenskaper, sedan de två undergemenskaperna ytterligare partitionerade i två mindre undergemenskaper endast för att maximera Q ) är en möjlig metod för att identifiera flera gemenskaper i ett nätverk. Dessutom kan (3) generaliseras för att dela upp ett nätverk i c -gemenskaper.

$Q={\frac {1}{(2m)}}\summa _{vw}\left[A_{vw}-{\frac {k_{v}k_{w}}{(2m)}}\right] \delta (c_{v},c_{w})=\summa _{i=1}^{c}(e_{ii}-a_{i}^{2})$

 

 

 

 

()

där e _ij är bråkdelen av kanter med ena ändpunkten i gemenskap i och den andra i gemenskap j :

$e_{ij}=\summa _{vw}{\frac {A_{vw}}{2m}}1_ {v\in c_{i}}1_{w\in c_{j}}$

och a _i är bråkdelen av ändar av kanter som är fästa vid hörn i community i :

$a_{i}={\frac {k_{i}}{2m}}=\summa _{j}e_{ij}$

Exempel på upptäckt av flera gemenskaper

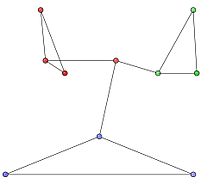
Vi betraktar ett oriktat nätverk med 10 noder och 12 kanter och följande närliggande matris.

Fig 1. Provnätverk motsvarande Adjacency-matrisen med 10 noder, 12 kanter.

Fig 2. Nätverkspartitioner som maximerar Q. Maximalt Q=0,4896

Nod-ID	1	2	3	4	5	6	7	8	9	10
1	0	1	1	0	0	0	0	0	0	1
2	1	0	1	0	0	0	0	0	0	0
3	1	1	0	0	0	0	0	0	0	0
4	0	0	0	0	1	1	0	0	0	1
5	0	0	0	1	0	1	0	0	0	0
6	0	0	0	1	1	0	0	0	0	0
7	0	0	0	0	0	0	0	1	1	1
8	0	0	0	0	0	0	1	0	1	0
9	0	0	0	0	0	0	1	1	0	0
10	1	0	0	1	0	0	1	0	0	0

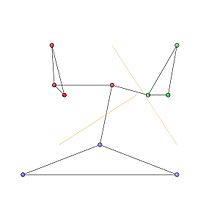
Gemenskaperna i grafen representeras av de röda, gröna och blå nodklustren i fig 1. De optimala gemenskapspartitionerna visas i fig 2.

Matrisformulering

En alternativ formulering av modulariteten, användbar speciellt i spektrala optimeringsalgoritmer, är följande. Definiera $S_{vr}$ till $1$ om vertex $v$ tillhör gruppen $r$ och $0$ annars. Sedan

$\delta (c_{v},c_{w})=\summa _{r}S_{vr}S_{wr}$

och följaktligen

$Q={\frac { 1}{2m}}\summa _{vw}\summa _{r}\left[A_{vw}-{\frac {k_{v}k_{w}}{2m}}\right]S_{vr} S_{wr}={\frac {1}{2m}}\mathrm {Tr} (\mathbf {S} ^{\mathrm {T} }\mathbf {BS} ),$

där $S$ är den (icke-kvadratiska) matrisen med elementen $S_{v}$ och $B$ är den så kallade modularitetsmatrisen, som har element

$B_{vw}=A_{vw}-{\frac {k_{v}k_{w}}{2m}}.$

Alla rader och kolumner i modularitetsmatrisen summeras till noll, vilket innebär att modulariteten för ett odelat nätverk också alltid är {\ $displaystyle 0}$ .

För nätverk uppdelade i bara två gemenskaper kan man alternativt definiera $s_{v}=\pm 1$ för att ange den gemenskap som noden $v$ tillhör, vilket sedan leder till

$over 4m}\summa _{vw}B_{vw}s_{v}s_ {w}={1 \över 4m}\mathbf {s} ^{\mathrm {T} }\mathbf {Bs} ,}$

där $s$ är kolumnvektorn med elementen $s_{v}$ .

Denna funktion har samma form som Hamiltonian för ett Ising- spinglas , en anslutning som har utnyttjats för att skapa enkla datoralgoritmer, till exempel genom att använda simulerad glödgning , för att maximera modulariteten. Den allmänna formen av modulariteten för godtyckliga antal gemenskaper är likvärdig med ett Potts spinglas och liknande algoritmer kan också utvecklas för detta fall.

Upplösningsgräns

Modularitet jämför antalet kanter inuti ett kluster med det förväntade antalet kanter som man skulle hitta i klustret om nätverket var ett slumpmässigt nätverk med samma antal noder och där varje nod behåller sin grad, men kanter är annars slumpmässigt fästa. Denna slumpmässiga nollmodell antar implicit att varje nod kan kopplas till vilken annan nod som helst i nätverket. Detta antagande är dock orimligt om nätverket är mycket stort, eftersom horisonten för en nod inkluderar en liten del av nätverket och ignorerar det mesta. Dessutom innebär detta att det förväntade antalet flanker mellan två grupper av noder minskar om storleken på nätverket ökar. Så om ett nätverk är tillräckligt stort kan det förväntade antalet flanker mellan två grupper av noder i modularitetens nollmodell vara mindre än en. Om detta händer skulle en enda kant mellan de två klustren tolkas av modularitet som ett tecken på en stark korrelation mellan de två klustren, och optimering av modularitet skulle leda till sammanslagning av de två klustren, oberoende av klustrens egenskaper. Så även svagt sammankopplade kompletta grafer, som har högsta möjliga täthet av interna kanter, och representerar de bästa identifierbara gemenskaperna, skulle slås samman genom modularitetsoptimering om nätverket var tillräckligt stort. Av denna anledning skulle optimering av modularitet i stora nätverk misslyckas med att lösa små samhällen, även när de är väldefinierade. Denna fördom är oundviklig för metoder som modularitetsoptimering, som förlitar sig på en global nollmodell.

Flerupplösningsmetoder

Det finns två huvudsakliga tillvägagångssätt som försöker lösa upplösningsgränsen inom modularitetskontexten: tillägget av ett motstånd r till varje nod, i form av en självslinga , som ökar ( r>0 ) eller minskar ( r<0 ) motvilja mot noder för att bilda gemenskaper; eller tillägget av en parameter γ>0 framför null-case-termen i definitionen av modularitet, som styr den relativa betydelsen mellan interna länkar i gemenskaperna och nollmodellen. Genom att optimera modularitet för värden på dessa parametrar i deras respektive lämpliga intervall, är det möjligt att återställa hela mesoskalan av nätverket, från makroskalan där alla noder tillhör samma gemenskap, till mikroskalan där varje nod bildar sin egen gemenskap, därav namnet multiresolution methods . Det har dock visat sig att dessa metoder har begränsningar när samhällen är mycket heterogena i storlek.

Mjukvaruverktyg

Det finns ett par mjukvaruverktyg tillgängliga som kan beräkna klustringar i grafer med god modularitet.

Ursprunglig implementering av Louvain-metoden på flera nivåer.

Leiden-algoritmen som dessutom undviker oanslutna samhällen.

Algoritmen Vienna Graph Clustering (VieClus), en parallell memetisk algoritm.

Se även

• Komplext nätverk
• Gemenskapsstruktur
• Noll modell
• Perkolationsteori