Nätverksstyrbarhet

Styr ett enkelt nätverk.

Nätverksstyrbarhet avser den strukturella styrbarheten av ett nätverk . Styrbarhet beskriver vår förmåga att styra ett dynamiskt system från vilket initialt tillstånd som helst till vilket önskat slutligt tillstånd som helst på ändlig tid, med ett lämpligt val av ingångar. Denna definition stämmer väl överens med vår intuitiva uppfattning om kontroll. Kontrollerbarheten av allmänt riktade och viktade komplexa nätverk har nyligen varit föremål för intensiva studier av ett antal grupper i många olika nätverk, världen över. Nyligen genomförda studier av Sharma et al. på biologiska nätverk av flera typer (gen-gen, miRNA-gen och protein-protein-interaktionsnätverk) identifierade kontrollmål i fenotypiskt karakteriserat osteosarkom som visar viktig roll för gener och proteiner som är ansvariga för att upprätthålla tumörmikromiljön.

Bakgrund

Betrakta den kanoniska linjära tidsinvarianta dynamiken på ett komplext nätverk ${\displaystyle {\dot {\mathbf {X} }}(t)=\ mathbf {A} \cdot \mathbf {X} (t)+\mathbf {B} \cdot \mathbf {u} (t)} där$ vektorn ${\displaystyle \mathbf {X} (t)=(x_{1}(t),\cdots ,x_{N}(t))^{\mathrm {T} }} fångar tillståndet$ för ett system av $N$ -noder vid tiden $t$ . N $N\times N$ -matrisen $\mathbf {A}$ systemets kopplingsschema och interaktionsstyrkan mellan komponenterna. N $N\times M$ -matrisen $\displaystyle \mathbf {B} }$ identifierar noderna som styrs av en extern styrenhet. Systemet styrs genom den tidsberoende ingångsvektorn $\mathbf {u} (t)=(u_{1}(t) ),\cdots ,u_{M}(t))^{\mathrm {T} }$ som styrenheten ålägger systemet. För att identifiera det minsta antalet förarnoder, betecknade med ${\displaystyle N_{\mathrm {D} }} ,$ vars kontroll är tillräcklig för att fullständigt kontrollera systemets dynamik, Liu et al. försökte kombinera verktygen från strukturkontrollteori, grafteori och statistisk fysik. De visade att det minsta antalet ingångar eller förarnoder som behövs för att upprätthålla full kontroll över nätverket bestäms av den maximala kardinalitetsmatchningen i nätverket. Från detta resultat utvecklades ett analytiskt ramverk, baserat på in-ut gradfördelningen, för att förutsäga $n_{\mathrm {D} }=N_{\mathrm {D} }/N$ för skalfria och Erdős–Rényi slumpmässiga grafer . Men på senare tid har det visat sig att nätverksstyrbarhet (och andra metoder som endast använder struktur som uteslutande använder anslutningen av en graf, ${\displaystyle \mathbf {A} } ,$ för att förenkla den underliggande dynamiken), både underskrider och överskrider antal och vilka uppsättningar av förarnoder som bäst styr nätverksdynamiken, vilket understryker vikten av redundans (t.ex. kanalisering) och icke-linjär dynamik för att bestämma kontroll.

Det är också anmärkningsvärt att Liu's et al. formulering skulle förutsäga samma värden för ${n_{\mathrm {D} }}$ för en kedjegraf och för en svag tätt sammankopplad graf. Uppenbarligen har båda dessa grafer mycket olika gradfördelningar in och ut. Ett nyligen opublicerat arbete ifrågasätter om grad , som är ett rent lokalt mått i nätverk, fullständigt skulle beskriva styrbarhet och om även något avlägsna noder inte skulle ha någon roll i att bestämma nätverksstyrbarhet. För många nätverk med riktiga ord, nämligen näringsnät, neuronala och metabola nätverk, är oöverensstämmelsen i värden för ${n_{\mathrm {D} }}^{real}$ och ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ beräknat av Liu et al. är anmärkningsvärt. Om styrbarheten avgörs huvudsakligen av grad, varför är ${n_{\mathrm {D} }}^{real}$ och ${\ displaystyle {n_{\mathrm {D} }}^{\mathrm {rand\_degree} }}$ så olika för många verkliga nätverk? De hävdade (arXiv:1203.5161v1) att detta kan bero på effekten av gradkorrelationer. Det har dock visat sig att nätverksstyrbarhet endast kan ändras genom att använda mellanhetscentralitet och närhetscentralitet , utan att använda grad (grafteori) eller gradkorrelationer alls.

Ett schematiskt diagram visar styrningen av ett riktat nätverk. För ett givet riktat nätverk (fig. a) beräknar man dess maximala matchning: en största uppsättning kanter utan gemensamma huvuden eller svansar. Den maximala matchningen kommer att bestå av en uppsättning av hörn-disjunkta riktade banor och riktade cykler (se röda kanter i Fig.b). Om en nod är ett huvud av en matchande kant, så matchas denna nod (gröna noder i fig.b). Annars är den oöverträffad (vita noder i fig.b). Dessa oöverträffade noder är de noder man behöver kontrollera, dvs förarnoderna. Genom att injicera signaler till dessa förarnoder får man en uppsättning riktad väg med startpunkter som ingångarna (se fig.c). Dessa vägar kallas "stammar". Den resulterande digrafen kallas U-rotad faktoriell anslutning. Genom att "ympa" de riktade cyklerna till dessa "stammar" får man "knoppar". Den resulterande digrafen kallas kaktusar (se fig.d). Enligt satsen för strukturell styrbarhet, eftersom det finns en kaktusstruktur som spänner över det kontrollerade nätverket (se fig. e), är systemet styrbart. Kaktusstrukturen (Fig.d) som ligger bakom det kontrollerade nätverket (Fig.e) är "skelettet" för att upprätthålla kontrollerbarhet.

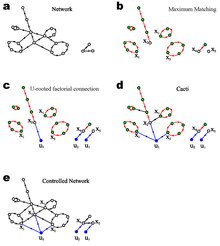
Strukturell styrbarhet

Konceptet med de strukturella egenskaperna introducerades först av Lin (1974) och utökades sedan av Shields och Pearson (1976) och alternativt härleddes av Glover och Silverman (1976). Huvudfrågan är om bristen på kontrollerbarhet eller observerbarhet är generisk med avseende på de variabla systemparametrarna. Inom ramen för strukturell styrning är systemparametrarna antingen oberoende fria variabler eller fasta nollor. Detta är konsekvent för modeller av fysiska system eftersom parametervärden aldrig är kända exakt, med undantag för nollvärden som uttrycker frånvaron av interaktioner eller kopplingar.

Maximal matchning

I grafteorin är en matchning en uppsättning kanter utan gemensamma hörn. Liu et al. utvidgade denna definition till riktad graf, där en matchning är en uppsättning riktade kanter som inte delar start- eller sluthörn. Det är lätt att kontrollera att en matchning av en riktad graf består av en uppsättning enkla banor och cykler som inte är sammankopplade med hörn. Den maximala matchningen av ett riktat nätverk kan effektivt beräknas genom att arbeta i den tvådelade representationen med den klassiska Hopcroft–Karp-algoritmen , som körs i O( E √ N ) tid i värsta fall. För oriktade grafer har analytiska lösningar av storleken och antalet maximala matchningar studerats med hjälp av kavitetsmetoden utvecklad inom statistisk fysik. Liu et al. utökade beräkningarna för riktad graf.

Genom att beräkna den maximala matchningen av ett brett utbud av verkliga nätverk, Liu et al. hävdade att antalet förarnoder huvudsakligen bestäms av nätverkets gradfördelning $P(k_{\mathrm {in} },k_{\mathrm {out} })$ . De beräknade också det genomsnittliga antalet förarnoder för en nätverksensemble med godtycklig gradfördelning med hjälp av kavitetsmetoden . Det är intressant att för en kedjegraf och en svag tätt sammankopplad graf, som båda har mycket olika gradfördelningar in och ut; formuleringen av Liu et al. skulle förutsäga samma värden för ${n_{\mathrm {D} }}$ . För många nätverk med riktiga ord, nämligen näringsnät, neuronala och metabola nätverk, är oöverensstämmelsen i värden för ${n_{\mathrm {D} }}^{real}$ och ${n_{\mathrm {D} }}^{\mathrm {rand\_degree} }$ beräknat av Liu et al. är anmärkningsvärt. Om kontrollerbarhet avgörs rent av grad, varför är ${n_{\mathrm {D} }}^{real}$ och $\ displaystyle {n_{\mathrm {D} }}^{\mathrm {rand\_degree} }}$ så olika för många verkliga nätverk? Det är fortfarande öppet för granskning om "kontrollrobusthet" i nätverk påverkas mer genom att använda mellanhetscentralitet och närhetscentralitet över gradbaserade mått.

Även om glesare grafer är svårare att kontrollera, skulle det uppenbarligen vara intressant att ta reda på om mellanhetscentralitet och närhetscentralitet eller gradheterogenitet spelar en viktigare roll för att avgöra kontrollerbarheten av glesa grafer med nästan liknande gradfördelningar.

Kontroll av sammansatta kvantsystem och algebraisk grafteori

En styrteori om nätverk har också utvecklats inom ramen för universell styrning för sammansatta kvantsystem, där subsystem och deras interaktioner är associerade med noder respektive länkar. Detta ramverk tillåter formulering av Kalmans kriterium med verktyg från algebraisk grafteori via minimirankningen av en graf och relaterade begrepp.

Se även

• Styrbarhet Gramian

externa länkar

• Webbplatsen för nätverksstyrbarhetsprojektet
• Videon som visar nätverksstyrbarhet