Examensfördelning

I studiet av grafer och nätverk är graden av en nod i ett nätverk antalet anslutningar den har till andra noder och gradfördelningen är sannolikhetsfördelningen av dessa grader över hela nätverket.

Definition

Graden av en nod i ett nätverk (ibland hänvisad till felaktigt som anslutningen ) är antalet anslutningar eller kanter som noden har till andra noder . Om ett nätverk är riktat , vilket betyder att kanter pekar i en riktning från en nod till en annan nod, så har noderna två olika grader, in-graden, som är antalet inkommande kanter, och ut-graden, som är antalet av utgående kanter.

Gradfördelningen P ( k ) för ett nätverk definieras sedan till att vara andelen noder i nätverket med grad k . Om det alltså finns n noder totalt i ett nätverk och n _k av dem har graden k , har vi $P(k)={\frac {n_{k}}{n} }$ .

Samma information presenteras också ibland i form av en kumulativ gradfördelning , andelen noder med grad mindre än k , eller till och med den komplementära kumulativa gradfördelningen, andelen noder med grad större än eller lika med k (1- C ) ) om man betraktar C som den kumulativa gradfördelningen ; dvs komplementet till C .

Observerade gradfördelningar

Examensfördelningen är mycket viktig för att studera både verkliga nätverk, såsom Internet och sociala nätverk , och teoretiska nätverk. Den enklaste nätverksmodellen, till exempel, (Erdős–Rényi-modellen) slumpmässiga grafen , där var och en av n noder är oberoende ansluten (eller inte) med sannolikheten p (eller 1 − p ), har en binomialfördelning av grader k :

P(k)={n-1 \choose k}p^{k}(1-p) ^{n-1-k},

(eller Poisson i gränsen för stort n , om medelgraden $\langle k\rangle =p(n-1)$ hålls fast). De flesta nätverk i den verkliga världen har dock gradfördelningar som skiljer sig mycket från detta. De flesta är mycket höger-skeva , vilket betyder att en stor majoritet av noder har låg grad men ett litet antal, känt som "hubbar", har hög grad. Vissa nätverk, särskilt Internet, World Wide Web och vissa sociala nätverk hävdades ha gradfördelningar som ungefär följer en maktlag : $P(k)\sim k^{- \gamma }$ , där γ är en konstant. Sådana nätverk kallas skalfria nätverk och har rönt särskild uppmärksamhet för sina strukturella och dynamiska egenskaper. En undersökning av ett brett utbud av verkliga nätverk tyder dock på att skalfria nätverk är sällsynta när de bedöms med statistiskt rigorösa mått. Vissa forskare har ifrågasatt dessa fynd och hävdat att definitionerna som används i studien är olämpligt strikta, medan andra har hävdat att den exakta funktionella formen av gradfördelningen är mindre viktig än att veta om gradfördelningen är fettsvansad eller inte . Övertolkningen av specifika former av examensfördelningen har också kritiserats för att inte ta hänsyn till hur nätverk kan utvecklas över tid.

Överskjutande gradfördelning

Excess graddistribution är sannolikhetsfördelningen, för en nod som nås genom att följa en kant, av antalet andra kanter kopplade till den noden. Med andra ord är det fördelningen av utgående länkar från en nod som nås genom att följa en länk.

Antag att ett nätverk har en gradfördelning $P(k)$ , genom att välja en nod (slumpmässigt eller inte) och gå till en av dess grannar (förutsatt att det åtminstone har en granne), då är sannolikheten för att noden ska ha $k$ grannar ges inte av $P(k)$ . Anledningen är att närhelst någon nod väljs i ett heterogent nätverk är det mer sannolikt att nå naven genom att följa en av de befintliga grannarna till den noden. Den sanna sannolikheten för att sådana noder ska ha graden $k$ är $q(k)$ som kallas överskottsgraden för den noden. I konfigurationsmodellen , vilka korrelationer mellan noderna har ignorerats och varje nod antas vara ansluten till andra noder i nätverket med samma sannolikhet, kan överskottsgradsfördelningen hittas som:

$q(k)={\frac {k+1}{\langle k\rangle }}P(k+1),$

där ${\langle k\rangle }$ är medelgraden (genomsnittlig grad) för modellen. Det följer av detta faktum att medelgraden för någon nods granne är större än medelgraden för den noden. I sociala nätverk betyder det att dina vänner i genomsnitt har fler vänner än du. Detta är känt som vänskapsparadoxen . Det kan visas att ett nätverk kan ha en gigantisk komponent , om dess genomsnittliga överskottsgrad är större än en:

$\sum _{k}kq(k)>1\höger {\langle k^{2}\rangle }/{\langle k\rangle }-1>1\Rightarrow {\langle k^{2}\rangle }-2{\langle k\rangle }>0$

Tänk på att de två sista ekvationerna bara är för konfigurationsmodellen och för att härleda överskottsgradsfördelningen av ett verkligt ordnätverk bör vi också lägga till gradkorrelationer i beaktande.

Metoden för att generera funktioner

Genereringsfunktioner kan användas för att beräkna olika egenskaper hos slumpmässiga nätverk. Givet gradfördelningen och överskottsgradsfördelningen för något nätverk, $P(k)$ respektive $q(k)$ , är det möjligt att skriva två potensserier i följande formulär:

$G_{0}(x)=\textstyle \sum _{k}\displaystyle P(k)x^{k}$ och $G_{1}(x)=\textstyle \sum _{k}\displaystyle q(k)x ^{k}=\textstil \sum _{k}\displaystyle {\frac {k}{\langle k\rangle }}P(k)x^{k-1}$

$G_{1}(x)$ kan också erhållas från derivator av $G_{0}(x)$ :

$G_{1}(x)={\frac {G'_{0}(x)}{G'_{0}(1 )}}$

Om vi känner till genereringsfunktionen för en sannolikhetsfördelning $P(k)$ så kan vi återställa värdena för $P(k)$ genom att differentiera:

$P(k)={\frac {1}{k!}}{\operatörsnamn {d} ^{k}\!G \över \operatörsnamn {d} \!x^{k}}{ \biggl \vert }_{x=0}$

Vissa egenskaper, t.ex. momenten, kan enkelt beräknas från $G_{0}(x)$ och dess derivator:

${\langle k\rangle }=G'_{0}(1)$
${\langle k^{2}\rangle }=G''_{0}(1)+G'_{0}(1 )$

Och i allmänhet:

${\langle k^{m}\rangle }={\Biggl [}{{\bigg (}\operatörsnamn { x} {\operatörsnamn {d} \! \over \operatörsnamn {dx} \!}{\biggl )}^{m}}G_{0}(x){\Biggl ]}_{x=1}$

För Poisson -distribuerade slumpmässiga nätverk, såsom ER-grafen , ${\displaystyle G_{1}(x)=G_{0}(x)} ,$ är det anledningen till att teorin av slumpmässiga nätverk av denna typ är särskilt enkelt. Sannolikhetsfördelningarna för 1:a och 2:a närmaste grannar genereras av funktionerna $G_{0}(x)$ och $G_{0}(G_{ 1}(x))$ . I förlängningen genereras fördelningen av ${\displaystyle m} -th grannar av:$

$G_{0}{\bigl (}G_{1}(...G_{1}(x)...){ \bigr )}$ , med $m-1$ iterationer av funktionen $G_{1}$ som verkar på sig själv.

Det genomsnittliga antalet 1:a grannar, $c_{1}$ , är ${\displaystyle {\langle k\rangle }={dG_{0}(x) \over dx}|_{x=1}} och det genomsnittliga$ antalet 2:a grannar är: $c_ {2}={\biggl [}{d \over dx}G_{0}{\big (}G_{1}(x){\big )}{\biggl ]}_{x=1}=G_{ 1}'(1)G'_{0}{\big (}G_{1}(1){\big )}=G_{1}'(1)G'_{0}(1)=G' '_{0}(1)$

Examensfördelning för riktade nätverk

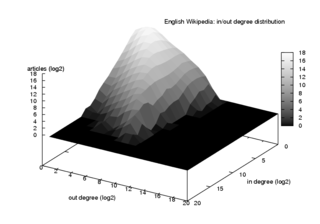
In/ut gradfördelning för Wikipedias hyperlänksgraf (logaritmiska skalor)

I ett riktat nätverk har varje nod några in-grad $k_{in}$ och några out-degree $k_{out}$ som är antalet länkar som har körts in i och ut ur den noden respektfullt. Om $P(k_{in},k_{out})$ är sannolikheten att en slumpmässigt vald nod har in-grad $k_{in}$ och utgradera $k_{out}$ så kan den genererande funktionen som är tilldelad denna gemensamma sannolikhetsfördelning skrivas med två värdesaker $x$ och $y$ som:

${\mathcal {G}}(x,y)=\summa _{k_{in},k_{out}}\displaystyle P({k_{in},k_{out}})x^{k_ {in}}y^{k_{out}}.$

Eftersom varje länk i ett riktat nätverk måste lämna någon nod och gå in i en annan, är det genomsnittliga nettoantalet länkar som går in i en nod noll. Därför,

$\langle {k_{ in}-k_{ut}}\rangle =\summa _{k_{in},k_{out}}\displaystyle (k_{in}-k_{out})P({k_{in},k_{out} })=0$ ,

vilket innebär att generationsfunktionen måste uppfylla:

${\partial {\mathcal {G}} \over \partial x}\vert _{x,y=1}={\partial {\mathcal {G}} \over \partial y}\vert _{x,y=1}=c,$

där $c$ är medelgraden (både in och ut) av noderna i nätverket; $\langle {k_{in}}\rangle =\langle {k_{out}}\rangle =c.$

Genom att använda funktionen ${\mathcal {G}}(x,y)$ kan vi återigen hitta genereringsfunktionen för in/ut-gradsfördelningen och in/ut-excess gradfördelningen, som förut. $G_{0}^{in}(x)$ kan definieras som genererande funktioner för antalet ankommande länkar vid en slumpmässigt vald nod, och $G_{1}^{in}(x)$ kan definieras som antalet ankommande länkar till en nod som nås genom att följa en slumpmässigt vald länk. Vi kan också definiera genereringsfunktioner $G_{0}^{out}(y)$ och $G_{1}^{out}(y )$ för numret som lämnar en sådan nod:

$G_{0}^{in}(x)={\mathcal {G}}(x,1)$
$G_{1}^{in}(x)={\frac {1}{c}}{\partial {\mathcal {G}} \over \partial x}\vert _{y= 1}$
$G_{0}^{out}(y)={\mathcal {G}}(1,y)$
$G_{1}^{out}(y)={\frac {1}{c}}{\partial {\mathcal {G}} \over \partial y}\vert _{x= 1}$

Här är det genomsnittliga antalet 1:a grannar, $c$ , eller som tidigare introducerats som $c_{1}$ , ${\partial {\mathcal {G}} \over \partial x}{\biggl \vert }_{x,y=1}={\partial {\mathcal {G}} \ över \partial y}{\biggl \vert }_{x,y=1}$ och det genomsnittliga antalet andra grannar som kan nås från en slumpmässigt vald nod ges av: $c_{2}=G_{1}'(1)G'_{0}(1)={\partial ^{2}{\mathcal {G}} \over \partial x \partial y}{\biggl \vert }_{x,y=1}$ . Dessa är också antalet 1:a och 2:a grannar från vilka en slumpmässig nod kan nås, eftersom dessa ekvationer är uppenbart symmetriska i $x$ och $y$ .

Examensfördelning för tecknade nätverk

I ett signerat nätverk har varje nod en positiv grad $k_{+}$ och en negativ grad $k_{-}$ som är det positiva antalet länkar och det negativa antalet länkar kopplade till den noden respektfullt. Så $P(k_{+})$ och $P(k_{-})$ betecknar negativ gradfördelning och positiv gradfördelning av det signerade nätverket.

Se även

Albert, R.; Barabasi, A.-L. (2002). "Statistisk mekanik för komplexa nätverk". Recensioner av modern fysik . 74 (1): 47–97. arXiv : cond-mat/0106096 . Bibcode : 2002RvMP...74...47A . doi : 10.1103/RevModPhys.74.47 . S2CID 60545 .
Dorogovtsev, S.; Mendes, JFF (2002). "Evolution av nätverk". Framsteg inom fysik . 51 (4): 1079–1187. arXiv : cond-mat/0106144 . Bibcode : 2002AdPhy..51.1079D . doi : 10.1080/00018730110112519 . S2CID 429546 .
Newman, MEJ (2003). "Strukturen och funktionen av komplexa nätverk". SIAM recension . 45 (2): 167–256. arXiv : cond-mat/0303516 . Bibcode : 2003SIAMR..45..167N . doi : 10.1137/S003614450342480 . S2CID 221278130 .