Beroendenätverk

Beroendenätverksmetoden tillhandahåller en systemnivåanalys av aktiviteten och topologin för riktade nätverk . Tillvägagångssättet extraherar kausala topologiska relationer mellan nätverkets noder (när nätverksstrukturen analyseras), och ger ett viktigt steg mot slutledning av kausala aktivitetsrelationer mellan nätverksnoderna ( när nätverksaktiviteten analyseras). Denna metod har ursprungligen introducerats för att studera finansiella data, den har utökats och tillämpats på andra system, såsom immunsystemet och semantiska nätverk .

När det gäller nätverksaktivitet baseras analysen på partiella korrelationer , som blir allt vanligare för att undersöka komplexa system . Med enkla ord är den partiella (eller resterande) korrelationen ett mått på effekten (eller bidraget) av en given nod, säg j , på korrelationerna mellan ett annat nodpar, säg i och k . Med detta koncept beräknas beroendet av en nod av en annan nod för hela nätverket. Detta resulterar i en riktad viktad närliggande matris för ett fullt anslutet nätverk. När närliggande matris har konstruerats kan olika algoritmer användas för att konstruera nätverket, såsom ett tröskelnätverk, Minimal Spanning Tree (MST) , Planar Maximally Filtered Graph (PMFG) och andra.

Beroendenätverk av finansiell data, för 300 av S&P500-aktierna, handlades mellan 2001–2003. Aktier är grupperade efter ekonomiska sektorer och pilen pekar i riktning mot påverkan. Nätverkets nav, den sektor som har störst inflytande, är finanssektorn. Reproduktion från Kenett et al., PLoS ONE 5(12), e15032 (2010)

Betydelse

Det partiella korrelationsbaserade beroendenätverket är en klass av korrelationsnätverk som kan avslöja dolda relationer mellan dess noder.

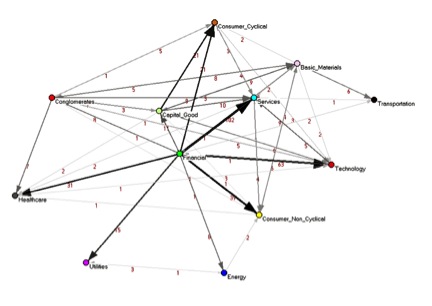
Denna ursprungliga metod presenterades först i slutet av 2010, publicerad i PLoS ONE . De avslöjade kvantitativt dold information om den underliggande strukturen på den amerikanska aktiemarknaden , information som inte fanns i standardkorrelationsnätverken . Ett av huvudresultaten av detta arbete är att under den undersökta tidsperioden (2001–2003) domineras nätverkets struktur av företag som tillhör den finansiella sektorn , som är nav i beroendenätverket. Därmed kunde de för första gången kvantitativt visa beroendeförhållandena mellan de olika ekonomiska sektorerna . Efter detta arbete har metoden för beroendenätverk tillämpats på studiet av immunsystemet och semantiska nätverk . Som sådan är denna metod tillämplig på alla komplexa system .

Beroende Nätverk av specifik antikroppsaktivitet, mätt för en grupp mödrar. Panel (a) presenterar beroendenätverket och panel (b) standardkorrelationsnätverket. Reproduktion från Madi et al., Chaos 21, 016109 (2011)

Exempel på beroendenätverk av föreningar, konstruerat från ett fullständigt semantiskt nätverk. Reproduktion från Kenett et al., PLoS ONE 6(8): e23912 (2011)

Översikt

För att vara mer specifik, de partiella korrelationerna för paret, givet j är korrelationerna mellan dem efter korrekt subtraktion av korrelationerna mellan i och j och mellan k och j . Definierat på detta sätt ger skillnaden mellan korrelationerna och de partiella korrelationerna ett mått på påverkan av nod j på korrelationen . Därför definierar vi inflytandet av nod j på nod i , eller beroendet av nod i på nod j − D ( i , j ), till summan av påverkan av nod j på korrelationerna av nod i med alla andra noder .

När det gäller nätverkstopologi baseras analysen på effekten av nodborttagning på de kortaste vägarna mellan nätverksnoderna. Mer specifikt definierar vi påverkan av nod j på varje par av noder (i,k) att vara inversen av det topologiska avståndet mellan dessa noder i närvaro av j minus det omvända avståndet mellan dem i frånvaro av nod j . Sedan definierar vi påverkan av nod j på nod i , eller beroendet av nod i på nod j − D ( i , j ), till summan av påverkan av nod j på avstånden mellan nod i med alla andra noder k .

Aktivitetsberoendenätverken

Korrelationerna mellan nod och nod

Nod-nod-korrelationerna kan beräknas med Pearsons formel :

C_{i,j}={\frac {\left\langle ( X_{i}(n)-\mu _{i})(X_{j}(n)-\mu _{j})\right\rangle }{\sigma _{i}\sigma _{j}} }

Där $X_{i}(n)$ och $X_{j}(n)$ är aktiviteten för noderna i och j i ämnet n, står μ för medelvärde och sigma STD för dynamikprofilerna för noderna i och j . Notera att nod-nodkorrelationerna (eller för enkelhetens skull nodkorrelationerna) för alla nodpar definierar en symmetrisk korrelationsmatris vars ( $\displaystyle (i,j)}$ element är korrelationen mellan noderna i och j .

Partiella korrelationer

Därefter använder vi de resulterande nodkorrelationerna för att beräkna de partiella korrelationerna. Den första ordningens partiella korrelationskoefficient är ett statistiskt mått som indikerar hur en tredje variabel påverkar korrelationen mellan två andra variabler. Den partiella korrelationen mellan noderna i och k med avseende på en tredje nod $j-PC(i,k\mid j)$ definieras som:

PC(i,k\mid j)={\frac {C(i,k)-C(i,j)C(k,j)}{\sqrt {[1-C^{2} (i,j)][1-C^{2}(k,j)]}}}

där $C(i,j),C(i,k)$ och $C(j,k)$ är nodkorrelationer definierade ovan.

Korrelationsinflytande och korrelationsberoende

Den relativa effekten av korrelationerna $C(i,j)$ och $C(j,k)$ för nod j på korrelationen C ( i , k ) ges av:

d(i,k\mid j)\equiv C(i,k)-PC(i, k|j)

Detta undviker det triviala fallet där nod j verkar starkt påverka korrelationen $C(i,k)$ , främst eftersom $C (i,j),C(i,k)$ och $C(j,k)$ har små värden. Vi noterar att denna kvantitet kan ses antingen som korrelationsberoendet av C ( i , k ) på nod j , (termen som används här) eller som korrelationsinverkan av nod j på korrelationen C ( i , k ).

Nodaktivitetsberoenden

Därefter definierar vi den totala påverkan av nod j på nod i , eller beroendet D ( i , j ) för nod i på nod j :

D(i,j)={\frac {1}{N-1}}\summa _{k\neq j}^{N-1}d(i,k\mid j)

Såsom definierat är D ( i , j ) ett mått på det genomsnittliga inflytandet av nod j på korrelationerna C(i,k) över alla noder k som inte är lika med j . Nodaktivitetsberoendena definierar en beroendematris D vars ( i , j ) element är beroendet av nod i på nod j . Det är viktigt att notera att medan korrelationsmatrisen C är en symmetrisk matris, är beroendematrisen D osymmetrisk – $D(i,j)\neq D(j) ,i)$ eftersom påverkan av nod j på nod i inte är lika med påverkan av nod i på nod j . Av denna anledning måste några av metoderna som används i analyserna av korrelationsmatrisen (t.ex. PCA) ersättas eller är mindre effektiva. Ändå finns det andra metoder, som de som används här, som korrekt kan redogöra för den icke-symmetriska karaktären hos beroendematrisen.

Strukturberoendenätverk

Vägpåverkan och avståndsberoende: Den relativa effekten av nod j på den riktade vägen $DP(i\rightarrow k|j)$ – den kortaste topologiska vägen med varje segment motsvarar en avstånd 1, mellan noderna i och k ges:

DP(i\högerpil k\mid j)\equiv {\ frac {1}{td(i\rightarrow k\mid j^{+})}}-{\frac {1}{td(i\rightarrow k\mid j^{-})}}

där $td(i\rightarrow k|j^{+})$ och $td(i\rightarrow k\mid j^{-})$ är den kortaste riktade topologiska vägen från nod i till nod k i närvaro respektive frånvaro av nod j .

Nodstrukturella beroenden

Därefter definierar vi den totala påverkan av nod j på nod i , eller beroendet D ( i , j ) för nod i på nod j :

$D(i,j)={\frac {1}{N-1}}\ summa _{k=1}^{N-1}DP(i\högerpil k\mid j)$

Såsom definierat är D ( i , j ) ett mått på det genomsnittliga inflytandet av nod j på de riktade vägarna från nod i till alla andra noder k . Nodens strukturella beroenden definierar en beroendematris D vars ( i , j ) element är beroendet av nod i på nod j , eller påverkan av nod j på nod i . Det är viktigt att notera att beroendematrisen D är osymmetrisk – $D(i,j)\neq D(j,i)$ sedan påverkan av nod j på nod i är inte lika med påverkan av nod i på nod j .

Visualisering av beroendenätverket

Beroendematrisen är den viktade närliggande matrisen, som representerar det helt anslutna nätverket. Olika algoritmer kan användas för att filtrera det helt anslutna nätverket för att erhålla den mest meningsfulla informationen, till exempel att använda ett tröskelvärde eller olika beskärningsalgoritmer. En allmänt använd metod för att konstruera informativ subgraf över ett komplett nätverk är Minimum Spanning Tree (MST). En annan informativ subgraf, som behåller mer information (i jämförelse med MST) är Planar Maximally Filtered Graph (PMFG) som används här. Båda metoderna är baserade på hierarkisk klustring och de resulterande subgraferna inkluderar alla de N noder i nätverket vars kanter representerar de mest relevanta associationskorrelationerna. MST-undergrafen innehåller $(N-1)$ kanter utan loopar medan PMFG-undergrafen innehåller $3(N-2)$ kanter.

Se även

externa länkar