Goldberg–Coxeter konstruktion

Goldberg polyeder (3,1) och geodetisk polyeder (3,1). Goldberg-polyedrarna och geodetiska polyedrarna var föregångare till Goldberg-Coxeter-operationen.

Goldberg -Coxeter-konstruktionen eller Goldberg-Coxeter-operationen ( GC-konstruktion eller GC-operation ) är en grafoperation definierad på vanliga polyedriska grafer med grad 3 eller 4. Det gäller även den dubbla grafen för dessa grafer, dvs grafer med triangulära eller fyrsidiga " ansikten". GC-konstruktionen kan ses som att dela upp ytorna på en polyeder med ett gitter av triangulära, fyrkantiga eller hexagonala polygoner, möjligen snedställda i förhållande till den ursprungliga ytan: det är en förlängning av begrepp som introducerats av Goldberg-polyedrarna och geodetiska polyedrar . GC-konstruktionen studeras främst inom organisk kemi för dess tillämpning på fullerener , men den har tillämpats på nanopartiklar , datorstödd design , korgvävning och den allmänna studien av grafteori och polyedrar .

Goldberg-Coxeter-konstruktionen kan betecknas som ${\displaystyle GC_{k,\ell }(G_{0})} ,$ där $G_{0}$ är grafen som används on, $k$ och $l$ är heltal, $k>0$ och $\ell \geq 0$ .

Historia

Michael Goldberg introducerade Goldberg-polyedern 1937. Buckminster Fuller myntade termen " geodesisk kupol " på 1940-talet, även om han till stor del höll matematiken bakom kupolerna en affärshemlighet. Geodetiska kupoler är den geometriska dualen av (en sektion av) en Goldberg-polyeder: en fullständig geodetisk kupol kan ses som en geodetisk polyeder , dubbel till Goldberg-polyedern. 1962 Donald Caspar och Aaron Klug en artikel om geometrin hos virala kapsider som tillämpade och utökade koncept från Goldberg och Fuller. HSM Coxeter publicerade en artikel 1971 som täckte mycket av samma information. Caspar och Klug var de första som publicerade den mest allmänna korrekta konstruktionen av en geodetisk polyeder, vilket gjorde namnet "Goldberg-Coxeter-konstruktion" till ett exempel på Stiglers lag om eponymi .

Upptäckten av Buckminsterfulleren 1985 motiverade forskning om andra molekyler med strukturen av en Goldberg-polyeder. Termerna "Goldberg–Coxeter fulleren" och "Goldberg–Coxeter-konstruktion" introducerades av Michel Deza år 2000. Detta är också första gången grad 4-fallet övervägdes.

Konstruktion

Detta avsnitt följer till stor del Deza et al.s två artiklar.

Mästarpolygoner

Galler
n-vanlig	3	4
Domän	Eisenstein $a+bu$	Gaussisk $a+bi$
Angränsande enhet	${\begin{aligned}u&={\frac {1}{2}}\left(1+i{\sqrt {3}}\right)\\&=e^{{\frac {1}{3}}\pi i}=\omega +1\end{aligned}}$	$i={\sqrt {-1}}$
Norm $t(a,b)$	$a^{2}+ab+b^{2}$	$a^{2}+b^{2}$ .
Master polygon	$(0,x,xu)$	$(0,x,x(1+i),xi)$

Regelbundna gitter över det komplexa planet kan användas för att skapa "masterpolygoner". I geodetisk kupolterminologi är detta "nedbrytningsstrukturen" eller "principal polyhedral triangel" (PPT). Det 4-regelbundna fallet använder det kvadratiska gittret över de Gaussiska heltal , och det 3-reguljära fallet använder triangulärt gitter över de Eisenstein-heltalen . För enkelhetens skull används en alternativ parametrisering av Eisenstein-heltalen, baserad på den sjätte roten av enhet istället för den tredje. Den vanliga definitionen av Eisenstein-heltal använder elementet ${\textstyle \omega ={\frac {1}{2}}\left(- 1+i{\sqrt {3}}\right)=e^{{\frac {2}{3}}\pi i}=u-1}$ . En norm, $t(k,\ell )$ , definieras som kvadraten på det komplexa talets absoluta värde. För 3-regelbundna grafer är denna norm T-talet eller trianguleringstalet som används inom virologi.

Huvudpolygonen är en liksidig triangel eller kvadrat som läggs över gittret. Tabellen till höger ger formler för huvudpolygonernas hörn i det komplexa planet, och galleriet nedan visar mastertriangeln och kvadraten (3,2). Så att polygonen kan beskrivas med ett enda komplext tal, är en vertex fixerad till 0. Det finns flera tal som kan beskriva samma polygon: dessa är associerade till varandra: if $x$ och $y$ är associerade, då $x=u^{n}y$ i Eisensteins eller $x=i^{n}y$ i Gausserna för något heltal $n$ . Uppsättningen av element som är associerade med varandra är en ekvivalensklass , och elementet i varje ekvivalensklass som har $a>0$ och $b\geq 0$ är normalformen .

(3,2) mastertriangel över triangulärt rutnät
(3,2) huvudruta över kvadratiskt rutnät

Masterpolygoner, och operatorn ${\displaystyle GC_{k,\ell }\left(G_{0}\right)} ,$ kan klassificeras enligt följande:

Klass I: $\ell =0.$
Klass II: $k=\ell .$
Klass III: alla andra. Klass III-operatorer finns i kirala par: $GC_{k,\ell }\left(G_{0}\right)$ är det kirala paret av $GC_{\ell ,k}(G_{0})$ .

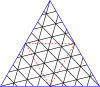
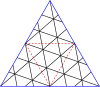
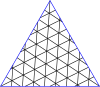
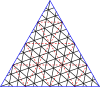
Nedan finns tabeller över mastertrianglar och fyrkanter. Klass I motsvarar den första kolumnen och klass II motsvarar diagonalen med en något mörkare bakgrund.

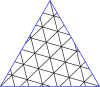
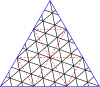
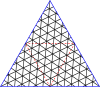
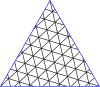
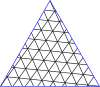
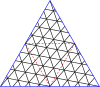
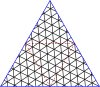
Masterpolygoner för trianglar

Bemästra trianglar till (8,8)
	0	1	2	3	4	5	6	7	8
1
2
3
4
5
6
7
8

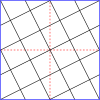
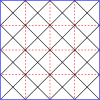
Masterpolygoner för rutor

Master rutor genom (8,8)
	0	1	2	3	4	5	6	7	8
1
2
3
4
5
6
7
8

Sammansättningen av Goldberg-Coxeter-operationer motsvarar multiplikation av komplexa tal. Om och endast om $GC_{a,b}\left(GC_{c,d}\left(G_) {0}\right)\right)=GC_{e,f}\left(G_{0}\right)$ (dvs serien av operationer till vänster ger en graf som är isomorf till den till höger), sedan för en 3-regelbunden graf $(a+bu)(c+du)$ är i ekvivalensklassen för $(e+fu) )$ , och för en 4-regelbunden graf $(a+bi)(c+di)$ i ekvivalensklassen för ${\ displaystyle (e+fi)}$ . Det finns några användbara konsekvenser av detta:

Tillämpningen av upprepade Goldberg-Coxeter-operationer är kommutativ och associativ .
Komplex konjugering av elementet $a+bi$ eller $a+bu$ motsvarar reflektion av den konstruerade grafen.
Eftersom de Gaussiska heltal och euklidiska heltal båda är euklidiska domäner , kan element av dessa domäner unikt inkluderas i prime element. Därför är det också vettigt att dekomponera en Goldberg-Coxeter-operator till en sekvens av "primära" Goldberg-Coxeter-operatorer, och denna sekvens är unik (upp till omarrangemang).

Utför GC-konstruktionen

Stegen för att utföra GC-konstruktionen $GC_{k,\ell }(G_{0})$ är som följer:

Bestäm huvudpolygonen, baserat på $k$ , $\ell$ och $G_{0}$
Om du använder en 3- eller 4-regelbunden graf (istället för en graf med triangulära/fyrsidiga ytor), ta dess dubbla graf . Denna dubbla graf kommer att ha triangulära eller fyrsidiga ytor.
Byt ut ytorna på den triangulerade/kvadrangulerade grafen med huvudpolygonen. Var medveten om att plana grafer har en "extern" yta som också måste bytas ut. I exemplet nedan görs detta genom att fästa det på ena sidan av grafen och ansluta andra sidor vid behov. Detta introducerar tillfälligt överlappande kanter i grafen, men den resulterande grafen är plan. Topparna kan omarrangeras så att det inte finns några överlappande kanter.
Om den ursprungliga grafen var en 3- eller 4-regelbunden graf, ta dualen av resultatet från steg 3. Annars är resultatet av steg 3 GC-konstruktionen.

Nedan är ett exempel, där $GC_{1,1}(G_{0})$ är konstruerad på skelettet av en kub . I de två sista graferna är blå linjer kanterna på $G_{0}$ , medan svarta linjer är kanterna på $GC_{1,1}(G_{0})$ . (Prickade linjer är normala grafkanter, bara ritade annorlunda för att göra överlappande grafkanter mer synliga.) Röda hörn är i $G_{0}$ och förblir i $GC_{1 ,1}(G_{0})$ , medan blå hörn är nyskapade av konstruktionen och endast finns i $GC_{1,1}(G_{0})$ .

Master square (1,1)
Startpolyeder (kub)
$G_{0}$ , kubens skelett
Mellansteg för att konstruera $GC_{1,1}(G_{0})$ .
Resultatet $GC_{1,1}(G_{0})$ , efter omarrangemang
Inbäddning av resultatet ( rhombic dodecahedron )

Tillägg

Goldberg-Coxeter-konstruktionen kan enkelt utökas till vissa icke-plana grafer, som toroidformade grafer . Klass III-operatorer kräver på grund av sin kiralitet en graf som kan bäddas in på en orienterbar yta , men klass I- och II-operatorer kan användas på icke-orienterbara grafer.

Se även

Fotnoter