Franck-Condon-principen

Figur 1. Franck–Condon princip energidiagram. Eftersom elektroniska övergångar är mycket snabba jämfört med nukleära rörelser, är vibrationstillstånden till och från vilka absorption och emission sker de som motsvarar en minimal förändring av kärnkoordinaterna. Som ett resultat producerar både absorption och emission molekyler i vibrationellt exciterade tillstånd . De potentiella brunnarna visas gynna övergångar med förändringar i ν .

Franck –Condon-principen (uppkallad efter James Franck och Edward Condon ) är en regel inom spektroskopi och kvantkemi som förklarar intensiteten av vibroniska övergångar (de samtidiga förändringar i elektroniska och vibrationsenerginivåer hos en molekyl på grund av absorption eller emission av en foton av lämplig energi). Principen säger att under en elektronisk övergång kommer en förändring från en vibrationsenerginivå till en annan att vara mer sannolikt att inträffa om de två vibrationsvågfunktionerna överlappar mer signifikant.

Översikt

Figur 2. Schematisk representation av absorptions- och fluorescensspektra som motsvarar energidiagrammet i figur 1. Symmetrin beror på den lika formen av jord- och exciterade potentialbrunnar. De smala linjerna kan vanligtvis endast observeras i spektra av utspädda gaser. De mörkare kurvorna representerar den inhomogena breddningen av samma övergångar som sker i vätskor och fasta ämnen. Elektroniska övergångar mellan de lägsta vibrationsnivåerna i de elektroniska tillstånden (0–0-övergången) har samma energi i både absorption och fluorescens.

Figur 3. Semiklassisk pendelanalogi av Franck-Condon-principen. Vibrationsövergångar är tillåtna vid de klassiska vändpunkterna eftersom både rörelsemängden och kärnkoordinaterna motsvarar de två representerade energinivåerna. I denna illustration är vibrationsövergångarna 0–2 gynnade.

Franck-Condon-principen har en väletablerad semiklassisk tolkning baserad på James Francks ursprungliga bidrag . Elektroniska övergångar är relativt momentana jämfört med tidsskalan för kärnrörelser, därför om molekylen ska flytta till en ny vibrationsnivå under den elektroniska övergången, måste denna nya vibrationsnivå vara omedelbart kompatibel med de nukleära positionerna och momenten för vibrationsnivån hos molekylen i ursprungligt elektroniskt tillstånd. I den semiklassiska bilden av vibrationer (oscillationer) hos en enkel harmonisk oscillator kan de nödvändiga förhållandena uppstå vid vändpunkterna, där rörelsemängden är noll.

Klassiskt är Franck-Condon-principen approximationen att en elektronisk övergång är mest sannolikt att inträffa utan förändringar i positionerna för kärnorna i den molekylära enheten och dess miljö. Det resulterande tillståndet kallas ett Franck-Condon-tillstånd, och den inblandade övergången, en vertikal övergång. Den kvantmekaniska formuleringen av denna princip är att intensiteten av en vibrationsövergång är proportionell mot kvadraten på överlappningsintegralen mellan vibrationsvågfunktionerna för de två tillstånden som är involverade i övergången.

— IUPAC Compendium of Chemical Terminology, 2:a upplagan (1997)

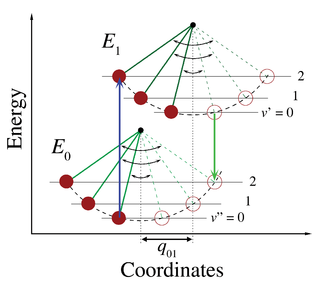
I den kvantmekaniska bilden är vibrationsnivåerna och vibrationsvågfunktionerna de för kvantharmoniska oscillatorer , eller av mer komplexa approximationer till den potentiella energin hos molekyler, såsom Morsepotentialen . Figur 1 illustrerar Franck-Condon-principen för vibroniska övergångar i en molekyl med morseliknande potentiella energifunktioner i både marken och exciterade elektroniska tillstånd. I den låga temperaturapproximationen börjar molekylen i vibrationsnivån v = 0 i det elektroniska marktillståndet och gör en övergång till det exciterade elektroniska tillståndet när den absorberar en foton med den nödvändiga energin. Elektronkonfigurationen av det nya tillståndet kan resultera i en förskjutning av jämviktspositionen för kärnorna som utgör molekylen. I figur 3 är denna förskjutning _i nukleära koordinater mellan marken och det första exciterade tillståndet märkt som q01 . I det enklaste fallet med en diatomisk molekyl hänvisar kärnkoordinataxeln till den internukleära separationen. Vibronövergången indikeras av en vertikal pil på grund av antagandet om konstanta kärnkoordinater under övergången. Sannolikheten att molekylen kan hamna i någon speciell vibrationsnivå är proportionell mot kvadraten på den (vertikala) överlappningen av vibrationsvågfunktionerna i det ursprungliga och slutliga tillståndet (se avsnittet Kvantmekanisk formulering nedan). I det elektroniska exciterade tillståndet slappnar molekyler snabbt av till den lägsta vibrationsnivån av det lägsta elektroniska excitationstillståndet ( Kashas regel ), och kan därifrån sönderfalla till det elektroniska grundtillståndet via fotonemission. Franck-Condon-principen tillämpas lika på absorption som på fluorescens .

Tillämpligheten av Franck–Condon-principen i både absorption och fluorescens, tillsammans med Kashas regel leder till en ungefärlig spegelsymmetri som visas i figur 2. Vibrationsstrukturen hos molekyler i en kall, gles gas är tydligast synlig på grund av frånvaron av inhomogena breddning av de enskilda övergångarna. Vibroniska övergångar är ritade i figur 2 som smala, lika åtskilda Lorentziska linjeformer. Lika avstånd mellan vibrationsnivåer är endast fallet för parabolpotentialen hos enkla harmoniska oscillatorer, i mer realistiska potentialer, såsom de som visas i figur 1, minskar energiavståndet med ökande vibrationsenergi. Elektroniska övergångar till och från de lägsta vibrationstillstånden kallas ofta 0–0 (noll noll) övergångar och har samma energi i både absorption och fluorescens.

Utveckling av principen

I en rapport publicerad 1926 i Transactions of the Faraday Society , var James Franck bekymrad över mekanismerna för foton-inducerade kemiska reaktioner. Den förmodade mekanismen var exciteringen av en molekyl av en foton, följt av en kollision med en annan molekyl under den korta excitationsperioden. Frågan var om det var möjligt för en molekyl att brytas in i fotoprodukter i ett enda steg, absorptionen av en foton, och utan en kollision. För att en molekyl ska brytas sönder måste den från fotonen få en vibrationsenergi som överstiger dissociationsenergin, det vill säga energin för att bryta en kemisk bindning. Men, som var känt vid den tiden, kommer molekyler endast att absorbera energi som motsvarar tillåtna kvantövergångar, och det finns inga vibrationsnivåer över dissociationsenerginivån för den potentiella brunnen . Högenergifotonabsorption leder till en övergång till ett högre elektroniskt tillstånd istället för dissociation. När han undersökte hur mycket vibrationsenergi en molekyl kan förvärva när den exciteras till en högre elektronisk nivå, och om denna vibrationsenergi kan räcka för att omedelbart bryta isär molekylen, ritade han tre diagram som representerar de möjliga förändringarna i bindningsenergin mellan den lägsta elektroniska tillstånd och högre elektroniska tillstånd.

Diagram I. visar en stor försvagning av bindningen vid en övergång från det normala tillståndet n till de exciterade tillstånden a och a' . Här har vi D > D' och D' > D". Samtidigt rör sig kärnornas jämviktsposition med exciteringen till högre värden på r . Om vi går från jämviktspositionen (minimum av potentiell energi) för n kurva vertikalt [understrykning tillagd] uppåt till a-kurvorna i diagram I. partiklarna kommer att ha en potentiell energi större än D' och kommer att flyga isär. I detta fall har vi en mycket stor förändring i oscillationsenergin vid excitation av ljus. ..

— James Franck, 1926

James Franck insåg att förändringar i vibrationsnivåer kan vara en konsekvens av excitationens ögonblickliga natur till högre elektroniska energinivåer och en ny jämviktsposition för den nukleära interaktionspotentialen. Edward Condon utökade denna insikt bortom fotoreaktioner i en Physical Review -artikel från 1926 med titeln "A Theory of Intensity Distribution in Band Systems". Här formulerar han den semiklassiska formuleringen på ett sätt som ganska liknar dess moderna form. Den första gemensamma hänvisningen till både Franck och Condon när det gäller den nya principen visas i samma nummer 1926 av Physical Review i en artikel om bandstrukturen för kolmonoxid av Raymond Birge .

Figur 5. Figur 1 i Edward Condons första publikation om vad som nu är Franck–Condon-principen [Condon 1926]. Condon valde att lägga över potentialkurvorna för att illustrera metoden för att uppskatta vibrationsövergångar.

Kvantmekanisk formulering

Betrakta en elektrisk dipolövergång från det initiala vibrationstillståndet ( υ ) för den jordelektroniska nivån ( ε ), $|\epsilon v\rangle$ , till något vibrationstillstånd ( υ ′) av ett exciterat elektroniskt tillstånd ( ε ′), $|\epsilon 'v'\rangle$ (se bra–ket notation ). Den molekylära dipoloperatorn μ bestäms _av laddningen (−e ) och placeringen ( r _i ) för elektronerna samt laddningarna (+ Zj _e ) och lägen ( Rj ) för kärnorna :

{\boldsymbol {\mu }}={\boldsymbol {\mu }}_{e}+{\boldsymbol {\mu }}_{N}=-e\sum \limits _{i}{\ fetsymbol {r}}_{i}+e\sum \limits _{j}Z_{j}{\boldsymbol {R}}_{j}.

Sannolikhetsamplituden P för övergången mellan dessa två tillstånd ges av

P=\left\langle \psi '\right|{\boldsymbol {\mu }}\left|\psi \right\rangle =\int {\psi '^{*}}{\boldsymbol {\mu }}\psi \,d\tau ,

där $\psi$ och $\psi '$ är de övergripande vågfunktionerna för det initiala respektive slutliga tillståndet. De övergripande vågfunktionerna är produkten av individuella vibrationsfunktioner (beroende på rumsliga koordinater för kärnorna) och elektroniska rymd- och spinnvågfunktioner :

\psi =\psi _{e}\psi _{v}\psi _{s}.

Denna separation av de elektroniska och vibrationella vågfunktionerna är ett uttryck för Born–Oppenheimer-approximationen och är det grundläggande antagandet av Franck–Condon-principen. Att kombinera dessa ekvationer leder till ett uttryck för sannolikhetsamplituden i termer av separat elektroniskt utrymme, spinn och vibrationsbidrag:

{\ledisplaystyle\ Plelang }'\psi _{v}'\psi _{s}'\right|{\boldsymbol {\mu }}\left|\psi _{e}\psi _{v}\psi _{s}\right \rangle =\int \psi _{e}'^{*}\psi _{v}'^{*}\psi _{s}'^{*}({\boldsymbol {\mu}}_{e }+{\boldsymbol {\mu }}_{N})\psi _{e}\psi _{v}\psi _{s}\,d\tau }

=\

=\underbrace {\int \psi _{v}'^{*}\psi _{v}\,d\tau _{n}} _{\displaystyle {{\text{Franck–Condon}} \atop {\text{faktor}}}}\underbrace {\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}} _{\displaystyle {{\text{orbital}} \atop {\text{markeringsregel}}}}\underbrace {\int \psi _{s}'^{*}\psi _{s }\,d\tau _{s}} _{\displaystyle {{\text{spin}} \atop {\text{markeringsregel}}}}+\underbrace {\int \psi _{e}'^{ *}\psi _{e}\,d\tau _{e}} _{\displaystyle 0}\int \psi _{v}'^{*}{\boldsymbol {\mu}}_{N}\ psi _{v}\,d\tau _{v}\int \psi _{s}'^{*}\psi _{s}\,d\tau _{s}.

Den spinnoberoende delen av den initiala integralen är här approximerad som en produkt av två integraler:

\iint \psi _{v}'^{*}\psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\psi _{v }\,d\tau _{e}d\tau _{n}\approx \int \psi _{v}'^{*}\psi _{v}\,d\tau _{n}\int \ psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}.

Denna faktorisering skulle vara exakt om integralen $\int \psi _{e}'^{*}{\boldsymbol {\mu }}_{e}\psi _{e}\,d\tau _{e}$ över elektronernas rumsliga koordinater skulle inte bero på kärnkoordinaterna. I Born–Oppenheimer-approximationen beror dock $\psi _{e}$ och $\psi '_{e}$ (parametriskt) på kärnkoordinaterna, så att integralen ( en så kallad övergångsdipolyta ) är en funktion av nukleära koordinater. Eftersom beroendet vanligtvis är ganska jämnt försummas det (dvs antagandet att övergångsdipolytan är oberoende av kärnkoordinater, kallad Condon- approximation tillåts ofta).

Den första integralen efter plustecknet är lika med noll eftersom elektroniska vågfunktioner i olika tillstånd är ortogonala. Återstående är produkten av tre integraler. Den första integralen är vibrationsöverlappningsintegralen, även kallad Franck-Condon-faktorn . De återstående två integralerna som bidrar till sannolikhetsamplituden bestämmer de elektroniska spatiala och spinnvalsreglerna.

Franck–Condon-principen är ett uttalande om tillåtna vibrationsövergångar mellan två olika elektroniska tillstånd; andra kvantmekaniska urvalsregler kan minska sannolikheten för en övergång eller helt förbjuda den. Roterande urvalsregler har försummats i ovanstående härledning. Rotationsbidrag kan observeras i gasspektra men är starkt undertryckta i vätskor och fasta ämnen.

Det bör vara klart att den kvantmekaniska formuleringen av Franck-Condon-principen är resultatet av en serie approximationer, huvudsakligen antagandet om elektrisk dipolövergång och Born-Oppenheimer-approximationen. Svagare magnetiska dipoler och elektriska fyrpoliga elektroniska övergångar tillsammans med den ofullständiga giltigheten av faktoriseringen av den totala vågfunktionen till nukleära, elektroniska rumsliga och spinnvågsfunktioner gör att urvalsreglerna, inklusive Franck-Condon-faktorn, inte strikt följs. För varje given övergång bestäms värdet av P av alla urvalsregler, men spinnval är den största bidragsgivaren, följt av elektroniska urvalsregler. Franck –Condon-faktorn modulerar endast svagt intensiteten av övergångar, dvs den bidrar med en faktor i storleksordningen 1 till intensiteten för band vars storleksordning bestäms av de andra urvalsreglerna. Tabellen nedan visar intervallet av extinktionskoefficienter för möjliga kombinationer av tillåtet och förbjudet spinn och omloppsvalsregler.

**Intensiteter av elektroniska övergångar**
	Område för extinktionskoefficientvärden (ε) ( mol ⁻¹ cm ⁻¹ )
Spinn och orbitalt tillåtet	10 ³ till 10 ⁵
Spinn tillåten men orbitalt förbjuden	⁰ 10 till 10 ³
Spinn förbjuden men orbitalt tillåten	10 ⁻⁵ till 10 ⁰

Franck-Condon metaforer i spektroskopi

Franck-Condon-principen, i sin kanoniska form, gäller endast förändringar i vibrationsnivåerna hos en molekyl under loppet av en förändring av elektroniska nivåer genom antingen absorption eller emission av en foton. Den fysiska intuitionen av denna princip är förankrad av tanken att kärnkoordinaterna för atomerna som utgör molekylen inte hinner förändras under den mycket korta tid som en elektronisk övergång involverar. Denna fysiska intuition kan dock rutinmässigt utvidgas till interaktioner mellan ljusabsorberande eller emitterande molekyler ( kromoforer ) och deras miljö. Franck-Condon-metaforer är lämpliga eftersom molekyler ofta interagerar starkt med omgivande molekyler, särskilt i vätskor och fasta ämnen, och dessa interaktioner modifierar kromoforens nukleära koordinater på sätt som är nära analoga med de molekylära vibrationer som anses av Franck-Condon-principen.

Figur 6. Energidiagram av en elektronisk övergång med fononkoppling längs konfigurationskoordinaten qi , en normalmod för gittret _. De uppåtriktade pilarna representerar absorption utan fononer och med tre fononer. De nedåtriktade pilarna representerar den symmetriska processen i emission.

Franck–Condon princip för fononer

Den närmaste Franck-Condon-analogin beror på interaktionen mellan fononer ( kvanta av gittervibrationer ) med de elektroniska övergångarna av kromoforer inbäddade som föroreningar i gittret. I denna situation kan övergångar till högre elektroniska nivåer ske när fotonens energi motsvarar den rent elektroniska övergångsenergin eller den rent elektroniska övergångsenergin plus energin hos en eller flera gitterfononer. I lågtemperaturapproximationen sker emissionen från nollfononnivån i det exciterade tillståndet till nollfononnivån i grundtillståndet eller till högre fononnivåer i grundtillståndet. Precis som i Franck-Condon-principen, bestäms sannolikheten för övergångar som involverar fononer av överlappningen av fononvågfunktionerna vid de initiala och slutliga energinivåerna. För Franck–Condon-principen som tillämpas på fononövergångar ersätts etiketten för den horisontella axeln i figur 1 i figur 6 med konfigurationskoordinaten för ett normalt läge . Gitterläget $q_{i}$ potentiell energi i figur 6 representeras som den för en harmonisk oscillator, och avståndet mellan fononnivåer ( $\hbar \Omega _{i}$ ) bestäms av gitterparametrar. Eftersom energin hos enstaka fononer i allmänhet är ganska liten, kan noll- eller få-fononövergångar endast observeras vid temperaturer under cirka 40 kelvin .

Se Zero-phonon line och phonon sidband för ytterligare detaljer och referenser.

Franck–Condons princip i lösning

Figur 7. Energidiagram som illustrerar Franck-Condon-principen som tillämpas på solvatisering av kromoforer. De paraboliska potentialkurvorna symboliserar interaktionsenergin mellan kromoforerna och lösningsmedlet. Gauss-kurvorna representerar fördelningen av denna interaktionsenergi.

Franck-Condon-överväganden kan också tillämpas på de elektroniska övergångarna av kromoforer lösta i vätskor. I denna användning av Franck-Condon-metaforen fortsätter kromoforernas vibrationsnivåer, såväl som interaktioner mellan kromoforerna med fononer i vätskan, att bidra till strukturen av absorptions- och emissionsspektra, men dessa effekter betraktas separat och oberoende av.

Betrakta kromoforer omgivna av lösningsmedelsmolekyler . Dessa omgivande molekyler kan interagera med kromoforerna, särskilt om lösningsmedelsmolekylerna är polära . Denna association mellan lösningsmedel och löst ämne kallas solvatisering och är en stabiliserande interaktion, det vill säga lösningsmedelsmolekylerna kan röra sig och rotera tills energin i interaktionen minimeras. Interaktionen i sig involverar elektrostatiska krafter och van der Waals krafter och kan även inkludera vätebindningar . Franck–Condons principer kan tillämpas när interaktionerna mellan kromoforen och de omgivande lösningsmedelsmolekylerna är olika i marken och i det exciterade elektroniska tillståndet. Denna förändring i växelverkan kan till exempel uppstå på grund av olika dipolmoment i dessa två tillstånd. Om kromoforen startar i sitt grundtillstånd och är nära jämvikt med de omgivande lösningsmedelsmolekylerna och sedan absorberar en foton som tar den till det exciterade tillståndet, kommer dess interaktion med lösningsmedlet att vara långt ifrån jämvikt i det exciterade tillståndet. Denna effekt är analog med den ursprungliga Franck-Condon-principen: den elektroniska övergången är mycket snabb jämfört med kärnornas rörelse - omarrangemang av lösningsmedelsmolekyler i fallet med solvatisering. Vi talar nu om en vertikal övergång, men nu är den horisontella koordinaten lösningsmedel-löst ämne interaktionsutrymme. Denna koordinataxel betecknas ofta som "Solvation Coordinate" och representerar, något abstrakt, alla relevanta rörelsedimensioner för alla de interagerande lösningsmedelsmolekylerna.

I den ursprungliga Franck–Condon-principen, efter den elektroniska övergången, börjar de molekyler som hamnar i högre vibrationstillstånd omedelbart att slappna av till det lägsta vibrationstillståndet. Vid solvatisering kommer lösningsmedelsmolekylerna omedelbart att försöka ordna om sig själva för att minimera interaktionsenergin. Hastigheten för lösningsmedelsrelaxation beror på lösningsmedlets viskositet . Om man antar att lösningsmedelsrelaxationstiden är kort jämfört med livslängden för det elektroniska exciterade tillståndet, kommer emissionen att ske från det lägsta lösningsmedelsenergitillståndet i det exciterade elektroniska tillståndet. För småmolekylära lösningsmedel som vatten eller metanol vid omgivningstemperatur är lösningsmedlets relaxationstid i storleksordningen några tiotals pikosekunder medan livstiderna för kromoforexciterade tillstånd sträcker sig från några pikosekunder till några nanosekunder . Omedelbart efter övergången till det jordade elektroniska tillståndet måste lösningsmedelsmolekylerna också ordna om sig själva för att rymma den nya elektroniska konfigurationen av kromoforen. Figur 7 illustrerar Franck-Condon-principen som tillämpas på solvation. När lösningen belyses av ljus som motsvarar den elektroniska övergångsenergin kommer en del av kromoforerna att flyttas till det exciterade tillståndet. Inom denna grupp av kromoforer kommer det att finnas en statistisk fördelning av lösningsmedel-kromoforinteraktionsenergier, representerade i figuren av en Gaussisk fördelningsfunktion . Lösningsmedel-kromoforinteraktionen ritas som en parabolisk potential i båda elektroniska tillstånden. Eftersom den elektroniska övergången är väsentligen momentan på tidsskalan för lösningsmedelsrörelse (vertikal pil), är samlingen av exciterade tillståndskromoforer omedelbart långt ifrån jämvikt. Omarrangemanget av lösningsmedelsmolekylerna enligt den nya potentiella energikurvan representeras av de böjda pilarna i figur 7. Observera att medan de elektroniska övergångarna är kvantiserade, behandlas kromofor-lösningsmedelsinteraktionsenergin som ett klassiskt kontinuum på grund av det stora antalet inblandade molekyler. Även om emission avbildas som att äga rum från minimum av interaktionspotentialen för det exciterade tillståndet kromofor-lösningsmedel, kan betydande emission ske innan jämvikt uppnås när lösningsmedlets viskositet är hög eller livslängden för det exciterade tillståndet är kort. Energiskillnaden mellan absorberade och emitterade fotoner som visas i figur 7 är solvatiseringsbidraget till Stokes-skiftet .

Se även

Vidare läsning

Franck, J. (1926). "Elementära processer för fotokemiska reaktioner". Transaktioner från Faraday Society . 21 : 536-542. doi : 10.1039/tf9262100536 . Länk
Condon, E. (1926). "En teori om intensitetsfördelning i bandsystem (Meeting abstract)". Fysisk granskning . 27 (5): 640. Bibcode : 1926PhRv...27..637. . doi : 10.1103/PhysRev.27.637 .
Condon, E. (1926). "En teori om intensitetsfördelning i bandsystem". Fysisk granskning . 28 (6): 1182–1201. Bibcode : 1926PhRv...28.1182C . doi : 10.1103/PhysRev.28.1182 . Länk Arkiverad 2011-12-28 på Wayback Machine
Condon, E. (1928). "Kärnrörelser associerade med elektronövergångar i diatomiska molekyler". Fysisk granskning . 32 (6): 858–872. Bibcode : 1928PhRv...32..858C . doi : 10.1103/PhysRev.32.858 . Länk Arkiverad 2011-12-28 på Wayback Machine
Birge, RT (1926). "Bandspektra för kolmonoxid". Fysisk granskning . 28 (6): 1157–1181. Bibcode : 1926PhRv...28.1157B . doi : 10.1103/PhysRev.28.1157 . Länk Arkiverad 2011-12-28 på Wayback Machine
Noyes, WA (1933). "Korrelationen mellan spektroskopi och fotokemi". Recensioner av modern fysik . 5 (4): 280–287. Bibcode : 1933RvMP....5..280N . doi : 10.1103/RevModPhys.5.280 . Länk
Coolidge, A.S., James, HM och Present, RD (1936). "En studie av Franck-Condon-principen". Journal of Chemical Physics . 4 (3): 193–211. Bibcode : 1936JChPh...4..193C . doi : 10.1063/1.1749818 . {{ citera tidskrift }} : CS1 underhåll: flera namn: lista över författare ( länk ) Länk
Herzberg, Gerhard (1971). Spektra och strukturer hos enkla fria radikaler . New York: Dover . ISBN 0-486-65821-X .
Harris, Daniel C.; Michael D. Bertolucci (1978). Symmetri och spektroskopi . New York: Dover. ISBN 0-486-66144-X .
Bernath, Peter F. (1995). Spektra av atomer och molekyler (ämnen i fysikalisk kemi) . Oxford: Oxford University Press . ISBN 0-19-507598-6 .
Atkins, PW ; RS Friedman (1999). Molekylär kvantmekanik . Oxford: Oxford University Press. ISBN 0-19-855947-X .

externa länkar

[1]