Zero-phonon line och phonon sidband

Figur 1. Schematisk representation av absorptionslinjeformen för en elektronisk excitation. Den smala komponenten vid frekvensen ω′ är noll-fononlinjen och den bredare egenskapen är fonon-sidobandet. Vid emission speglas de relativa positionerna för de två komponenterna kring mitten av nollfononlinjen vid ω′.

Noll -fononlinjen och fonon-sidobandet utgör tillsammans linjeformen av individuella ljusabsorberande och emitterande molekyler ( kromoforer ) inbäddade i en transparent fast matris. När värdmatrisen innehåller många kromoforer kommer var och en att bidra med en nollfononlinje och ett fonon sidband till absorptions- och emissionsspektra . De spektra som härrör från en samling identiska kromoforer i en matris sägs vara inhomogent breddade eftersom varje kromofor är omgiven av en något annorlunda matrismiljö som modifierar den energi som krävs för en elektronisk övergång. I en inhomogen fördelning av kromoforer är individuella noll-fononlinje- och fonon-sidobandpositioner därför förskjutna och överlappande.

Figur 1 visar den typiska linjeformen för elektroniska övergångar av individuella kromoforer i en solid matris. Nollfononlinjen är belägen vid en frekvens ω' som bestäms av den inneboende skillnaden i energinivåer mellan mark och exciterat tillstånd samt av den lokala miljön. Fonon sidbandet skiftas till en högre frekvens i absorption och till en lägre frekvens i fluorescens. Frekvensgapet Δ mellan noll-fonon-linjen och toppen av fonon-sidobandet bestäms av Franck-Condon-principerna .

Fördelningen av intensitet mellan noll-fononlinjen och fonon-sidobandet är starkt beroende av temperaturen. Vid rumstemperatur finns det tillräckligt med termisk energi för att excitera många fononer och sannolikheten för noll-fononövergång är nära noll. För organiska kromoforer i organiska matriser blir sannolikheten för en noll-fonon elektronisk övergång endast sannolikt under cirka 40 kelvin , men beror också på styrkan i kopplingen mellan kromoforen och värdgittret.

Energidiagram

Figur 2. Energidiagram för en elektronisk övergång med fononkoppling längs konfigurationskoordinaten

{\displaystyle q_{i}},

ett normalt läge för gittret. De uppåtriktade pilarna representerar absorption utan fononer och med tre fononer. De nedåtriktade pilarna representerar den symmetriska processen i emission.

Figur 3. Representation av tre gitternormalmoder ( i , j , k ) och hur deras intensiteter kombineras vid nollfononfrekvensen, men fördelas inom fononsidebandet på grund av deras olika karakteristiska övertonsoscillatorfrekvenser Ω .

Övergången mellan marken och det exciterade tillståndet bygger på Franck–Condon-principen , att den elektroniska övergången är mycket snabb jämfört med rörelsen i gittret. Energiövergångarna kan sedan symboliseras med vertikala pilar mellan marken och det exciterade tillståndet, det vill säga att det inte finns någon rörelse längs konfigurationskoordinaterna under övergången. Figur 2 är ett energidiagram för tolkning av absorption och emission med och utan fononer i termer av konfigurationskoordinaten $q_{i}$ . Energiövergångarna har sitt ursprung vid den lägsta fononenerginivån i de elektroniska tillstånden. Som visas i figuren uppstår den största vågfunktionsöverlappningen (och därför största övergångssannolikheten) när fotonenergin är lika med energiskillnaden mellan de två elektroniska tillstånden ( $E_{1}-E_{0}$ ) plus tre kvanta av gitterläge $i$ vibrationsenergi ( $\hbar \Omega _{i}$ ). Denna tre-fononövergång speglas i emission när det exciterade tillståndet snabbt sjunker till sin nollpunktsgittervibrationsnivå med hjälp av en strålningsfri process, och därifrån till grundtillståndet via fotonemission. Noll-fononövergången avbildas ha en lägre vågfunktionsöverlappning och därför en lägre övergångssannolikhet.

Utöver Franck-Condon-antagandet, antas tre andra approximationer vanligtvis och är implicita i figurerna. Den första är att varje gittervibrationsläge beskrivs väl av en kvantharmonisk oscillator . Denna approximation antyds i den paraboliska formen av de potentiella brunnarna i figur 2, och i det lika energiavståndet mellan fononenerginivåer. Den andra approximationen är att endast den lägsta (nollpunkts) gittervibrationen exciteras. Detta kallas lågtemperaturapproximationen och innebär att elektroniska övergångar inte härrör från någon av de högre fononnivåerna. Den tredje approximationen är att interaktionen mellan kromoforen och gittret är densamma i både marken och det exciterade tillståndet. Specifikt är den harmoniska oscillatorpotentialen lika i båda tillstånden. Denna approximation, som kallas linjär koppling, representeras i figur 2 av två lika formade paraboliska potentialer och av lika åtskilda fononenerginivåer i både marktillstånd och exciterade tillstånd.

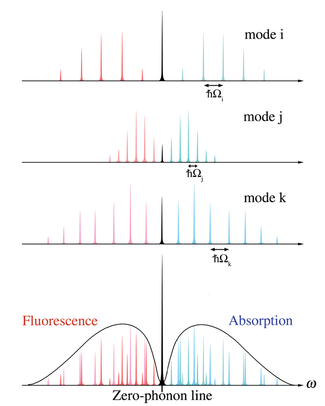
Styrkan hos noll-fononövergången uppstår i överlagringen av alla gitterlägena. Varje gitterläge $m$ har en karakteristisk vibrationsfrekvens ${\Omega }_{m}$ vilket leder till en energiskillnad mellan fononer $\hbar {\Omega }_{ m}$ . När övergångssannolikheterna för alla lägen summeras, adderas alltid noll-fononövergångarna vid det elektroniska origo ( ${\displaystyle E_{1}-E_{0}} ),$ medan övergångarna med fononer bidrar till en fördelning av energier. Figur 3 illustrerar överlagringen av övergångssannolikheter för flera gittermoder. Fononövergångsbidragen från alla gittermoder utgör fonon-sidobandet.

Frekvensseparationen mellan maxima för absorptions- och fluorescensfononsidobanden är fononbidraget till Stokes skift .

Linjeform

₀ Formen på nollfononlinjen är Lorentzian med en bredd som bestäms av det exciterade tillståndets livslängd T ₁₀ enligt Heisenbergs osäkerhetsprincip . Utan inverkan av gittret är kromoforens naturliga linjebredd (full bredd vid halva maximum) γ = 1/ T ₁₀ . Gallret minskar livslängden för det exciterade tillståndet genom att introducera strålningsfria sönderfallsmekanismer. Vid absolut noll är _livslängden för det exciterade tillståndet påverkat av gittret Ti . Över absolut noll kommer termiska rörelser att introducera slumpmässiga störningar i kromoforernas lokala miljö. Dessa störningar förskjuter energin i den elektroniska övergången, vilket introducerar en temperaturberoende breddning av linjebredden. Den uppmätta bredden av en enda kromofors nollfononlinje, den homogena linjebredden, är då γ _h ( T ) ≥ 1/ T ₁ .

Linjeformen på fonons sidoband är den för en Poisson-distribution eftersom det uttrycker ett diskret antal händelser, elektroniska övergångar med fononer, under en tidsperiod. Vid högre temperaturer, eller när kromoforen interagerar starkt med matrisen, är sannolikheten för multifonon hög och fonon sidobandet approximerar en Gaussisk fördelning .

Fördelningen av intensitet mellan noll-fononlinjen och fonon-sidobandet kännetecknas av Debye-Waller-faktorn α.

Analogi till Mössbauer-effekten

Nollfononlinjen är en optisk analogi till Mössbauer-linjerna , som har sitt ursprung i rekylfri emission eller absorption av gammastrålar från kärnorna av atomer bundna i en fast matris. I fallet med den optiska nollfononlinjen är kromoforens position den fysiska parametern som kan störas, medan atomernas momenta kan ändras i gammaövergången. Mer tekniskt sett är nyckeln till analogin symmetrin mellan position och momentum i kvantharmoniska oscillatorns Hamiltonian . Både position och momentum bidrar på samma sätt (kvadratiskt) till den totala energin.

Se även

Friedrich, JJ; D. Haarer (1984). "Fotokemisk hålbränning: En spektroskopisk studie av avslappningsprocesser i polymerer och glasögon". Angewandte Chemie International Edition på engelska . 23 (2): 113–140. doi : 10.1002/anie.198401131 .
Silʹd, O. (1988). Nollfononlinjer och spektral hålbränning i spektroskopi och fotokemi . Berlin: Springer-Verlag. ISBN 978-3-540-19214-5 .

externa länkar