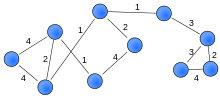
Viktat nätverk

Ett viktat nätverk är ett nätverk där banden mellan noder har vikter tilldelade dem. Ett nätverk är ett system vars element på något sätt är sammankopplade. Elementen i ett system representeras som noder (även kända som aktörer eller hörn) och kopplingarna mellan interagerande element är kända som kopplingar, kanter, bågar eller länkar. Noderna kan vara neuroner, individer, grupper, organisationer, flygplatser eller till och med länder, medan band kan ta formen av vänskap, kommunikation, samarbete, allians, flöde eller handel, för att nämna några.

I ett antal verkliga nätverk har inte alla band i ett nätverk samma kapacitet. Faktum är att slips ofta förknippas med vikter som skiljer dem åt när det gäller deras styrka, intensitet eller kapacitet. Å ena sidan Mark Granovetter (1973) att styrkan hos sociala relationer i sociala nätverk är en funktion av deras varaktighet, känslomässiga intensitet, intimitet och utbyte av tjänster. Å andra sidan, för icke-sociala nätverk, hänvisar vikter ofta till den funktion som utförs av kopplingar, t.ex. kolflödet (mg/m 2 /dag) mellan arter i näringsnät , antalet synapser och gap junctions i neurala nätverk, eller mängden trafik som flyter längs anslutningar i transportnätverk.

Exempel på ett viktat nätverk (vikter kan också visualiseras genom att ge kanter olika bredder)

Genom att registrera styrkan på banden kan ett viktat nätverk skapas (även känt som ett värderat nätverk).

Viktade nätverk används också i stor utsträckning i genomiska och systembiologiska tillämpningar. Till exempel används viktad gensamuttrycksnätverksanalys (WGCNA) ofta för att konstruera ett viktat nätverk bland gener (eller genprodukter) baserat på genuttrycksdata (t.ex. microarray ). Mer generellt viktade korrelationsnätverk definieras genom att mjuktrösklara de parvisa korrelationerna mellan variabler (t.ex. genmätningar).

Mått för viktade nätverk

Även om viktade nätverk är svårare att analysera än om band helt enkelt fanns eller saknades, har ett antal nätverksmått föreslagits för viktade nätverk:

  • Nodstyrka: Summan av vikter kopplade till band som hör till en nod
  • Närhet : Omdefinieras med hjälp av Dijkstras avståndsalgoritm
  • Betweenness : Omdefinieras genom att använda Dijkstras avståndsalgoritm
  • Klustringskoefficienten (global): Omdefinieras med hjälp av ett triplettvärde
  • Klustringskoefficienten (lokal): Omdefinieras genom att använda ett triplettvärde eller använda en algebraisk formel

En teoretisk fördel med viktade nätverk är att de låter en härleda relationer mellan olika nätverksmått (även kända som nätverksbegrepp, statistik eller index). Dong och Horvath (2007) visar till exempel att enkla samband mellan nätverksmått kan härledas i kluster av noder (moduler) i viktade nätverk. För viktade korrelationsnätverk kan man använda vinkeltolkningen av korrelationer för att ge en geometrisk tolkning av nätverksteoretiska begrepp och för att härleda oväntade samband mellan dem Horvath och Dong (2008)

Programvara för att analysera viktade nätverk

Det finns ett antal mjukvarupaket som kan analysera viktade nätverk; se programvara för analys av sociala nätverk . Bland dessa finns den proprietära programvaran UCINET och paketet tnet med öppen källkod.

WGCNA R-paketet implementerar funktioner för att konstruera och analysera viktade nätverk i särskilt viktade korrelationsnätverk.

Se även

  1. ^ Wasserman, S., Faust, K., 1994. Social nätverksanalys: Metoder och tillämpningar. Cambridge University Press, New York, NY.
  2. ^ a b c    A. Barrat och M. Barthelemy och R. Pastor-Satorras och A. Vespignani (2004). "Arkitekturen för komplexa viktade nätverk" . Proceedings of the National Academy of Sciences . 101 (11): 3747–3752. arXiv : cond-mat/0311416 . Bibcode : 2004PNAS..101.3747B . doi : 10.1073/pnas.0400087101 . PMC 374315 . PMID 15007165 .
  3. ^ a b c   Horvath, S., 2011. Vägt nätverksanalys. Tillämpningar inom genomik och systembiologi. Springer bok. ISBN 978-1-4419-8818-8 .
  4. ^   Granovetter, M (1973). "Svaga bands styrka". American Journal of Sociology . 78 (6): 1360–1380. doi : 10.1086/225469 . S2CID 59578641 .
  5. ^    Luczkowich, JJ; Borgatti, SP; Johnson, JC; Everett, MG (2003). "Definiera och mäta trofisk rolllikhet i näringsnät med hjälp av regelbunden ekvivalens". Journal of Theoretical Biology . 220 (3): 303–321. Bibcode : 2003JThBi.220..303L . CiteSeerX 10.1.1.118.3862 . doi : 10.1006/jtbi.2003.3147 . PMID 12468282 .
  6. ^    DJ Watts och Steven Strogatz (juni 1998). "Kollektiv dynamik i "småvärldsnätverk" (PDF) . Naturen . 393 (6684): 440–442. Bibcode : 1998Natur.393..440W . doi : 10.1038/30918 . PMID 9623998 . S2CID 4429113 . Arkiverad från originalet (PDF) 2007-02-21.
  7. ^    Tore Opsahl och Vittoria Colizza och Pietro Panzarasa och Jose J. Ramasco (2008). "Prominens och kontroll: Den viktade rich-club-effekten" . Fysiska granskningsbrev . 101 (16): 168702. arXiv : 0804.0417 . Bibcode : 2008PhRvL.101p8702O . doi : 10.1103/PhysRevLett.101.168702 . PMID 18999722 . S2CID 29349737 . Arkiverad från originalet 2009-11-27 . Hämtad 2009-09-17 .
  8. ^ "Operationalisering av slipsstyrka i sociala nätverk" . 2009-02-06. Arkiverad från originalet 2009-08-24 . Hämtad 2009-09-17 .
  9. ^ a b    Zhang, Bin; Horvath, Steve (2005). "Ett allmänt ramverk för vägd gensamuttrycksnätverksanalys". Statistiska tillämpningar i genetik och molekylärbiologi . 4 : Artikel 17. doi : 10.2202/1544-6115.1128 . PMID 16646834 . S2CID 7756201 .
  10. ^ a b    Langfelder, Peter; Horvath, Steve (2008). "WGCNA: ett R-paket för viktad korrelationsnätverksanalys" . BMC Bioinformatik . 9 : 559. doi : 10.1186/1471-2105-9-559 . PMC 2631488 . PMID 19114008 . open access
  11. ^   Newman, Mark EJ (2001). "Vetenskapliga samarbetsnätverk: II. Kortaste vägarna, viktade nätverk och centralitet" ( PDF) . Fysisk granskning E . 64 (1): 016132. arXiv : cond-mat/0011144 . Bibcode : 2001PhRvE..64a6132N . doi : 10.1103/PhysRevE.64.016132 . PMID 11461356 . Arkiverad (PDF) från originalet 2008-10-10 . Hämtad 2009-09-17 .
  12. ^   Brandes, U (2008). "Om varianter av den kortaste vägen mellan centralitet och deras generiska beräkning". Sociala nätverk . 30 (2): 136–145. CiteSeerX 10.1.1.72.9610 . doi : 10.1016/j.socnet.2007.11.001 .
  13. ^ Opsahl, T; Agneessens, F; Skvoretz, J (2010). "Nodcentralitet i viktade nätverk: Generalisering av grad och kortaste vägar" . Sociala nätverk . 32 (3): 245–251. doi : 10.1016/j.socnet.2010.03.006 . Arkiverad från originalet den 24 juni 2021 . Hämtad 17 juni 2021 .
  14. ^   Tore Opsahl; Pietro Panzarasa (2009). "Klustring i viktade nätverk" . Sociala nätverk . 31 (2): 155–163. CiteSeerX 10.1.1.180.9968 . doi : 10.1016/j.socnet.2009.02.002 . Arkiverad från originalet 2019-07-01 . Hämtad 2009-09-17 .
  15. ^ Dong J, Horvath S (2007) "Förstå nätverksbegrepp i moduler". BMC Systems Biology 2007, 1 juni:24 open access
  16. ^    Dong, Jun; Horvath, Steve (2008). Miyano, Satoru (red.). "Geometrisk tolkning av gensamuttrycksnätverksanalys" . PLOS Computational Biology . 4 (8): e1000117. Bibcode : 2008PLSCB...4E0117H . doi : 10.1371/journal.pcbi.1000117 . PMC 2446438 . PMID 18704157 . open access
  17. ^ "tnet » Programvara" . Tore Opsahl. 12 juni 2011. Arkiverad från originalet den 15 juni 2021 . Hämtad 17 juni 2021 .
Hämtad från " https://en.wikipedia.org/w/index.php?title=Weighted_network&oldid=1137423489 "