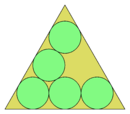
Cirkelpackning i en liksidig triangel
Cirkelpackning i en liksidig triangel är ett packningsproblem inom diskret matematik där målet är att packa n enhetscirklar i minsta möjliga liksidig triangel . Optimala lösningar är kända för n < 13 och för vilket triangulärt antal cirklar som helst, och gissningar är tillgängliga för n < 28 .
En gissning av Paul Erdős och Norman Oler säger att om n är ett triangulärt tal, så har de optimala packningarna av n − 1 och av n cirklar samma sidolängd: det vill säga, enligt gissningen, en optimal packning för n − 1 cirklar kan hittas genom att ta bort en enskild cirkel från den optimala hexagonala packningen av n cirklar. Denna gissning är nu känd för att vara sann för n ≤ 15 .
Minimilösningar för triangelns sidolängd:
| Antal cirklar | Är triangulär | Längd | Område |
|---|---|---|---|
| 1 | Sann | = 3,464... | 5.196... |
| 2 | Falsk | = 5,464... | 12.928... |
| 3 | Sann | = 5,464... | 12.928... |
| 4 | Falsk |
= 6,928... 
|
20.784... |
| 5 | Falsk |
= 7,464...  
|
24.124... |
| 6 | Sann | = 7,464... | 24.124... |
| 7 | Falsk | = 8,928... | 34.516... |
| 8 | Falsk | = 9,293... | 37.401... |
| 9 | Falsk | = 9,464... | 38.784... |
| 10 | Sann | = 9,464... | 38.784... |
| 11 | Falsk | = 10,730... | 49.854... |
| 12 | Falsk | = 10,928... | 51.712... |
| 13 | Falsk | = 11.406... | 56.338... |
| 14 | Falsk | = 11.464... | 56.908... |
| 15 | Sann | = 11.464... | 56.908... |
Ett närbesläktat problem är att täcka den liksidiga triangeln med ett fast antal lika cirklar, med så liten radie som möjligt.
Se även
- Cirkelpackning i en likbent rätvinklig triangel
- Malfatti cirklar , en konstruktion som ger den optimala lösningen för tre cirklar i en liksidig triangel
- ^ a b Melissen, Hans (1993), "Tätaste packningar av kongruenta cirklar i en liksidig triangel", The American Mathematical Monthly , 100 (10): 916–925, doi : 10.2307/2324212 , JSTOR 23242212 , 529 MR 12 .
- ^ Melissen, JBM; Schuur, PC (1995), "Packa 16, 17 eller 18 cirklar i en liksidig triangel" , Diskret matematik , 145 (1–3): 333–342, doi : 10.1016/0012-365X(95)90139-C , MR 1356610 .
- ^ Graham, RL ; Lubachevsky, BD (1995), "Täta packningar av lika skivor i en liksidig triangel: från 22 till 34 och därefter" , Electronic Journal of Combinatorics , 2 : Artikel 1, ca. 39 s. (elektronisk), MR 1309122 .
- ^ Oler, Norman (1961), "A finite packing problem", Canadian Mathematical Bulletin , 4 (2): 153–155, doi : 10.4153/CMB-1961-018-7 , MR 0133065 .
- ^ Payan, Charles (1997), "Empilement de cercles égaux dans un triangle équilatéral. À propos d'une conjecture d'Erdős-Oler", Discrete Mathematics (på franska), 165/166: 555–565, doi : 10.1016 /10.1016 S0012-365X(96)00201-4 , MR 1439300 .
- ^ Nurmela, Kari J. (2000), "Conjecturally optimal coverings of an equilateral triangle with up to 36 equal circles" , Experimental Mathematics , 9 (2): 241–250, doi : 10.1080/10586458.2000.495 , SID 2000.495 , 0ID 2000.495 , 9C 45127090 .