Cirkelpackning i en kvadrat

Cirkelpackning i en kvadrat är ett packningsproblem inom rekreationsmatematiken , där syftet är att packa $n$ enhetscirklar till minsta möjliga kvadrat . På motsvarande sätt är problemet att arrangera $n$ punkter i en enhetskvadrat som syftar till att få den största minimala separationen, $d n$ , mellan punkter. För att konvertera mellan dessa två formuleringar av problemet kommer den kvadratiska sidan för enhetscirklar att vara $.mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num,.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0 0.1em}.mw-parser-output .sfrac .den{border-top:1px solid}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} L = 2 + 2 / d n$ .

Lösningar

Lösningar (inte nödvändigtvis optimala) har beräknats för varje $N \leq 10 000$ . Lösningar upp till $N =20$ visas nedan. Den uppenbara kvadratiska packningen är optimal för 1, 4, 9, 16, 25 och 36 cirklar (de sex minsta kvadrattalen ), men upphör att vara optimal för större rutor från 49 och framåt.

Antal cirklar ( $n$ )	Kvadratisk sidolängd ( $L$ )	$d n$	Taldensitet ( $n / L 2$ )
1	2	∞	0,25
2	$2+{\sqrt {2}}$ ≈ 3,414...	${\sqrt {2}}$ ≈ 1,414...	0,172...
3	$2+{\frac {\sqrt {2}}{2}}+{\frac {\sqrt {6}}{2}}$ ≈ 3,931...	${\sqrt {6}}-{\sqrt {2}}$ ≈ 1,035...	0,194...
4	4	1	0,25
5	$2+2{\sqrt {2}}$ ≈ 4,828...	${\frac {\sqrt {2}}{2}}$ ≈ 0,707...	0,215...
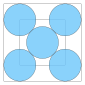
6	$2+{\frac {12}{\sqrt {13}}}$ ≈ 5,328...	${\frac {\sqrt {13}}{6}}$ ≈ 0,601...	0,211...
7	$4+{\sqrt {3}}$ ≈ 5,732...	$4-2{\sqrt {3}}$ ≈ 0,536...	0,213...
8	$2+{\sqrt {2}}+{\sqrt {6}}$ ≈ 5,863...	${\frac {\sqrt {6}}{2}}-{\frac {\sqrt {2}}{2}}$ ≈ 0,518...	0,233...
9	6	0,5	0,25
10	6.747...	0,421... OEIS : A281065	0,220...
11	$3+{\sqrt {2}}+{\frac {\sqrt {6}}{2}}+{\frac {\sqrt {2+4 {\sqrt {2}}}}{2}}$ ≈ 7,022...	0,398...	0,223...
12	$2+15{\sqrt {\frac {2}{17}}}$ ≈ 7.144...	${\frac {\sqrt {34}}{15}}$ ≈ 0,389...	0,235...
13	7.463...	0,366...	0,233...
14	$6+{\sqrt {3}}$ ≈ 7,732...	${\frac {8}{13}}-{\frac {2{\sqrt {3}}}{13}}$ ≈ 0,349...	0,226...
15	$4+{\sqrt {2}}+{\sqrt {6}}$ ≈ 7,863...	${\frac {1}{2}}+{\frac {\sqrt {2}}{2}}-{\frac {\sqrt {3}}{2} }$ ≈ 0,341...	0,243...
16	8	0,333...	0,25
17	8,532...	0,306...	0,234...
18	$2+{\frac {24}{\sqrt {13}}}$ ≈ 8,656...	${\frac {\sqrt {13}}{12}}$ ≈ 0,300...	0,240...
19	8,907...	0,290...	0,240...
20	${\frac {130}{17}}+{\frac {16}{17}}{\sqrt {2}}$ ≈ 8,978...	${\frac {3}{8}}-{\frac {\sqrt {2}}{16}}$ ≈ 0,287...	0,248...

Cirkelpackning i en rektangel

Täta packningar av cirklar i icke-fyrkantiga rektanglar har också varit föremål för många undersökningar.

Se även

Fyrkantig packning i en cirkel

^ ^a ^b Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991). Olösta problem i geometri . New York: Springer-Verlag. s. 108–110 . ISBN 0-387-97506-3 .
^ ^a ^b ^c Eckard Specht (20 maj 2010). "De mest kända packningarna av lika cirklar i en kvadrat" . Hämtad 25 maj 2010 .
^ Lubachevsky, Boris D.; Graham, Ronald L. (2009). "Minsta perimeterrektanglar som omsluter kongruenta icke-överlappande cirklar" . Diskret matematik . Elsevier BV. 309 (8): 1947–1962. doi : 10.1016/j.disc.2008.03.017 . ISSN 0012-365X . S2CID 783236 .
^ Specht, E. (2013). "Högdensitetspackningar av lika cirklar i rektanglar med variabelt bildförhållande". Datorer och operationsforskning . Elsevier BV. 40 (1): 58–69. doi : 10.1016/j.cor.2012.05.011 . ISSN 0305-0548 .

[upg-1] Croft, Hallard T.; Falconer, Kenneth J.; Guy, Richard K. (1991). Olösta problem i geometri . New York: Springer-Verlag. s. 108–110 . ISBN 0-387-97506-3 .

[bestcirclepacking-2] Eckard Specht (20 maj 2010). "De mest kända packningarna av lika cirklar i en kvadrat" . Hämtad 25 maj 2010 .

[Lubachevsky2009-3] Lubachevsky, Boris D.; Graham, Ronald L. (2009). "Minsta perimeterrektanglar som omsluter kongruenta icke-överlappande cirklar" . Diskret matematik . Elsevier BV. 309 (8): 1947–1962. doi : 10.1016/j.disc.2008.03.017 . ISSN 0012-365X . S2CID 783236 .

[Specht2013-4] Specht, E. (2013). "Högdensitetspackningar av lika cirklar i rektanglar med variabelt bildförhållande". Datorer och operationsforskning . Elsevier BV. 40 (1): 58–69. doi : 10.1016/j.cor.2012.05.011 . ISSN 0305-0548 .

Packningsproblem
Abstrakt förpackning	Bin Uppsättning
Cirkelpackning	I en cirkel / liksidig triangel / likbent rät triangel / kvadrat Apollonsk packning Cirkelpackningssats Tammes problem (på sfären)
Sfärförpackning	Apollonisk Ändlig I en sfär I en kub I en cylinder Närpackning Kyss nummer Sfär-packning (Hamming) bunden
Annan 2D-packning	Fyrkantig packning i en kvadrat
Annan 3D-packning	Tetraeder Ellipsoid
Pussel	Conway Slothouber–Graatsma