Bethe–Salpeters ekvation

Bethe –Salpeter-ekvationen (uppkallad efter Hans Bethe och Edwin Salpeter ) beskriver de bundna tillstånden i ett tvåkropps (partiklar) kvantfältteoretisk system i en relativistiskt samvariant formalism. Ekvationen publicerades faktiskt först 1950 i slutet av en artikel av Yoichiro Nambu , men utan härledning.

En grafisk representation av Bethe–Salpeters ekvation, som visar dess rekursiva definition

På grund av dess generella karaktär och dess tillämpning inom många grenar av teoretisk fysik, uppträder Bethe–Salpeters ekvation i många olika former. En form som ganska ofta används inom högenergifysik är

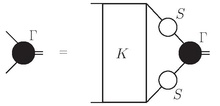
\Gamma ( P,p)=\int \!{\frac {d^{4}k}{(2\pi )^{4}}}\;K(P,p,k)\,S(k-{\ tfrac {P}{2}})\,\Gamma (P,k)\,S(k+{\tfrac {P}{2}})

där Γ är Bethe–Salpeter-amplituden, K interaktionen och S propagatorerna för de två deltagande partiklarna.

I kvantteorin är bundna tillstånd objekt med livslängder som är mycket längre än tidsskalan för interaktionen som styr deras struktur (annars kallas de resonanser ). Således samverkar beståndsdelarna i huvudsak oändligt många gånger. Genom att summera, oändligt många gånger, alla möjliga interaktioner som kan uppstå mellan de två beståndsdelarna, är Bethe–Salpeters ekvation ett verktyg för att beräkna egenskaper hos bundna tillstånd. Dess lösning, Bethe-Salpeters amplitud, är en beskrivning av det bundna tillståndet som övervägs.

Eftersom det kan härledas genom att identifiera bundna tillstånd med poler i S-matrisen , kan det kopplas till den kvantteoretiska beskrivningen av spridningsprocesser och Greens funktioner .

Bethe-Salpeter-ekvationen är ett allmänt kvantfältteoretiskt verktyg, så tillämpningar för den kan hittas i vilken kvantfältteori som helst. Några exempel är positronium (bundet tillstånd för ett elektron - positron - par), excitoner (bundet tillstånd av ett elektron-hål-par ) och mesoner (som kvark -antikvark-bundna tillstånd).

Även för enkla system som positronium kan ekvationen inte lösas exakt, även om den i princip kan formuleras exakt. En klassificering av staterna kan uppnås utan att det behövs en exakt lösning. Om en av partiklarna är betydligt mer massiv än den andra, förenklas problemet avsevärt eftersom man löser Dirac-ekvationen för den lättare partikeln under den tyngre partikelns yttre potential .

Härledning

Utgångspunkten för härledningen av Bethe-Salpeter-ekvationen är Dyson-ekvationen med två partiklar (eller fyra punkter)

G=S_{1}\,S_{2}+S_{1}\,S_{2}\,K_{12}\,G

i momentumrymden, där "G" är tvåpartikelns gröna funktion ${\displaystyle \langle \Omega |\phi _{1}\,\phi _{2}\,\phi _{3}\,\phi _{4}|\Omega \rangle } , "S$ " är de fria propagatorerna och "K" är en interaktionskärna, som innehåller alla möjliga interaktioner mellan de två partiklarna. Det avgörande steget är nu att anta att bundna tillstånd visas som poler i den gröna funktionen. Man antar att två partiklar kommer samman och bildar ett bundet tillstånd med massan "M", detta bundna tillstånd fortplantar sig fritt, och sedan delar sig det bundna tillståndet i sina två beståndsdelar igen. Därför introducerar man Bethe–Salpeter-vågfunktionen ${\displaystyle \Psi =\langle \Omega |\phi _{1}\,\phi _{2}|\psi \rangle } , som är$ en övergångsamplitud av två beståndsdelar $\phi _ {i}$ till ett bundet tillstånd $\psi$ , och gör sedan en ansättning för den gröna funktionen i närheten av polen som

G\approx {\frac {\Psi \;{\bar {\Psi }}}{P^{2}-M^{2}}},

där P är systemets totala rörelsemängd. Man ser att om för detta momentum gäller ekvationen ${\displaystyle P^{2}=M^{2}},$ vilket är exakt Einsteins energi-moment-relation (med fyrmomentet $P_{\mu }=\left(E/c,{\vec {p}}\right)$ och $P^{2 }=P_{\mu }\,P^{\mu }$ ), innehåller den gröna fyrapunktsfunktionen en pol. Om man kopplar in den ansatzen i Dyson-ekvationen ovan och ställer in det totala momentumet "P" så att energi-momentum-relationen håller, uppstår en pol på båda sidor av termen.

{\frac {\Psi \;{\bar {\Psi }}}{P ^{2}-M^{2}}}=S_{1}\,S_{2}+S_{1}\,S_{2}\,K_{12}{\frac {\Psi \;{\ stapel {\Psi }}}{P^{2}-M^{2}}}

Jämföra återstoderna utbyten

\Psi =S_{1}\,S_{2}\,K_{12}\Psi ,\,

Detta är redan Bethe–Salpeters ekvation, skriven i termer av Bethe–Salpeters vågfunktioner. För att erhålla ovanstående form introducerar man Bethe-Salpeters amplituder "Γ"

\Psi =S_{1}\,S_{2}\,\Gamma

och får äntligen

\Gamma =K_{12}\,S_{1}\,S_{2}\,\Gamma

som är nedskrivet ovan, med det explicita momentumberoendet.

Uppskattning av regnbågsstege

En grafisk representation av Bethe–Salpeters ekvation i Ladder-approximation

I princip innehåller interaktionskärnan K alla möjliga två-partikel-irreducerbara interaktioner som kan inträffa mellan de två beståndsdelarna. I praktiska beräkningar måste man alltså modellera det och bara välja en delmängd av interaktionerna. Liksom i kvantfältteorier beskrivs interaktion via utbyte av partiklar (t.ex. fotoner i kvantelektrodynamik , eller gluoner i kvantkromodynamik ), den enklaste interaktionen är utbytet av endast en av dessa kraftpartiklar.

Eftersom Bethe–Salpeters ekvation summerar interaktionen oändligt många gånger, har den resulterande Feynman-grafen formen av en stege (eller regnbåge).

Medan stegapproximationen inom kvantelektrodynamiken orsakade problem med korsningssymmetri och mätinvarians och därför måste inkluderas, men i kvantkromodynamik används denna approximation fenomenologiskt ganska mycket för att beräkna hadronmassor , eftersom den respekterar kiral symmetribrott och därför är en viktig del av genereringen av dessa massor.

Normalisering

Som för alla homogena ekvationer, bestäms lösningen av Bethe–Salpeter-ekvationen endast upp till en numerisk faktor. Denna faktor måste specificeras av ett visst normaliseringstillstånd. För Bethe-Salpeters amplituder görs detta vanligtvis genom att kräva sannolikhetsbevarande (liknande normaliseringen av den kvantmekaniska vågfunktionen ), vilket motsvarar ekvationen

2P_{\mu }={\bar {\ Gamma }}\left({\frac {\partial }{\partial P_{\mu }}}\left(S_{1}\otimes S_{2}\right)-S_{1}\,S_{2} \,\left({\frac {\partial }{\partial P_{\mu }}}\,K\right)\,S_{1}\,S_{2}\right)\Gamma

Normaliseringar av laddningen och energimomentumtensorn för det bundna tillståndet leder till samma ekvation. I stegapproximation beror inte interaktionskärnan på den totala rörelsemängden för Bethe-Salpeter-amplituden, så i detta fall försvinner den andra termen i normaliseringsvillkoret.

Se även

Bibliografi

Många moderna kvantfältteoretiska läroböcker och ett fåtal artiklar ger pedagogiska redogörelser för Bethe–Salpeter-ekvationens sammanhang och användningsområden. Ser:

W. Greiner, J. Reinhardt (2003). Quantum Electrodynamics (3:e upplagan). Springer . ISBN 978-3-540-44029-1 .
ZK Silagadze (1998). "Wick–Cutkosky-modellen: En introduktion". arXiv : hep-ph/9803307 .

Fortfarande en bra introduktion ges av recensionsartikeln av Nakanishi

N. Nakanishi (1969). "En allmän undersökning av teorin om Bethe-Salpeters ekvation" . Framsteg för teoretisk fysik tillägg . 43 : 1–81. Bibcode : 1969PThPS..43....1N . doi : 10.1143/PTPS.43.1 .

För historiska aspekter, se

EE Salpeter (2008). "Bethe–Salpeters ekvation (ursprung)" . Scholarpedia . 3 (11): 7483. arXiv : 0811.1050 . Bibcode : 2008SchpJ...3.7483S . doi : 10.4249/scholarpedia.7483 . S2CID 32913032 .

externa länkar

BerkeleyGW – planvågs pseudopotentialmetod
ExC - plan våg
Fiesta - Gaussisk helelektronmetod