Birkhoffs representationssats

Det här handlar om gitterteori . För andra liknande resultat, se Birkhoffs teorem (disambiguation) .

I matematik , Birkhoffs representation teorem för distributiva gitter påstår att elementen i alla ändliga distributiva gitter kan representeras som finita mängder , på ett sådant sätt att gitter operationer motsvarar fackföreningar och skärningspunkter av mängder. Satsen kan tolkas som att den tillhandahåller en en-till-en-överensstämmelse mellan distributiva gitter och partiella ordningar , mellan kvasi-ordinala kunskapsutrymmen och förorder , eller mellan ändliga topologiska utrymmen och förbeställningar. Den är uppkallad efter Garrett Birkhoff , som publicerade ett bevis på den 1937.

Namnet "Birkhoffs representation theorem" har också applicerats på två andra resultat av Birkhoff, ett från 1935 om representationen av booleska algebror som familjer av mängder slutna under union, skärningspunkt och komplement (så kallade fields of sets , nära besläktade med ringarna av mängder som används av Birkhoff för att representera distributiva gitter), och Birkhoffs HSP-sats som representerar algebror som produkter av irreducible algebror. Birkhoffs representationssats har också kallats grundsatsen för finita distributiva gitter .

Förstå satsen

Många gitter kan definieras på ett sådant sätt att elementen i gittret representeras av mängder, gittrets sammanfogningsoperation representeras av setunion och gittrets mötesoperation representeras av setskärningspunkten. Till exempel har det booleska gittret som definieras från familjen av alla delmängder av en finit mängd denna egenskap. Mer generellt har vilket ändligt topologiskt utrymme ett gitter av mängder som sin familj av öppna mängder. Eftersom uppsättningsförbund och korsningar lyder den fördelande lagen , är varje gitter som definieras på detta sätt ett fördelningsnät. Birkhoffs sats säger att i själva verket alla ändliga distributiva gitter erhållas på detta sätt, och senare generaliseringar av Birkhoffs sats anger en liknande sak för oändliga distributiva gitter.

Exempel

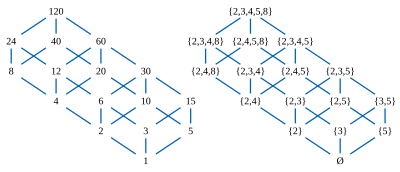
Distributionsgittret av divisorer av 120, och dess representation som uppsättningar av primpotenser.

Betrakta divisorerna för ett sammansatt tal, som (i figuren) 120, delvis ordnade efter delbarhet. Alla två delare på 120, såsom 12 och 20, har en unik största gemensamma faktor 12 ∧ 20 = 4, det största talet som delar dem båda, och en unik minsta gemensamma multipel 12 ∨ 20 = 60; båda dessa tal är också divisorer av 120. Dessa två operationer ∨ och ∧ uppfyller den distributiva lagen , i endera av två ekvivalenta former: ( x ∧ y ) ∨ z = ( x ∨ z ) ∧ ( y ∨ z ) och ( x ∨ y ) ∧ z = ( x ∧ z ) ∨ ( y ∧ z ), för alla x , y och z . Därför bildar divisorerna ett ändligt distributivt gitter .

Man kan associera varje divisor med mängden primpotenser som delar den: 12 är alltså associerad med mängden {2,3,4}, medan 20 är associerad med mängden {2,4,5}. Då är 12 ∧ 20 = 4 associerat med mängden {2,3,4} ∩ {2,4,5} = {2,4}, medan 12 ∨ 20 = 60 är associerad med mängden {2,3,4 } ∪ {2,4,5} = {2,3,4,5}, så sammanfognings- och mötesoperationerna för gittret motsvarar förening och skärning av mängder.

Primpotenserna 2, 3, 4, 5 och 8 som uppträder som element i dessa mängder kan själva vara delvis ordnade efter delbarhet; i denna mindre delordning, 2 ≤ 4 ≤ 8 och det finns inga ordningsrelationer mellan andra par. De 16 uppsättningarna som är associerade med divisorer på 120 är de lägre uppsättningarna av denna mindre delordning, delmängder av element så att om x ≤ y och y tillhör delmängden, så måste x också tillhöra delmängden. Från vilken lägre mängd L som helst kan man återställa den associerade divisorn genom att beräkna den minsta gemensamma multipeln av primpotenserna i L. Således bär den partiella ordningen på de fem primpotterna 2, 3, 4, 5 och 8 tillräckligt med information för att återställa hela det ursprungliga 16-elements delbarhetsgittret.

Birkhoffs teorem säger att detta samband mellan operationerna ∧ och ∨ för divisorgittret och operationerna ∩ och ∪ för de associerade uppsättningarna av primpotenser inte är slumpmässigt och inte beroende av de specifika egenskaperna hos primtal och delbarhet: elementen i vilket ändligt fördelningsgitter som helst kan associeras med lägre uppsättningar av en partiell ordning på samma sätt.

Som ett annat exempel ger tillämpningen av Birkhoffs sats på familjen av delmängder av en n -elementmängd, delvis ordnad genom inkludering, det fria distributionsgittret med n generatorer. Antalet element i detta gitter ges av Dedekind-talen .

Delordningen av sammanfognings-irreducibles

är ett element x sammanfogningsireducerbart om x inte är sammanfogningen av en ändlig uppsättning andra element. På motsvarande sätt x sammanfogningsicke-reducerbar om det varken är bottenelementet i gittret (sammanfogningen av nollelement) eller sammanfogningen av två mindre element. Till exempel, i gittret av divisorer på 120, finns det inget par av element vars sammanfogning är 4, så 4 är sammanfognings-oreducerbar. Ett element x är join-prime om det skiljer sig från bottenelementet, och när x ≤ y ∨ z , antingen x ≤ y eller x ≤ z . I samma gitter är 4 join-prime: närhelst lcm( y , z ) är delbart med 4, måste minst en av y och z själv vara delbar med 4.

I vilket gitter som helst måste ett join-prime-element vara sammanfognings-oreducerbart. På motsvarande sätt är ett element som inte är join-irreducerbart inte join-prime. För, om ett element x inte är sammanfognings-irreducerbart, finns det mindre y och z så att x = y ∨ z . Men då är x ≤ y ∨ z , och x är inte mindre än eller lika med antingen y eller z , vilket visar att det inte är sammanfogat primtal.

Det finns gitter i vilka de sammanfogade primelementen bildar en riktig delmängd av de sammanfogningsireducerbara elementen, men i ett distributivt gitter sammanfaller de två typerna av element. För, anta att x är sammanfogningsicke-reducerbart, och att x ≤ y ∨ z . Denna olikhet är ekvivalent med påståendet att x = x ∧ ( y ∨ z ), och av den distributiva lagen x = ( x ∧ y ) ∨ ( x ∧ z ). Men eftersom x är sammanfogningsicke-reducerbar måste åtminstone en av de två termerna i denna sammanfogning vara x själv, vilket visar att antingen x = x ∧ y (motsvarande x ≤ y ) eller x = x ∧ z (motsvarande x ≤ z ).

Gitterordningen på delmängden av sammanfogningsireducerbara element bildar en partiell ordning ; Birkhoffs teorem säger att själva gittret kan återvinnas från de lägre uppsättningarna av denna partiella ordning.

Birkhoffs sats

Distributivt exempel gitter, med sammanfognings-irreducerbara element a,...,g (skuggade noder). Den lägre mängd en nod motsvarar av Birkhoffs isomorfism visas i blått.

I valfri delordning bildar de lägre uppsättningarna ett gitter där gittrets partiella ordning ges genom inkludering av mängder, sammanfogningsoperationen motsvarar setunion och mötesoperationen motsvarar set skärningspunkt, eftersom sammanslutningar och korsningar bevarar egenskapen att vara en lägre uppsättning. Eftersom uppsättningsförbund och korsningar lyder den fördelande lagen, är detta ett fördelningsgaller. Birkhoffs teorem säger att vilket ändligt fördelningsgitter som helst kan konstrueras på detta sätt.

Sats . Varje ändligt fördelningsgitter L är isomorft mot gittret för lägre uppsättningar av partiell ordning av de sammanfognings-irreducerbara elementen i L .

Det vill säga att det finns en en-till-en ordningsbevarande överensstämmelse mellan element i L och lägre uppsättningar av den partiella ordningen. Den nedre uppsättningen som motsvarar ett element x av L är helt enkelt uppsättningen av sammanfogningsicke-reducerbara element av L som är mindre än eller lika med x , och elementet av L som motsvarar en lägre uppsättning S av sammanfognings-irreducerbara element är sammanfogningen av S .

För varje lägre uppsättning S av sammanfogningsicke-reducerbara element, låt x vara sammanfogningen av S och låt T vara den nedre uppsättningen av sammanfogningsireducerbara element mindre än eller lika med x . Då är S = T . För varje element av S tillhör helt klart T , och varje sammanfognings-irreducerbart element som är mindre än eller lika med x måste (genom join-primalitet) vara mindre än eller lika med en av medlemmarna av S , och måste därför (med antagandet att S är en lägre mängd) tillhör S själv. Omvänt, för varje element x av L , låt S vara de sammanfognings-irreducerbara elementen mindre än eller lika med x , och låt y vara sammanfogningen av S. Då är x = y . För, som en sammanfogning av element som är mindre än eller lika med x , kan y inte vara större än x själv, men om x är sammanfogningsicke-reducerbar så hör x till S medan om x är sammanfogningen av två eller flera sammanfognings-irreducerbara poster de måste återigen tillhöra S , så y ≥ x . Därför är korrespondensen en-till-en och satsen är bevisad.

Ringar av set och förbeställningar

Birkhoff (1937) definierade en ring av uppsättningar som en familj av uppsättningar som är stängd under driften av uppsättningsförbund och fasta korsningar; senare, motiverad av tillämpningar inom matematisk psykologi , kallade Doignon & Falmagne (1999) samma struktur för ett kvasi-ordinalt kunskapsrum . Om uppsättningarna i en ring av uppsättningar är ordnade genom inkludering, bildar de ett fördelningsgitter. Elementen i uppsättningarna kan ges en förordning där x ≤ y närhelst någon uppsättning i ringen innehåller x men inte y . Själva ringen av uppsättningar är då familjen av lägre uppsättningar av denna förbeställning, och varje förbeställning ger upphov till en ring av uppsättningar på detta sätt.

Funktionalitet

Birkhoffs teorem är, som nämnts ovan, en överensstämmelse mellan individuella partiella ordningar och fördelningsgitter. Det kan emellertid också utvidgas till en överensstämmelse mellan ordningsbevarande funktioner av partiella ordningar och gränsade homomorfismer av motsvarande distributiva gitter. Riktningen på dessa kartor är omvänd i denna korrespondens.

Låt 2 beteckna den partiella ordningen på tvåelementsmängden {0, 1}, med ordningsrelationen 0 < 1, och (efter Stanley) låt J(P) beteckna fördelningsgittret för lägre mängder av en ändlig partiell ordning P . Då motsvarar elementen i J(P) en-för-en de ordningsbevarande funktionerna från P till 2 . För, om ƒ är en sådan funktion, bildar ƒ −1 (0) en lägre mängd, och omvänt om L är en lägre mängd kan man definiera en ordningsbevarande funktion ƒ L som mappar L till 0 och som mappar de återstående elementen av P till 1. Om g är någon ordningsbevarande funktion från Q till P , kan man definiera en funktion g * från J(P) till J(Q) som använder sammansättningen av funktioner för att mappa valfritt element L i J(P) till ƒ L ∘ g . Denna sammansatta funktion mappar Q till 2 och motsvarar därför ett element g *( L ) = (ƒ L ∘ g ) −1 (0) av J(Q) . Vidare, för alla x och y i J(P) , g *( x ∧ y ) = g *( x ) ∧ g *( y ) (ett element av Q mappas av g till den lägre mängden x ∩ y om och endast om hör både till uppsättningen av element mappade till x och uppsättningen element mappade till y ) och symmetriskt g *( x ∨ y ) = g *( x ) ∨ g *( y ). Dessutom mappas det nedre elementet i J(P) (funktionen som mappar alla element i P till 0) med g * till det nedre elementet i J(Q) , och det översta elementet i J(P) mappas av g * till det översta elementet i J(Q) . Det vill säga, g * är en homomorfism av avgränsade gitter.

Emellertid motsvarar elementen i P själva en-för-en med gränsade gitterhomomorfismer från J(P) till 2 . För, om x är något element av P , kan man definiera en gränsad gitterhomomorfism j x som mappar alla lägre uppsättningar som innehåller x till 1 och alla andra lägre uppsättningar till 0. Och för varje gitterhomomorfism från J(P) till 2 , elementen i J(P) som är mappade till 1 måste ha ett unikt minimalt element x (träffen av alla element mappade till 1), som måste vara sammanfogningsicke-reducerbart (det kan inte vara sammanfogningen av någon uppsättning element mappade till 0 ), så varje gitterhomomorfism har formen j x för vissa x . Återigen, från vilken som helst avgränsad gitterhomomorfism h från J(P) till J(Q) kan man använda sammansättning av funktioner för att definiera en ordningsbevarande karta h * från Q till P . Det kan verifieras att g ** = g för vilken som helst ordningsbevarande karta g från Q till P och att och h ** = h för varje gränsad gitterhomomorfism h från J(P) till J(Q) .

I kategoriteoretisk terminologi är J en kontravariant hom-funktion J = Hom(—, 2 ) som definierar en dualitet av kategorier mellan å ena sidan kategorin ändliga partiella ordningar och ordningsbevarande kartor, och å andra sidan kategorin ändliga distributiva gitter och avgränsade gitterhomomorfismer.

Generaliseringar

Oändliga distributiva gitter

I ett oändligt distributivt gitter kanske det inte är så att de nedre uppsättningarna av de sammanfognings-irreducerbara elementen är i en-till-en-överensstämmelse med gitterelement. Faktum är att det kanske inte finns några sammanfognings-irreducibles alls. Detta händer till exempel i gittret av alla naturliga tal, ordnade med omvänd ordning av den vanliga delbarhetsordningen (så x ≤ y när y delar x ): vilket tal x som helst kan uttryckas som sammanfogningen av talen xp och xq där p och q är distinkta primtal . Emellertid kan element i oändliga distributiva gitter fortfarande representeras som mängder via Stones representationsteorem för distributiva gitter, en form av stendualitet där varje gitterelement motsvarar en kompakt öppen uppsättning i ett visst topologiskt utrymme . Denna generaliserade representationssats kan uttryckas som en kategoriteoretisk dualitet mellan distributiva gitter och spektralrum (ibland kallade koherenta utrymmen, men inte samma som de koherenta utrymmena i linjär logik ), topologiska utrymmen där de kompakta öppna mängderna är slutna under skärningspunkten och utgör en bas för topologin. Hilary Priestley visade att Stones representationsteorem kunde tolkas som en förlängning av idén att representera gitterelement med lägre uppsättningar av en partiell ordning, med hjälp av Nachbins idé om ordnade topologiska utrymmen. Stenutrymmen med ytterligare en partiell ordning kopplad till topologin via Priestley-separationsaxiom kan också användas för att representera avgränsade distributionsgitter. Sådana utrymmen är kända som Priestley-utrymmen . Vidare, vissa bitopologiska utrymmen , nämligen parvisa stenutrymmen , generaliserar Stones ursprungliga tillvägagångssätt genom att använda två topologier på en uppsättning för att representera ett abstrakt distributivt gitter. Således sträcker sig Birkhoffs representationssats till fallet med oändliga (avgränsade) distributiva gitter på minst tre olika sätt, sammanfattat i dualitetsteori för distributiva gitter .

Medianalgebror och relaterade grafer

Birkhoffs representationssats kan också generaliseras till andra ändliga strukturer än distributiva gitter. I ett distributivt gitter, den självdubbla medianoperationen

ger upphov till en medianalgebra , och gittrets täckande relation bildar en mediangraf . Finita medianalgebror och mediangrafer har en dubbel struktur som uppsättningen lösningar för en instans med 2-tillfredsställelse ; Barthélemy & Constantin (1993) formulerar denna struktur på samma sätt som familjen av initiala stabila uppsättningar i en blandad graf . För ett distributivt gitter har motsvarande blandade graf inga oriktade kanter, och de initiala stabila uppsättningarna är bara de lägre uppsättningarna av den transitiva stängningen av grafen. På motsvarande sätt, för ett distributivt gitter, implikationsgrafen för instansen med 2-tillfredsställelse delas upp i två sammankopplade komponenter , en på de positiva variablerna för instansen och den andra på de negativa variablerna; den transitiva stängningen av den positiva komponenten är den underliggande partiella ordningen för det fördelande gittret.

Finita sammanfogningsfördelande gitter och matroider

Ett annat resultat som är analogt med Birkhoffs representationssats, men som är tillämpligt på en bredare klass av gitter, är Edelmans (1980) sats att vilket ändligt sammanfogat-distributivt gitter som helst kan representeras som en antimatroid , en familj av uppsättningar slutna under fackföreningar men där stängning under korsningar har ersatts av egenskapen att varje icke-tom set har ett borttagbart element.

Se även

Anteckningar

Hämtad från " https://en.wikipedia.org/w/index.php?title=Birkhoff%27s_representation_theorem&oldid=1070360330 "