Digitalt biquad-filter

Vid signalbehandling är ett digitalt biquad-filter ett andra ordningens rekursivt linjärt filter som innehåller två poler och två nollor . "Biquad" är en förkortning av " biquadratic ", vilket hänvisar till det faktum att i Z-domänen är dess överföringsfunktion förhållandet mellan två kvadratiska funktioner :

\ H(z)={\frac {b_{0}+b_ {1}z^{-1}+b_{2}z^{-2}}{a_{0}+a_{1}z^{-1}+a_{2}z^{-2}}}

₀ Koefficienterna är ofta normaliserade så att a = 1:

\ H(z)={\frac {b_{0}+b_ {1}z^{-1}+b_{2}z^{-2}}{1+a_{1}z^{-1}+a_{2}z^{-2}}}

IIR-filter av hög ordning kan vara mycket känsliga för kvantisering av deras koefficienter och kan lätt bli instabila . Detta är ett mycket mindre problem med första och andra ordningens filter; därför implementeras högre ordningens filter typiskt som seriellt kaskadkopplade biquad-sektioner (och ett första ordningens filter om nödvändigt). De två polerna på biquad-filtret måste vara innanför enhetscirkeln för att det ska vara stabilt. I allmänhet gäller detta för alla diskreta filter, dvs alla poler måste vara innanför enhetscirkeln i Z-domänen för att filtret ska vara stabilt.

Genomförande

Direktformulär 1

Den enklaste implementeringen är den direkta formen 1, som har följande skillnadsekvation :

\ y[n]={\frac {1}{a_{0}}}\left(b_{0}x[n]+b_{1}x[n-1]+b_{2}x [n-2]-a_{1}y[n-1]-a_{2}y[n-2]\höger)

eller, om normaliserat:

\ y[n]=b_{0}x[n]+b_{1}x[n-1]+b_{2}x[n-2]-a_{1}y[n-1]-a_{2 }y[n-2]

Här bestämmer $b_{0}$ , $b_{1}$ och $b_{2}$ koefficienterna nollor, och $a_{1}$ , $a_{2}$ bestäm läget för polerna.

Flödesdiagram för biquad-filter i direkt form 1:

När dessa sektioner är kaskadkopplade för filter av storleksordning större än 2, kan effektiviteten av implementeringen förbättras genom att notera att $z^{-1}$ fördröjningen av en sektionsutgång klonas i nästa sektionsinmatning. Två lagringsfördröjningskomponenter kan elimineras mellan sektionerna.

Direktformulär 2

Direktform 2 implementerar samma normaliserade överföringsfunktion som direktform 1, men i två delar:

\ y[n]=b_{0}w[n]+b_{1 }w[n-1]+b_{2}w[n-2],

och använder differensekvationen :

\ w[n]=x[n]-a_{1}w[n-1]-a_{2}w[n-2].

Flödesdiagram för biquad-filter i direkt form 2:

Implementeringen av direkt form 2 behöver bara N fördröjningsenheter, där N är ordningen på filtret – potentiellt hälften så mycket som direkt form 1. Denna struktur erhålls genom att vända ordningen på täljar- och nämnarsektionerna i direkt form 1, eftersom de är i själva verket två linjära system, och kommutativitetsegenskapen gäller. Då kommer man att märka att det finns två kolumner med fördröjningar ( $z^{-1}$ ) som tappar från mittnätet, och dessa kan kombineras eftersom de är redundanta, vilket ger implementeringen som visas.

Nackdelen är att direkt form 2 ökar möjligheten till aritmetiskt spill för filter med högt Q eller resonans. Det har visat sig att när Q ökar, ökar avrundningsbruset för båda direkta formtopologierna utan gränser. Detta beror på att signalen konceptuellt först leds genom ett allpoligt filter (som normalt ökar förstärkningen vid resonansfrekvenserna) innan resultatet av det mättas, sedan passeras genom ett helt nollfilter (som ofta dämpar mycket av det som den allpoliga halvan förstärker).

Den direkta form 2-implementeringen kallas den kanoniska formen, eftersom den använder den minimala mängden fördröjningar, adderare och multiplikatorer, vilket ger samma överföringsfunktion som den direkta form 1-implementeringen.

Transponerade direkta former

Var och en av de två direkta formerna kan transponeras genom att vända flödesdiagrammet utan att ändra överföringsfunktionen. Grenpunkter ändras till somrar och somrar ändras till grenpunkter. Dessa tillhandahåller modifierade implementeringar som åstadkommer samma överföringsfunktion som kan vara matematiskt signifikant i en verklig implementering där precision kan gå förlorad i tillståndslagring.

Skillnadsekvationerna för transponerad direkt form 2 är :

\ y[n]=b_{0}x[n]+s_{1}[n-1],

var

\ s_{1}[n]=s_{2}[n-1]+b_ {1}x[n]-a_{1}y[n]

och

\ s_{2}[n]=b_{2}x[n]-a_{2}y[n].

Transponerad direkt form 1

Den direkta formen 1 transponeras till

Transponerad direkt form 2

Den direkta formen 2 transponeras till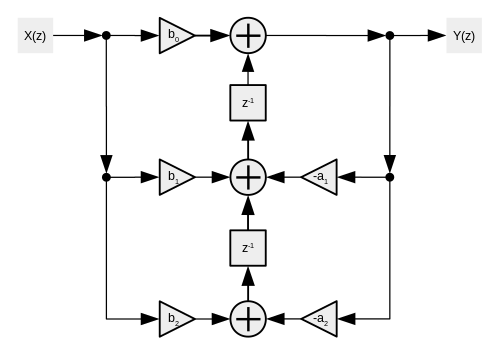

Kvantisering av brus

När ett sampel på n bitar multipliceras med en koefficient på m bitar, har produkten n+m bitar. Dessa produkter ackumuleras vanligtvis i ett DSP-register, tillägg av fem produkter kan behöva 3 spillbitar; detta register är ofta tillräckligt stort för att hålla n+m+3 bitar. z ⁻¹ implementeras genom att lagra ett värde under en samplingstid; detta lagringsregister är vanligtvis n bitar, ackumulatorregistret är avrundat för att passa n bitar, och detta introducerade kvantiseringsbrus.

I det direkta form 1-arrangemanget finns det en enda kvantiserings-/avrundningsfunktion Q(z):

I det direkta form 2-arrangemanget finns även en kvantiserings-/avrundningsfunktion för ett mellanvärde. I en kaskad behöver värdet kanske inte avrundas mellan stegen, men den slutliga utmatningen kan behöva avrundas.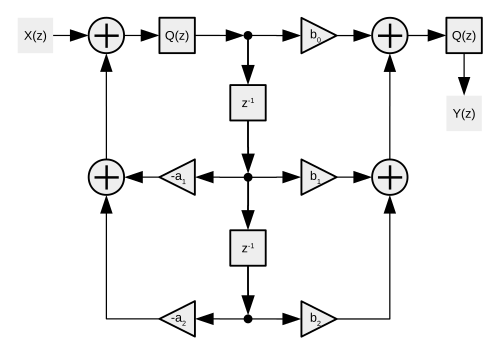

DSP med fast punkt föredrar vanligtvis de icke-transponerade formerna och har en ackumulator med ett stort antal bitar, och är avrundad när den lagras i huvudminnet. Flyttals-DSP föredrar vanligtvis den transponerade formen, varje multiplikation och eventuellt varje addition är avrundade; tilläggen är resultatet med högre precision när båda operanderna har samma storlek.

Se även

externa länkar