Gitternätverk

Den här artikeln handlar om elektroniska filter. För grafen, se gitterdiagram .

Ett symmetriskt gitter är ett elektriskt vågfilter med två portar där diagonalt korsade shuntelement finns - en konfiguration som skiljer det från stegnätverk . Gallrets komponentarrangemang visas i diagrammet nedan. Filteregenskaperna för denna krets utvecklades först med hjälp av bildimpedanskoncept , men senare tillämpades de mer allmänna teknikerna för nätverksanalys på den.

Det finns en duplicering av komponenter i gitternätverket eftersom "serieimpedanserna" (instanser av Za ₎ och "shuntimpedanser" (instanser av Z _b ) båda förekommer två gånger, ett arrangemang som erbjuder ökad flexibilitet till kretsdesignern med en mängd olika svar som kan uppnås. Det är möjligt för gitternätverket att ha egenskaperna för: ett fördröjningsnätverk, ett amplitud- eller faskorrigerande nätverk, ett dispersivt nätverk eller som ett linjärt fasfilter, beroende på valet av komponenter för gitterelementen.

Konfiguration

Den grundläggande konfigurationen av det symmetriska gittret visas i det vänstra diagrammet. En vanlig korthandsversion visas till höger, med prickade linjer som indikerar närvaron av det andra paret av matchande impedanser.

Det är möjligt med denna krets att ha den karakteristiska impedansen specificerad oberoende av dess transmissionsegenskaper, en funktion som inte är tillgänglig för stegfilterstrukturer. Dessutom är det möjligt att utforma kretsen så att den är ett nätverk med konstant motstånd för en rad kretsegenskaper.

Gitterstrukturen kan omvandlas till en obalanserad form (se nedan), för insättning i kretsar med jordplan. Sådana omvandlingar minskar också komponentantalet och minskar komponenttoleranserna.

Det är möjligt att rita om gallret i Wheatstone-bryggkonfigurationen (som visas i artikeln Zobel nätverk ). Detta är dock inte ett lämpligt format för att undersöka egenskaperna hos gitterfilter, särskilt deras beteende i kaskad.

Grundläggande egenskaper

Resultat från bildteori

Filterteorin utvecklades ursprungligen från tidigare studier av transmissionsledningar. I denna teori specificeras en filtersektion i termer av dess utbredningskonstant och bildimpedans (eller karakteristisk impedans).

definieras utbredningsfunktionen, γ , och karakteristisk impedans, Z , av, ₀

$$\gamma =\ln \left[{\ frac {\sqrt {{\frac {Z_{a}}{Z_{b}}}+1}}{\sqrt {{\frac {Z_{a}}{Z_{b}}}-1}}} \right]=2\tanh ^{-1}\left({\sqrt {\frac {Z_{a}}{Z_{b}}}}\right)\qquad {\text{and}}\qquad Z_ {0}={\sqrt {Z_{a}Z_{b}}}$$

När γ och Z ₀ har valts kan lösningar hittas för ${\textstyle {\frac {Z_{a}}{Z_{b}}}}$ och Z _a × Z _b från vilka egenskaperna för Z _a och Zb _{. (I praktiken} kan var och en bestämmas är _Za valen för y och Z ₀ begränsade till de som resulterar i fysiskt realiserbara impedanser för och ₎ Zb . Även om en filterkrets kan ha ett eller flera passband och möjligen flera stoppband (eller dämpningsregioner), betraktas här endast nätverk med ett enda passband.

I kretsens passband är produkten Za _x Zb _R , reell (dvs. Z ₀ är resistiv) och kan likställas med filtrets ₀ avslutande resistans. Så

$$Z_{a}Z_{b}=R_{0}^{2}\qquad {\text{or} }\qquad {\frac {Z_{a}}{R_{0}}}={\frac {R_{0}}{Z_{b}}}\qquad {\text{(för frekvenser i passbandet)} }$$

Det vill säga, impedanserna beter sig som dubbla av varandra inom detta frekvensområde.

I dämpningsområdet för filtret är den karakteristiska impedansen för filtret rent imaginär , och

$$Z_{a}=Z_{b}\qquad \qquad \qquad {\text{(för frekvenser i dämpningsbandet)}}$$

Följaktligen, för att uppnå en specifik karakteristik, väljs reaktanserna inom Za _stoppbandet och Zb _. så att deras resonans- och antiresonansfrekvenser är dubbla av varandra i passbandet och matchar varandra i Filtrets övergångsregion, där en förändring från en uppsättning villkor till en annan sker, kan göras så smal som krävs genom att öka komplexiteten _hos Za _Zb och . Fassvaret för filtret i passbandet styrs av positionerna (mellanrummen) för resonans- och antiresonansfrekvenserna . _för Za _Zb och

definieras de normaliserade parametrarna y ₀ och Z av ₀

$$y_{0}={\sqrt {\frac {Z_{b}}{Z_{a}}}}={\sqrt {\frac {z_{b}}{z_{a}}}}\qquad {\text{and}}\qquad z_{0}={\sqrt {z_{a}z_{b}}}$$

där normaliserade värden z _a = Za _. / R ₀ och z _b = Z _b / R ₀ har införts Parametern y ₀ benämns indexfunktionen och Z ₀ den karakteristiska impedansen för det normaliserade nätverket. Parametrarna y ₀ och Z ₀ approximerar enhet i dämpnings- respektive transmissionsregionerna.

Kaskad av galler

Alla högordningens gitternätverk kan ersättas av en kaskad av enklare gitter, förutsatt att deras karakteristiska impedanser alla är lika med originalets och summan av deras utbredningsfunktioner är lika med originalet.

I det speciella fallet med allpassnätverk (nätverk som endast modifierar faskarakteristiken), kan vilket givet nätverk som helst alltid ersättas av en kaskad av andra ordningens gitter tillsammans med eventuellt ett enda första ordningens gitter.

Oavsett vilka filterkrav som beaktas, resulterar reduktionsprocessen i enklare filterstrukturer, med mindre stränga krav på komponenttoleranser.

Bristerna med bildteorin

Filteregenskaperna som förutsägs av bildteorin kräver ett korrekt avslutat nätverk. Eftersom de nödvändiga avslutningarna ofta är omöjliga att uppnå, används ofta motstånd som avslutningar, vilket resulterar i ett felaktigt filter. Följaktligen kommer kretsens förutsagda amplitud- och fassvar inte längre att vara som bildteorin förutsäger. I fallet med ett lågpassfilter, till exempel, där missanpassningen är mest allvarlig nära gränsfrekvensen, är övergången från passband till stoppband mycket mindre skarp än förväntat.

Bilden nedan illustrerar problemet. Ett gitterfilter, ekvivalent med två sektioner av konstant-k lågpassfilter, har härletts med bildmetoder. (Nätverket är normaliserat, med L = 1 och C = 1 så ₀ R = √ L / C = 1 och ω _c = 2 √   L C = 2 . Den vänstra figuren ger gitterkretsen och den högra figuren ger insättningsförlusten med nätverket avslutat (1) resistivt och (2) i dess korrekta karakteristiska impedanser .

För att minimera felmatchningsproblemet föreslog Otto Julius Zobel och andra olika former av bildfilterslut, men de oundvikliga kompromisserna ledde till att metoden föll i onåd. Det ersattes av de mer exakta metoderna för nätverksanalys och nätverkssyntes .

Resultat härledda genom nätverksanalys

Detta diagram visar den allmänna kretsen för det symmetriska gittret:

Genom nätanalys eller nodalanalys av kretsen kan dess fulla överföringsfunktion hittas. Det är,

$${v_{ \text{out}}}{v_{\text{in}}}}={\frac {Z_{L}(Z_{b}-Z_{a})}{(Z_{a}+Z_{b} )(Z_{S}+Z_{L})+2(Z_{a}Z_{b}+Z_{S}Z_{L})}}}$$

Ingångs- och utgångsimpedanserna ( Z _in och Z _ut ) för nätverket ges av

$${\begin{aligned}Z_{\text{in}}={\frac {2Z_{a}Z_{b}+Z_{L}(Z_{a}+Z_{b}) }{Z_{a}+Z_{b}+2Z_{L}}}\\[1ex]Z_{\text{out}}={\frac {2Z_{a}Z_{b}+Z_{S}( Z_{a}+Z_{b})}{Z_{a}+Z_{b}+2Z_{S}}}\end{aligned}}$$

ZL _, till skillnad från bildteori där utbredningsfunktionen endast förutsäger prestanda exakt när Z _S och är de matchande karakteristiska impedanserna för nätverket.

Ekvationerna kan förenklas genom att göra ett antal antaganden. För det första är nätverk ofta källkodade och avslutade av motstånd med samma värde R ₀ så att Z _S = Z _L = R ₀ och ekvationerna blir

$${\begin{aligned}{\frac {v_{\text{out}}}{v_{\text{in}}}}&={\frac {R_{0}(Z_{ b}-Z_{a})}{2(Z_{a}+R_{0})(Z_{b}+R_{0})}}\\[1ex]Z_{\text{i}}=Z_ {\text{out}}&={\frac {2Z_{a}\,Z_{b}+R_{0}(Z_{a}+Z_{b})}{Z_{a}+Z_{b} +2R_{0}}}\end{aligned}}$$

a _Zb = _: R2 , ₀ ^om impedanserna Za _är och Zb _Z är dubbla av varandra, så att ytterligare förenkling möjlig

$${\frac {v_{\text{out} }}{v_{\text{i}}}}={\frac {R_{0}-Z_{a}}{2(R_{0}+Z_{a})}}={\frac {Z_{ b}-R_{0}}{2(R_{0}+Z_{b})}}\qquad {\text{och}}\qquad Z_{\text{in}}=Z_{\text{out} }=R_{0}$$

så sådana nätverk är nätverk med konstant motstånd.

Slutligen, för normaliserade nätverk, med ₀ R = 1 ,

$${\frac {v_{\ text{ut}}}{v_{\text{in}}}}={\frac {(1-z_{a})}{2(1+z_{a})}}={\frac {(z_ {b}-1)}{2(1+z_{b})}}\qquad \qquad {\text{and}}\qquad z_{\text{in}}=z_{\text{out}}= 1$$

Om impedanserna Za _fassvar och Zb _variabelt (eller de normaliserade impedanserna za _. och zb _ett ) är rena reaktanser, så blir näten all-pass, konstant resistans, med ett platt frekvenssvar men Detta gör dem idealiska som fördröjningsnätverk och fasutjämnare.

När resistorer är närvarande inom Za _. och Zb _kommer , förutsatt att dualitetsvillkoret fortfarande gäller, en krets att ha konstant resistans men ha en variabel amplitudrespons En tillämpning för sådana kretsar är som amplitudutjämnare.

Omvandlingar och ekvivalenser

(Se referenser)

T till galler

Pi till galler

Vanligt serieelement

Vanligt parallellt element

Kombinera två galler till ett

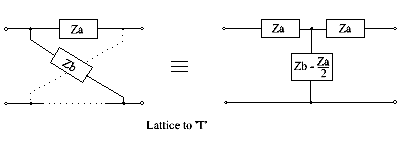
Gitter till T (se även nästa avsnitt)

( Z _b − Za _- ) / 2 omvandling ger endast en realiserbar krets när utvärderingen av ger positivt värderade komponenter. För andra situationer kan det överbryggade-T ge en lösning, som diskuteras i nästa avsnitt.

Obalanserade motsvarigheter

Gallret är en balanserad konfiguration som inte är lämplig för vissa applikationer. I sådana fall är det nödvändigt att omvandla kretsen till en elektriskt ekvivalent obalanserad form. Detta ger fördelar, inklusive minskat antal komponenter och avslappnade kretstoleranser. Den enkla omvandlingsproceduren som visas i föregående avsnitt kan endast tillämpas under en begränsad uppsättning förhållanden – i allmänhet är någon form av bryggad T-krets nödvändig. Många av omvandlingarna kräver inkludering av en idealisk 1:1 transformator, men det finns några konfigurationer som undviker detta krav, och ett exempel visas nedan.

Denna konverteringsprocedur börjar med att använda egenskapen för ett gitter där ett gemensamt serieelement i alla armar kan tas utanför gittret som två serieelement (som visas ovan). Genom att upprepade gånger tillämpa denna egenskap kan komponenter extraheras inifrån gitterstrukturen. Slutligen, med hjälp av Bartletts bisektionssats , uppnås en obalanserad bryggad-T-krets.

I den vänstra figuren har Za _- armen en shuntkondensator, Ca, _och Zb _- armen har en seriekondensator, _Cb . Följaktligen består Z _{a av Ca} parallellt med Za _′ , och Z _b består av Cb _i serie med Z _b ′. Detta kan utvecklas till det obalanserade överbryggade T som visas, Ca _Cb > . _förutsatt att

(En alternativ version av denna krets har T-konfigurationen av kondensatorer ersatta av ett Pi (eller Delta)-arrangemang. För denna T till Pi-konvertering, se ekvationerna i Attenuator (elektronik) ).

När Cb _extraheras > Ca är en alternativ procedur nödvändig, där _{vanliga induktorer först} från gitterarmarna. _Såsom visas, shuntar en induktor La _{Za '} och en induktor Lb _är i serie med Zb ' . Detta leder till den alternativa överbryggade T-kretsen till höger.

Om La _spolar > Lb _. kan induktorn med negativt värde uppnås med hjälp av inbördes kopplade För att uppnå en negativ ömsesidig induktans är de två kopplade induktorerna L1 och L2 lindade "seriehjälpande".

Så slutligen tar den överbryggade T-kretsen formen

Överbryggade-T-kretsar som dessa kan användas i fördröjnings- och faskorrigerande nätverk.

En annan gitterkonfiguration, som innehåller motstånd, visas nedan. Den har shuntmotstånd Ro över Z _a och seriemotstånd Ro som en del av Z _b , som visas i den vänstra bilden. Den konverteras enkelt till en obalanserad bryggad T-krets, som visas till höger.

₀ När Z ₁ Z ₂ = R ² blir det ett konstant motståndsnätverk, som har en insättningsförlust som ges av $T(p)={\frac {R_{0 }}{R_{0}+Z_{1}(p)}}$

₀ När de är normaliserade till 1 ohm är källan, lasten och R alla enhet, så Z ₁ .Z ₂ = 1, och insättningsförlusten blir

$$T(p)={\frac {1}{1+Z_{1}(p)}}$$

Tidigare var kretsar konfigurerade på detta sätt mycket populära som amplitudutjämnare. Till exempel användes de för att korrigera för höga frekvensförluster i telefonkablar och i långa drag av koaxialkabel för tv-installationer.

Ett exempel som visar designproceduren för en enkel utjämnare ges i avsnittet om syntes senare.

All-pass nätverk

(Se tidigare citerade referenser till Zobel, Darlington, Bode och Guillemin. Se även Stewart och Weinberg.)

All-pass-nätverk är en viktig underklass av gitternätverk. De har använts som passiva klumpelementfördröjningar, som faskorrigerare för filternätverk och i dispersiva nätverk. De är nätverk med konstant motstånd så att de kan kaskadkopplas med varandra och med andra kretsar utan att införa missmatchningsproblem.

I fallet med all-pass-nätverk finns det ingen dämpningsområde, så impedanserna Za _och Zb _med (för gittret) är dualer av varandra vid alla frekvenser och Z är ₀ alltid resistiv, lika R ₀ .

dvs.

$$Z_{a}Z_{b}=R_{0}^{2}\qquad \qquad {\text{(vid alla frekvenser)}}$$

För normaliserade nätverk, där ₀ R = 1 , kan överföringsfunktionen T ( p ) skrivas

$$T(p)={\frac {1-z_{ a}(p)}{1+z_{a}(p)}}={\frac {z_{b}(p)-1}{z_{b}(p)+1}}$$

och så

$$z_{a}(p)={\ frac {1-T(p)}{1+T(p)}}\qquad {\text{and}}\qquad z_{b}(p)={\frac {1+T(p)}{1 -T(p)}}$$

I praktiken kan T ( p ) uttryckas som ett förhållande mellan polynom i p , och impedanserna z _a och z _b är också förhållanden mellan polynom i p . För att impedanserna ska vara realiserbara måste de uppfylla Fosters reaktanssats .

De två enklaste all-pass-nätverken är första och andra ordningens gitter. Dessa är viktiga kretsar eftersom, som Bode påpekade, alla högordnings all-pass gitternätverk kan ersättas av en kaskad av andra ordningens nätverk med, möjligen, ett första ordningens nätverk, för att ge identisk respons.

Dessa två enkla, normaliserade gitter har överföringsimpedanser som ges av

$$T_{1}(p)={\frac {- p+c}{p+c}}\qquad \qquad {\text{and}}\qquad T_{2}(p)={\frac {p^{2}-ap+b}{p^{2 }+ap+b}}$$

Kretsarna behandlas mer i detalj i avsnittet om 'Syntes'

Gittersyntes

Nätverkssyntes är processen att härleda en krets för att matcha en vald överföringsfunktion. Alla överföringsfunktioner kan inte realiseras av fysiska nätverk, men för de som kan är gitternätverket alltid en lösning. Med andra ord, om ett symmetriskt tvåterminalsparnätverk överhuvudtaget är realiserbart, är det realiserbart som ett gitternätverk. Detta beror på att gitterstrukturen är den mest allmänna formen av ett nätverk, med färre begränsningar än t.ex. T-, П- eller bryggkopplade-T-nätverk.

När en gitterkrets väl har utvecklats är det ofta önskvärt att omvandla resultatet till en obalanserad form, så att kretsen kan användas i system med jordplan. Dessutom finns det andra fördelar att vinna på omvandlingsprocessen, såsom minskat antal komponenter och mindre stränga toleranser för komponenter. Där en syntesprocedur resulterar i flera möjliga gitterlösningar, väljs vanligtvis den som är lättast att konvertera. Ofta resulterar omvandlingsprocessen i ömsesidigt kopplade induktorer, som visats tidigare, men det är ibland möjligt att undvika dessa helt, om ett högt värde av insättningsförlust kan tolereras, eller om en kombination av parallella kretsar övervägs.

Syntes med z-parametrar

z-parametrar, eller impedansparametrar , är en uppsättning ur familjen av parametrar som definierar ett tvåportsnätverk, med ingångs- och utgångsvärden definierade av I ₁ , I ₂ , V ₁ och V ₂ , som visas i figuren.

Nätverk med två portar

Ekvationer som definierar nätverksbeteende i termer av z-parametrar är

$${\begin{aligned}E_{1}=z_{11}I_{1}+z_{12 }I_{2}\\E_{2}=z_{21}I_{1}+z_{22}I_{2}\end{aligned}}$$

där z-parametrarna definieras under öppna kretsförhållanden (se Impedansparametrar ) så de kallas ibland för "öppna kretsparametrar". De definieras så

$$z_{11}=\left[{\frac {V_{1}}{I_{1 }}}\right]{\text{ med }}I_{2}=0\qquad \qquad z_{12}=\left[{\frac {V_{1}}{I_{2}}}\right] {\text{ med }}I_{1}=0$$

$$z_{21}=\left[{\frac {V_{2}}{I_{1 }}}\right]{\text{ med }}I_{2}=0\qquad \qquad z_{22}=\left[{\frac {V_{2}}{I_{2}}}\right] {\text{ med }}I_{1}=0$$

För det symmetriska gittret är sambanden mellan z-parametrar och gitterimpedanserna lätt att hitta, och de är

$$z_{11}=z_{22}={\frac {Z_{a}+Z_{b} }{2}}\qquad z_{12}=z_{21}={\frac {Z_{b}-Z_{a}}{2}}$$

$$Z_{I}={\sqrt {Z_{a}Z_{b}}}$$

Så,

$$Z_{a}=z_{11}-z_{12}\,,\quad Z_{b}=z_{11}+z_ {12}$$

_ett gitter uppnås genom att helt enkelt fördela delar av ett uttryck i z12 , eller i _z11 och z12 , _direkt till impedanserna Za och _Zb , som i följande exempel _.

Exempel 1

Anse att z ₁₂ ska ges av

$$z_{12}={\frac {p^{5}}{(p^{2}+1)(p^{2 }+2)}}$$

Detta kan utökas till partiella fraktioner, för att ge

$$z_{12}={\frac {p}{p^{2}+1}}-{\frac {4p}{p ^{2}+2}}+p$$

Tilldela termer till Z _a och Z _b , i enlighet därmed, så att ge

$$Z_{a}={\frac {8p}{p^{2}+2}}$$

och $Z_{b}={\frac {2p}{p^{2}+1}}+2p ={\frac {2p^{3}+4p}{p^{2}+1}}$

Gitternätverket som har dessa lösningar för _Za och Zb _visas i den vänstra kretsen nedan . Den kan omvandlas till en obalanserad form genom att för det första extrahera de gemensamma parallella induktorerna och för det andra genom att sedan extrahera seriegemensamma kondensatorer. Detta ger stegnätverket som visas i den högra kretsen.

Syntes från överföringsfunktionen med öppen krets

Den öppna kretsen spänningsförhållande överföringsfunktionen T kan erhållas i termer av z ₁₁ och z ₁₂ , eftersom med I ₂ = 0

$$T={\frac {V_{2}}{V_{1}}}={\frac {z_{12}}{z_{11}}}$$

så från ett uttryck för T , som ger förhållandet z _{12, och} z 11 _, kan det vara möjligt att erhålla kretsar för Za och _Zb .

I praktiken kan T uttryckas i formen

$$T(p)=K\cdot {\frac {N(p)}{D{p}}}$$

där N ( p ) och D ( p ) är polynom i p , den komplexa frekvensvariabeln, och K är en konstant faktor mindre eller lika med enhet.

För ett givet uttryck för T är det ofta möjligt att hitta uttryck (och därmed kretsar för Za _och Zb ₎ , förutsatt att värdet som valts för K är tillräckligt litet.

Nu, för gittret, $T={\frac {z_{11}} {z_{12}}}={\frac {Z_{b}-Z_{a}}{Z_{b}+Z_{a}}}={\frac {1-{\frac {Z_{a}} {Z_{b}}}}{1+{\frac {Z_{a}}{Z_{b}}}}}$

Ordna om ${\frac {Z_{a}}{Z_{b}}}={\frac {1-T}{ 1+T}}={\frac {D-KN}{D+KN}}$

Proceduren utvärderar uttryckets täljare och nämnare som polynom i p och fördelar sedan faktorer till _Za och _Zb . En förlustterm K, med K < 1, kan behövas för att underlätta realiseringen.

Exempel 2

Härled ett gitternätverk med spänningsförhållande överföringsfunktion T ₂ given av

$$T_{2}=K\cdot {\frac {p^{2}+1}{p^{2}+5p+4} }$$

med $K=1$ och

$${\ displaystyle {\begin{aligned}D-KN&=p^{2}+5p+4-p^{2}-1=5p+3\\D+KN&=p^{2}+5p+4+p^ {2}+1=2p^{2}+5p+5\end{aligned}}}$$

$${\frac {Z_{a}}{Z_ {b}}}={\frac {5p+3}{2p^{2}+5p+5}}={\frac {1+3/5p}{1+(2p^{2}+5)/ 5p}}$$

Välj $Z_{a}=1+{\frac {3}{5p}}$ och $Z_{b}= 1+{\frac {2p}{5}}+{\frac {1}{p}}$

Gitterförverkligandet av T ₂ visas nedan till vänster. Det obalanserade nätverket, till höger, erhålls genom att först extrahera de gemensamma seriemotstånden och sedan extrahera kapacitansen.

Exempel 3

En LC-krets har en överföringsfunktion T ₃ given av

$$T_{3}=K\cdot {\frac {(p^{4}+1)}{( p^{2}+1)(p^{2}+2)}}$$

Detta är realiserbart med K = 0,05, alltså

$${\frac {D-KN}{D+KN} }={\frac {0.95(p^{4}+3.1579p^{2}+2.0526}{1.05(p^{4}+2.8571p^{2}+1.9524}}={\frac {Z_{a }}{Z_{b}}}$$

Faktoriserande topp och botten ger

$${\frac {Z_{a}}{Z_{b}}} ={\frac {0,95(p^{2}+0,9153)(p^{2}+2,2426)}{11,05(p^{2}+1,1312)(p^{2}+1,7259)}}$$

Välj, säg,

$$p^{2}+2,2426 )}{(p^{+}1.1312)}}\qquad {\text{and}}\qquad Z_{b}={\frac {p(p+1.7259)}{p^{2}+0.9153}} }$$

Za och Zb _kan realiseras som LC-stegenätverk, där Za _har en shuntinduktor som första element och Zb _{har en} serieinduktor som första element, som visas i den vänstra bilden. Detta gitter kan omvandlas till obalanserad form, med de metoder som angivits tidigare, för att ge komponentvärdena för den högra figuren,

Darlington syntes

Darlingtonmetoden utgör grunden för syntes av förlustfria två terminal-par nätverk med resistiv terminering för föreskrivna överföringsegenskaper.

Nätverk för Darlingtons metod

Bilden visar den grundläggande nätverkskonfigurationen. Den tillhörande överföringsimpedansen är

$$T={\frac {E_{2}}{I_{1}}}$$

Det första steget är att uttrycka ingångsimpedansen Z _I för ett terminerat nätverk i termer av dess z-parametrar. Detta är

$$Z_{I}={\frac {(z_{11}z_{22}-z_{12}^{2 })+z_{11}R}{z_{22}+R}}$$

i vilka _z11 , z22 och _z12 är z-parametrar för nätverket, såsom definierats tidigare _. För ett normaliserat nätverk, sätt R = 1 och ordna om uttrycket så här:

$$Z_{I}=z_{11}\cdot {\frac {(z_{11}z_{ 22}-z_{12}^{2})/z_{11}+1}{z_{22}+1}}$$

I praktiken består Z _I av ett förhållande av två polynom i p:

$$Z_{I}={\frac {N(p)}{D(p)}}={\frac {m_{1}+n_{1}}{m_{2}+n_{2}}}$$

där m ₁ och n ₁ är de jämna och udda delarna av täljarpolynomet respektive och m ₂ och n ₂ är de jämna och udda delarna av nämnarpolynomet.

Omordna $Z_{I}={\frac {m_{1}}{n_{2}} }\cdot {\frac {(n_{1}/m_{1})+1}{(m_{2}/n_{2})+1}}$

Genom att jämföra de två uttrycken för Z _I föreslås följande samband

$$z_{11}={\frac {m_{1}}{n_{2} }}\qquad \qquad z_{22}={\frac {m_{2}}{n_{2}}}\qquad \qquad z_{12}={\frac {\sqrt {m_{1}m_{2 }-n_{1}n_{2}}}{n_{2}}}$$

Exempel 4

Överväg ett nätverk med Z _jag gett av

$$Z_{I}={\frac {2,1351p^{3}+1,915p^{2}+2,4969 p+1}{1,327p^{2}+1,18p+1}}$$

Så,

$${\begin{aligned}m_{1}&=1,915p^{2} +1&n_{1}&=2.1351p^{3}+1\\m_{2}&=1.327p^{2}+1&n_{2}&=1.18p\end{aligned}}$$

Så lösningar för z ₁₁ , z ₂₂ och z ₁₂ är

$$z_{11}={\frac {1,915p^{2}+1}{1,18p}}=1,6229p+{\frac { 1}{1.18p}}$$

dvs z ₁₁ är en induktor på 1,6229H i serie med en kondensator på 1,18F.

$$z_{22}={\frac {1,327p^{2}+1}{1,18p}}=1,1246p+{\frac {1 }{1.18}}$$

dvs z ₂₂ är en induktor på 1,1246H i serie med en kondensator på 1,18F

$${\begin{aligned}z_{12}&={\frac {\sqrt {(1.915p^{2}+1)(1.327p^{2}+1)-(2.1351 p^{3}+2,4969p)}}{1,18p}}\\&={\frac {\sqrt {0,0218p^{4}+0,2957p^{2}+1}}{1,18p}}\ quad ={\frac {0.1479p^{2}+1}{1.18p}}\quad =0.1253p+{\frac {1}{1.18p}}\end{aligned}}$$

Genom att extrahera en serieinduktans på 0,4983 p = (1,6229 p – 1,1246 p ) från z ₁₁ blir det återstående nätverket symmetriskt med

$${\begin{aligned}z_{11}^{\text{(new)}}=z_{ 22}=1.1246p+{\frac {1}{1.18p}}\\z_{12}=0.1253p+{\frac {1}{1.18p}}\end{aligned}}$$

Komponenterna i ett symmetriskt gitter kan beräknas från Za ₌ z ₁₁ − z ₁₂ och Z _b = z ₁₁ + z 12 _.

Så

$$Z_{a}=1,1246p+{\frac {1}{1,18p}}-0,1253p-{\frac { }{1,18p}}=0,9993p,$$

dvs en induktor på 0,9993H.

och

$$Z_{b}=1,1246p+{\frac {1}{1.18p}}+0.1253 frac {1}{1.18p}}=1.2499p+{\frac {2}{1.18p}},$$

dvs en induktor på 1,2499H i serie med en kondensator på 0,59F

Kretsen visas i den vänstra bilden nedan. Den kan enkelt konverteras till den obalanserade formen som visas i den högra bilden. Det är ett lågpassfilter med passbandsrippel på 1,25 dB, med −3 dB vid 0,169 Hz, en noll i stoppbandet vid 0,414 Hz, och stoppbandsdämpning bortom nollfrekvensen under −40 dB.

Syntes av gitternätverk med konstant motstånd

Om impedanserna Za _och Zb _är dubbla, och normaliserade, så att

$$Z_{a}Z_{b}=1$$

då blir bildimpedansen Z _I ett rent motstånd. Ett symmetriskt gitter som uppfyller detta villkor är ett "konstant motståndsgitter".

Ett sådant gitter, avslutat i 1 ohm, visas nedan.

Avslutat Constant-R gitter

Denna har överföringsfunktionen

$${\frac {E_{2}}{E_{1}}}={\frac {E_{2}}{ I_{1}}}=T={\frac {1-Z_{a}}{1+Z_{a}}}$$

där T är överföringsimpedansen med en belastning på 1 ohm i motsats till öppen kretsöverföringsimpedansen _z21 . Ordna om detta, ger

$$Z_{a}={\frac {1-T}{1+T}}$$

Det konstanta motståndsgittret ses således erbjuda ett möjligt tillvägagångssätt för syntesen av överföringsfunktioner.

Det är så att ett gitter med konstant motstånd inte är mindre generellt än vilket annat gitter som helst, vilket innebär att vilken realiserbar överföringsimpedans som helst kan realiseras i form av ett gitter med konstant motstånd. Sådana nätverk är mycket bekväma, eftersom det inte finns någon obalans mellan sektioner eller med resistiva avslutningar. Följaktligen är den totala införingsförlusten för en kaskad av sektioner med konstant motstånd helt enkelt att summera de individuella sektionerna. Omvänt kan en given komplicerad överföringsimpedans delas upp i multiplikativa faktorer, vars individuella gitterförverkliganden, när de är anslutna i kaskad, representerar en syntes av den överföringsimpedansen. Så även om det är möjligt att syntetisera ett enda gitter med komplicerade impedanser Za _och Zb _, är det praktiskt taget lättare att konstruera och ställa in en kaskad av enklare kretsar.

Nätverk med konstant motstånd genomgående

All-pass-nätverk har en konstant förstärkning med frekvens, men de har ett fassvar som varierar på något valt sätt. Till exempel, i fallet med gitterfördröjningsnätverk , är fassvaret linjärt med frekvens över ett specificerat frekvensområde, medan i fallet med gitterfasutjämnare avviker nätverkets fassvar för att kompensera för den icke-linjära fasen svar från ett filternätverk.

Nätverken av första och andra ordningen är de viktigaste eftersom, som Bode påpekade, dessa kan kaskadkopplas efter behov för att ge samma resultat som ett komplicerat högordningsgitter.

Exempel 5

All-pass-svaret av första ordningen är

$$T_{5}={\frac {cp}{c+p}}$$

Denna har en nolla placerad vid +c och en pol vid – c i det komplexa frekvensplanet. Den har ett svar där fasen varierar med frekvensen, men storleken på T ₅ är enhet vid alla frekvenser.

Att använda uttrycket för Z _a som en funktion av T , från tidigare, ger

$$Z_{a}={\frac {1-T_{5}}{1+T_{5}}}={\frac {p}{ c}}$$

Så Z _a är en induktans med värdet 1/ c och följaktligen är Zb en kondensator med värdet 1/ c _. Nätverket, normaliserat till 1 ohm, visas i den vänstra bilden nedan.

Exempel 6

All-pass-svaret av den andra ordningen är

$$T_{6}={\frac {p^{2}-ap+b}{p^{2}+ap+b} }$$

Denna har två nollor placerade vid $x\pm y$ och två poler vid $-x\pm y$ där a = 2 x och b = x ² + y ² . För ett sådant svar varierar fasen med frekvensen, men storleken på T ₆ är enhet vid alla frekvenser.

För denna egenskap återfinns Z _{a från}

$$Z_{a}={\frac {1-T_{6}}{1+T_{6}}}={\frac {ap}{p^{2}+b}}$$

Så Z _a är en parallell kombination av en kapacitans 1/a och en induktans med värdet a / b . På samma sätt Z _b en induktor 1/ a i serie med en kondensator med värdet a / b och nätverket visas till höger nedan.

Gitternätverken kan omvandlas till obalanserade kretsar genom att använda egenskaperna hos gitter med gemensamma element i både _Za och Zb , som _visats tidigare, och Bartletts Bisektionssats.

Första beställningen all-pass

I fallet med andra ordningens nätverk, när a 2 > b (dvs L 1 > L 2 eller C 2 > C 1 eller y > √ 3 x ), är det nödvändigt att använda kretsen som innehåller ömsesidigt kopplade spolar för den andra ordningen all-pass nätverk.

En kaskad av andra ordningens nätverk med, kanske, ett enda första ordningens nätverk, kan användas för att ge en hög ordningens respons. Till exempel ger artikeln Lattice delay-nätverk pol-noll-platser för många all-pass-överföringsfunktioner som närmar sig en linjär faskarakteristik. Den artikeln innehåller också några exempel.

Syntes av amplitudutjämnare

En typisk överföringsväg har ökande förlust med frekvensen och detta kan korrigeras genom att kaskadkoppla systemet med ett utjämningsnät som har en stigande respons med frekvensen. I detta avseende visas en kretskonfiguration som vanligtvis används för att tillhandahålla den nödvändiga utjämningen i figuren märkt 'Galler - grundläggande utjämnarkrets', som gavs tidigare (i avsnittet om 'Obalanserade ekvivalenter'). Som nämnts där, ges insättningsförlusten för den normaliserade kretsen av ${\displaystyle T={\frac {1}{1+Z_{1}(p)}}} ,$ så Z ₁ kan hittas från $Z_{1}(p)={\frac {1}{T(p)}}-1$

Om en viss kvarvarande rippel på svaret tillåts, kan ett enkelt korrigeringsnätverk räcka för Zi _och Z2 _, men denna rippel kan reduceras så mycket som önskas genom att använda mer komplicerade korrigeringsnätverk. Att välja placeringar för polerna och nollor för Z ₁ och Z ₂ kan underlättas av den raka asymptotiska metoden.

Exempel 7

En överföringsfunktion som har en stigande respons över ett begränsat frekvensområde är

$$T_{7}(displaystyle T_{7} )={\frac {3.3333+10.3333p+p^{2}}{30.003+31.003p+p^{2}}}={\frac {(0.3333+p)(10+p)}{(1+ p)(30.003+p)}}$$

Observera att responsen närmar sig enhet vid höga frekvenser. Det kan realiseras som ett bryggt-T eller gitter i vilket Z1 är ett RC _- nätverk.

Z ₁ kan hittas från $Z_{1}(p)={\frac {1}{T(p)}}-1$ . Så $Z_{1}(p)={\frac {26.6697+20.6697p}{3.3333+10.333}p}+p{33}p} }$

Admittansen Y ₁ , där Y ₁ = 1/ Z ₁ kan uttryckas som en fortsatt bråkdel som innehåller fyra termer, alltså

$$Y_^{1}(+frac) 10.333p+3.3333}{20.6697p+26.6697}}=0.04838+{\cfrac {1}{2.2857+{\cfrac {1}{0.4747p+{\cfrac {1}{5.7153}}}}}$$

Så Z ₁ kan realiseras som ett RC-stegnätverk, på Cauer-sättet, och visas som en del av den överbryggade T-kretsen nedan. Z2 är dual av Z1 _{, och så är en RL -} krets, som visas. Motsvarande gitterkrets visas på höger sida.

Lågpassfilter med konstant motstånd

Lågpassfilter av hög ordning kan erhållas genom att kaskadkoppla ett lämpligt antal enklare lågpasssektioner med konstant motstånd.

Den första av dessa lågpasssektioner, med bara en enda pol, har svaret

$$T_{1}={\frac {k_{1}}{p+a}}\qquad so\qquad Z_{a1}={\frac {1-T_{1}}{1+T_{1}}}={\frac {p+(a -k_{1})}{p+(a+k_{1})}}$$

Förutsatt att $k_{1}\leq a$ är detta realiserbar impedans, där Z _a1 är en kombination av två motstånd och en induktor, som visas i den vänstra kretsen nedan, och Z _b1 är den dubbla av Zal . _{_} Detta förvandlas lätt till en obalanserad form, som visas till höger.

Den andra av filtersektionerna, med två poler, har responsen

$$T_{2}=k_{2}{\frac {(p+a)}{(p^{2}+ b_{1}p+b_{0})}}$$

Så gitterimpedansen Z _a2 ges av:

$$Z_{a2 }={\frac {p^{2}+(b_{1}-k_{2})p+(b_{0}-a.k_{2})}{p^{2}+(b_{1} +k_{2})p+(b_{0}+a.k_{2})}}$$

Vissa villkor måste uppfyllas för att säkerställa att detta är ett realiserbart nätverk, vilket är

$$a\geq 0;\qquad k_{2}\leq b_{1};\qquad k_{2}\leq {\frac {b_{0}}{a}}.$$

Också

$$b_{1}-k_{2}\iff k_{2}\leq b_{1}-a.$$

Villkoren sätter gränser för värdet av den konstanta multiplikatorn k ₂ i uttrycket för T ₂ .

Kretsen för gitterelementen Z _a2 visas till vänster, nedan, och den för de dubbla elementen Zb _visas till höger.

Impedans Z _a

Impedans Zb

Komponentvärden för Z _a är,

$${\begin{aligned}R_{1}&={\frac {b_{1}-k_{2}-a}{2k_{2}}}&L&={\frac {1}{2k_ {2}}}\\C&={\frac {2k_{2}}{b_{0}-ab_{1}+a^{2}}}{2ak_{2}}&R_{2}&={\ frac {b_{0}-ab_{1}+a^{2}}{2ak-2}}\end{aligned}}$$

och de för impedanserna Z _b2 är:

$${\begin{aligned}R_{3}&={\frac {1}{R_{1}} }\\R_{4}&={\frac {1}{R_{2}}}\\C_{2}&=L_{1}\quad {\text{and}}\quad L_{2}+ C_{1}\end{aligned}}$$

Den obalanserade versionen av detta galler är som visas nedan:

Genom att kaskadkoppla ett antal av första och andra ordningens kretsar, av den typ som just utvecklats, är det möjligt att härleda högre ordningens lågpassnät av typen:

$$T_{n}(p)={\frac {k}{p ^{n}+b_{n-1}p^{n-1}+\cdots +b_{2}p^{2}+b_{1}p+b_{0}}}$$

De så erhållna gitternäten kan omvandlas till en obalanserad form, förutsatt att värdet på k är tillräckligt litet.

Exempel 8

Ett maximalt platt tredje ordningens normaliserat lågpassfilter har överföringsfunktionen

$$T_{8}={\frac {k}{p^{3}+2p^{2}+2p+1}}$$

Detta kan utökas som

$$T_{8}={\frac {k_{1}}{p+a}} \cdot {\frac {k_{2}(p+a)}{p^{2}+p+1}}\cdot {\frac {1}{p+1}}$$

Så en kaskad av tre gitter kommer att ge det önskade resultatet.

Om en obalanserad krets krävs måste vi acceptera en viss total förlust. Genom att välja k ₁ = k ₂ = a = 0,5 erhålls nätverket som visas nedan. Denna krets har en total förlust på fyra gånger, medan det konventionella LC-stegenätverket inte har någon förlust (men är inte ett konstant motståndsnätverk).

Datorstödda designmetoder

Utvecklingen av stordatorer och sedan persondatorer, under det sista kvartalet av 1900-talet, möjliggjorde en snabb utveckling av numeriska bearbetningstekniker. Till en början användes datorer som ett hjälpmedel för nätverksanalys och sedan till optimeringsmetoder som minimaxmetoden, vid utformningen av fasutjämnare och filter), innan de applicerades direkt på nätverkssyntes. Översikter av mjukvaruutvecklingen inom syntesområdet har getts i Taylor & Huang och Kuo.

Endast ett fåtal av de tidiga syntesprogrammen har handlat om gitternätverk, men S-Filsyn (ett kraftfullt syntes- och analysprogram) ger viss täckning av gitter- och bryggkopplade-T-kretsar.

Tidig historia

Det symmetriska gittret och stegnätverken (det konstanta k-filtret och m-härledda filtret ), var föremål för stort intresse i början av 1900-talet. På den tiden hade den snabbt växande telefonindustrin ett betydande inflytande på utvecklingen av filterteorin, samtidigt som man försökte öka signalöverföringskapaciteten för telefonledningar. George Ashley Campbell var en viktig bidragsgivare till denna nya filterteori, liksom Otto Julius Zobel . De och många kollegor arbetade på laboratorierna hos Western Electric och American Telephone and Telegraph Co., och deras arbete rapporterades i de tidiga upplagorna av Bell System Technical Journal .

Campbell diskuterade gallerfilter i sin artikel från 1922, medan andra tidiga arbetare med intresse för gallret inkluderade Johnson och Bartlett. Zobels artikel om filterteori och design, publicerad ungefär vid denna tidpunkt, nämnde bara kortfattat galler, med hans huvudvikt på stegnätverk. Det var först senare, när Zobel övervägde simulering och utjämning av telefonledningar, som han gav gitterkonfigurationen mer uppmärksamhet. (Den tidens telefonledningar hade en balanserad parkonfiguration med en nominell karakteristisk impedans på 600 ohm, så gitterutjämnaren, med sin balanserade struktur, var särskilt lämplig för användning med dem). Senare arbetare, särskilt Hendrik Wade Bode , gav gitternätverk större framträdande plats i sina filterdesigner.

I de tidiga dagarna baserades filterteori på bildimpedanskoncept , eller bildfilterteori , som var en designmetod som utvecklats från de väletablerade studierna av transmissionsledningar. Filtret ansågs vara en klumpad komponentversion av en sektion av transmissionsledningen och var ett av många inom en kaskad av liknande sektioner. Som nämnts ovan var svagheten med bildfiltermetoden att frekvenssvaret för ett nätverk ofta inte var som förutspått när nätverket avslutades resistivt, istället för av de erforderliga bildimpedanserna. Detta var i grunden en missmatchningsfråga och Zobel övervann det med hjälp av matchande ändsektioner. (se: m-derived filter , mm'-type filter , General mn-type image filter , med senare arbete av Payne och Bode.)

Även om gitterfilter ibland lider av samma problem, kan en rad nätverk med konstant motstånd undvika det helt och hållet.

Under 1930-talet, när tekniker inom nätverksanalys och syntes blev bättre utvecklade, blev det mindre populärt att designa stegfilter med bildmetoder. Trots det fann begreppen fortfarande relevans i vissa moderna mönster. Å andra sidan fortsätter gitternätverk och deras kretsekvivalenter att användas i många tillämpningar.

Se även

• Gitterfasutjämnare
• All-pass filter
• Nätverk med två portar
• Sammansatt bildfilter
• Gitterfördröjningsnätverk
• Stegnätverk