Beat (akustik)

Diagram över slagfrekvens

Inom akustik är ett slag ett interferensmönster mellan två ljud med något olika frekvenser , uppfattat som en periodisk variation i volym vars hastighet är skillnaden mellan de två frekvenserna.

Med stämningsinstrument som kan producera ihållande toner kan beats lätt kännas igen. Att stämma två toner till en unison kommer att ge en märklig effekt: när de två tonerna är nära i tonhöjd men inte identiska, genererar skillnaden i frekvens takten. Volymen varierar som i en tremolo då ljuden omväxlande interfererar konstruktivt och destruktivt. När de två tonerna gradvis närmar sig unisont, saktar slaget ner och kan bli så långsamt att det är omärkligt. När de två tonerna kommer längre ifrån varandra börjar deras taktfrekvens närma sig intervallet för mänsklig tonhöjdsuppfattning, slaget börjar låta som en ton och en kombinationston produceras. Denna kombinationston kan också hänvisas till som en saknad grundton , eftersom slagfrekvensen för två valfria toner är ekvivalent med frekvensen för deras implicita grundfrekvens.

Matematik och fysik av takttoner

Summan (blå) av två sinusvågor (röd, grön) visas när en av vågorna ökar i frekvens. De två vågorna är initialt identiska, sedan ökas den gröna vågens frekvens gradvis med 25 %. Konstruktiv och destruktiv störning kan ses.

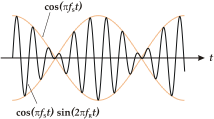
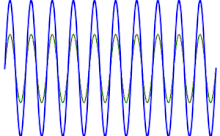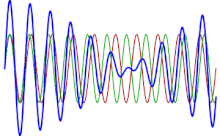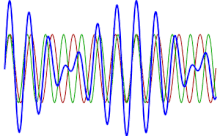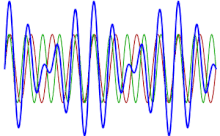
Detta fenomen är mest känt inom akustik eller musik, även om det kan hittas i alla linjära system: "Enligt lagen om överlagring överlagras två toner som låter samtidigt på ett mycket enkelt sätt: man lägger till deras amplituder". Om en graf ritas för att visa funktionen som motsvarar det totala ljudet av två strängar , kan man se att maxima och minima inte längre är konstanta som när en ren ton spelas, utan förändras över tiden: när de två vågorna är nästan 180 grader ur fas upphäver den ena vågens maxima minima för den andra, medan när de är nästan i fas summeras deras maxima, vilket höjer den upplevda volymen.

Det kan bevisas med hjälp av en summa-till-produkt trigonometrisk identitet (se Lista över trigonometriska identiteter ) att enveloppen av maxima och minima bildar en våg vars frekvens är hälften av skillnaden mellan frekvenserna för de två ursprungliga vågorna. Betrakta två sinusvågor med enhetsamplitud :

${\stil {\cos(2\pi f_{1}t)+\cos(2\pi f_{2}t)}={2\cos \left(2\pi {\frac {f_{1}+f_{2 }}{2}}t\right)\cos \left(2\pi {\frac {f_{1}-f_{2}}{2}}t\right)}}$

Om de två ursprungliga frekvenserna är ganska nära (till exempel en skillnad på cirka tolv hertz ), är frekvensen för cosinus på höger sida av uttrycket ovan, det vill säga f ₁ − f ₂ / 2 , ofta för låg för att vara uppfattas som en hörbar ton eller tonhöjd . Istället uppfattas det som en periodisk variation av den första termens amplitud i uttrycket ovan. Man kan säga att den lägre frekvens cosinustermen är en envelope för den högre frekvensen, dvs att dess amplitud är modulerad. Frekvensen för moduleringen är f ₁ + f ₂ / 2 , det vill säga medelvärdet av de två frekvenserna. Det kan noteras att varannan skur i moduleringsmönstret inverteras. Varje topp ersätts av en dalgång och vice versa. Men eftersom det mänskliga örat inte är känsligt för fasen av ett ljud, bara dess amplitud eller intensitet, hörs bara storleken på enveloppen. Därför, subjektivt, verkar frekvensen för enveloppen ha dubbelt så hög frekvens som den modulerande cosinus, vilket betyder att den hörbara slagfrekvensen är:

$f_{\text{beat}}=f_{1}-f_{2}\,$

Detta kan ses på diagrammet intill.

En 110 Hz A sinusvåg (magenta; första 2 sekunderna), en 104 Hz G ♯ sinusvåg (cyan; efter 2 sekunder), deras summa (blå; sista 2 sekunderna) och motsvarande envelopp (röd)

En fysisk tolkning är att när

$\cos \left(2\pi {\frac {f_{1}-f_{2}}{2}}t\right)=1$

de två vågorna är i fas och de interfererar konstruktivt. När det är noll är de ur fas och stör destruktivt. Beats förekommer också i mer komplexa ljud, eller i ljud med olika volymer, även om det inte är så lätt att beräkna dem matematiskt.

För att ett mänskligt öra ska höra slagfenomen bör förhållandet mellan frekvenser vara mindre än ${\displaystyle {\frac {7}{6}}},$ annars uppfattar hjärnan dem som två olika frekvenser [ .

Slag kan också höras mellan toner som är nära, men inte exakt, ett harmoniskt intervall , på grund av att någon överton i den första tonen slår med en överton i den andra tonen. Till exempel, i fallet med perfekt kvint, slår den tredje övertonen (dvs. andra övertonen) i bastonen med den andra övertonen (första övertonen) i den andra tonen. Såväl som med ostämda toner, kan detta även hända med några korrekt inställda lika temperamentintervall på grund av skillnaderna mellan dem och motsvarande justa intonationsintervall : se Harmonic series (musik)#Harmonics and tuning .

Binaurala beats

Binaurala beats

För att uppleva den binaurala beatsuppfattningen är det bäst att lyssna på den här filen med hörlurar på måttlig till svag volym – ljudet ska vara lätt att höra, men inte högt. Ljudet verkar bara pulsera när det hörs genom båda hörlurarna. Tidslängd 10 sekunder

Binaural Beats Baston 200 Hz, slagfrekvens från 7 Hz till 12,9 Hz. Tidslängd 9 minuter.

Ett binauralt slag är en hörselillusion som uppfattas när två olika rentonade sinusvågor , båda med frekvenser lägre än 1500 Hz, med mindre än 40 Hz skillnad mellan dem, presenteras för en lyssnare dikotiskt (en genom varje öra ).

Till exempel, om en 530 Hz ren ton presenteras för en persons högra öra, medan en 520 Hz ren ton presenteras för patientens vänstra öra, kommer lyssnaren att uppfatta hörselillusionen av en tredje ton, förutom de två rena tonerna. toner som presenteras för varje öra. Det tredje ljudet kallas ett binauralt slag och skulle i detta exempel ha en uppfattad tonhöjd som korrelerar med en frekvens på 10 Hz, det vill säga skillnaden mellan 530 Hz och 520 Hz rena toner som presenteras för varje öra.

Binaural-beat perception har sitt ursprung i den inferior colliculus i mellanhjärnan och det överlägsna olivarkomplexet i hjärnstammen , där hörselsignaler från varje öra är integrerade och fäller ut elektriska impulser längs neurala banor genom retikulära formationen upp till mellanhjärnan till thalamus , hörselbarken , och andra kortikala regioner.

Några påstådda fördelar med binaural beats-terapi kan inkludera: minskad stress , minskad ångest , ökat fokus, ökad koncentration, ökad motivation, ökat självförtroende och djupare meditation . Forskning är ofullständig om de kliniska fördelarna med binaural beatterapi; det har hävdats att det är bäst att inte ersätta traditionella behandlingar för stress och ångest med denna typ av intervention förrän avgörande bevis presenteras.

Det finns inga kända biverkningar av att lyssna på binaurala beats, även om långvarig exponering för ljud på eller över 85 decibel kan orsaka hörselnedsättning över tid. Detta är ungefär den bullernivå som genereras av tung trafik.

Används

Musiker använder vanligtvis interferensslag objektivt för att kontrollera stämningen vid unisona , perfekta femte eller andra enkla harmoniska intervall. Stämmare för piano och orgel använder till och med en metod som involverar att man räknar taktslag och siktar på ett visst nummer för ett specifikt intervall.

Kompositören Alvin Lucier har skrivit många stycken som har interferensslag som huvudfokus . Den italienske kompositören Giacinto Scelsi , vars stil grundar sig på mikrotonala svängningar av unisona, utforskade omfattande textureffekterna av interferensslag, särskilt i sina sena verk som fiolsolon Xnoybis (1964) och L'âme ailée / L'âme ouverte (1973) ), som har dem framträdande (Scelsi behandlade och noterade varje sträng av instrumentet som en separat del, så att hans violinsolo är effektivt kvartetter av ensträngade, där olika strängar av fiolen kan spela samma ton samtidigt med mikrotonala skiftningar , så att interferensmönstren genereras). Kompositören Phill Niblocks musik är helt och hållet baserad på slag som orsakas av mikrotonala skillnader. Dataingenjör Toso Pankovski uppfann en metod baserad på hörselstörningar för att avskärma deltagare i auditiva onlinestudier för hörlurar och dikotiskt sammanhang (oavsett om stereokanalerna är blandade eller helt separerade).

Se även

• Autonoma sensoriska meridiansvar (ASMR)
• Konsonans och dissonans
• Gamelan tuning
• Heterodyne
• Moirémönster , en form av rumslig interferens som genererar nya frekvenser.
• Musik och sömn
• Voix céleste

Vidare läsning

•   Thaut, Michael H. (2005). Rytm, musik och hjärnan: vetenskapliga grunder och kliniska tillämpningar ( första i pocketutgåva). New York: Routledge. ISBN 978-0415973700 .
•   Berger, Jonathan; Turow, Gabe, red. (2011). Musik, vetenskap och den rytmiska hjärnan: kulturella och kliniska implikationer . Routledge. ISBN 978-0415890595 .

externa länkar

• Läromedel relaterat till Beat (akustik) på Wikiversity
• Javascript-applet , MIT
• Akustik och vibrationsanimationer , DA Russell, Pennsylvania State University
• En Java-applet som visar bildandet av beats på grund av interferensen av två vågor med något olika frekvenser
• Lissajous Curves: Interaktiv simulering av grafiska representationer av musikaliska intervall, beats, interferens, vibrerande strängar
• The Feynman Lectures on Physics Vol. I Ch. 48: Beats