APL-syntax och symboler

Den här artikeln innehåller APL- källkod . Utan korrekt renderingsstöd kan du se frågetecken, rutor eller andra symboler istället för APL-symboler .

Programmeringsspråket APL är utmärkande genom att vara symboliskt snarare än lexikalt : dess primitiver betecknas med symboler , inte ord. Dessa symboler skapades ursprungligen som en matematisk notation för att beskriva algoritmer. APL-programmerare tilldelar ofta informella namn när de diskuterar funktioner och operatorer (till exempel "produkt" för ×/) men kärnfunktionerna och operatorerna som tillhandahålls av språket betecknas med icke-textuella symboler.

Monadiska och dyadiska funktioner

De flesta symboler betecknar funktioner eller operatorer . En monadisk funktion tar som sitt argument resultatet av att utvärdera allt till sin rätt. (Modereras på vanligt sätt inom parentes.) En dyadisk funktion har ett annat argument, den första dataposten till vänster. Många symboler betecknar både monadiska och dyadiska funktioner, tolkade efter användning. Till exempel ger ⌊3.2 3, det största heltal inte över argumentet, och 3⌊2 ger 2, det lägre av de två argumenten.

Funktioner och operatörer

APL använder termen operator i Heavisides mening som moderator för en funktion i motsats till något annat programmeringsspråks användning av samma term som något som verkar på data, ref. relationsoperatör och operatörer i allmänhet . Andra programmeringsspråk använder också ibland denna term omväxlande med funktion , men båda termerna används i APL mer exakt. Tidiga definitioner av APL-symboler var mycket specifika om hur symboler kategoriserades. Operatorns reducering betecknas till exempel med ett snedstreck och reducerar en array längs en axel genom att lägga in dess funktionsoperand . Ett exempel på reducering : 

×/2 3 4 24
<< Motsvarande resultat i APL >> << Reducera operator / används till vänster 
2×3×4 24

I ovanstående fall modererar operatören reducera eller snedstreck multiplikationsfunktionen . Uttrycket ×/2 3 4 utvärderas till ett skalärt (endast 1 element) resultat genom att reducera en array genom multiplikation. Ovanstående fall är förenklat, tänk dig att multiplicera (lägga till, subtrahera eller dividera) mer än bara några siffror tillsammans. (Från en vektor ×/ produkten av alla dess element.) 

1 0 1\45 67 45 0 67

<< Motsatta resultat i APL >> << Expandera dyadisk funktion \ används till vänster Replikera dyadisk funktion / används till höger >> 
1 0 1/45 0 67 45 67

Ovanstående exempel på dyadiska funktioner [vänster och höger exempel] (med samma / symbol, höger exempel) visar hur booleska värden (0s och 1s) kan användas som vänsterargument för \ expand och / replikera funktionerna för att ge exakt motsatta resultat. På vänster sida expanderas 2-elementsvektorn { 45 67} där booleska nollor förekommer för att resultera i en 3-elementsvektor {45 0 67} — notera hur APL infogade en nolla i vektorn. Omvänt sker raka motsatsen på höger sida — där en 3-elementsvektor blir bara 2-element; booleska nollor tar bort objekt med hjälp av funktionen dyadic / snedstreck . APL-symboler fungerar också på listor (vektorer) av objekt som använder andra datatyper än bara numeriska, till exempel kan en 2-elementsvektor av teckensträngar {"Äpplen" "Apelsiner"} ersätta den numeriska vektorn {45 67} ovan.

Syntaxregler

I APL är prioriteringshierarkin för funktioner eller operatorer strikt positionell: uttryck utvärderas från höger till vänster. APL följer inte det vanliga operatörsföreträdet för andra programmeringsspråk; till exempel, × binder inte sina operander mer "snävare" än + . Istället för operatörsföreträde definierar APL ett begrepp om omfattning .

Omfattningen av en funktion avgör dess argument . Funktioner har lång rätt räckvidd : det vill säga de tar som rätt argument allt till sin rätt. En dyadisk funktion har kort vänster omfattning : den tar som vänsterargument den första databiten till vänster. Till exempel (kolumnen längst till vänster nedan är faktisk programkod från en APL- användarsession , indrag = faktisk användarinmatning , inte indrag = resultat som returneras av APL-tolkare ):

En operatör kan ha funktions- eller dataoperander och utvärdera till en dyadisk eller monadisk funktion. Operatörer har länge lämnat räckvidden. En operatör tar som sin vänstra oper och den längsta funktionen till vänster. Till exempel:

Den vänstra operanden för operatören över varje ¨ är indexfunktionen ⍳ . Den härledda funktionen ⍳¨ används monadiskt och tar som sin högra operand vektorn 3 3 . Den vänstra räckvidden för varje avslutas av reduceringsoperatören , betecknad med snedstrecket . Dess vänstra operand är funktionsuttrycket till vänster: den yttre produkten av lika- funktionen. Resultatet av ∘.=/ är en monadisk funktion. Med en funktions vanliga långa högra omfattning tar den som sitt rätta argument resultatet av ⍳¨3 3. Således

Monadiska funktioner

Namn Notation Menande Unicode-kodpunkt
Rulla ?B Ett heltal valt slumpmässigt från de första B- heltalen U+003F ?
Tak ⌈B Minsta heltal större än eller lika med B U+2308 ⌈
Golv ⌊B Största heltal mindre än eller lika med B U+230A ⌊
Shape, Rho ⍴B Antal komponenter i varje dimension av B U+2374 ⍴
Inte , Tilde ∼B Logisk: ∼1 är 0, ~0 är 1 U+223C ~
Absolutvärde ∣B Storleken på B U+2223 ∣
Indexgenerator, Iota ⍳B Vektor av de första B- heltalen U+2373 ⍳
Exponentiell ⋆B e till B -potentialen U+22C6 ⋆
Negation −B Byter tecken på B U+2212 −
Konjugera +B Den komplexa konjugatet av B (reella tal returneras oförändrade) U+002B +
Signum ×B ¯1 om B <0; O om B = O; 1 om B >0 U+00D7 ×
Ömsesidig ÷B 1 dividerat med B U+00F7 ÷
Ravel, Catenate, Laminat ,B Omformar B till en vektor U+002C ,
Matrix invers , Monadic Quad Divide ⌹B Invers av matris B U+2339 ⌹
Pi gånger ○B Multiplicera med π U+25CB ○
Logaritm ⍟B Naturlig logaritm för B U+235F ⍟
Omkastning ⌽B Vänd element av B längs sista axeln U+233D ⌽
Omkastning ⊖B Vänd element av B längs första axeln U+2296 ⊖
Gradera upp ⍋B Index för B som kommer att ordna B i stigande ordning U+234B ⍋
Gradera ner ⍒B Index för B som kommer att ordna B i fallande ordning U+2352 ⍒
Kör ⍎B Kör ett APL -uttryck U+234E ⍎
Monadiskt format ⍕B En karaktärsrepresentation av B U+2355 ⍕
Monadisk transponera ⍉B Vänd om axlarna för B U+2349 ⍉
Faktoriell !B Produkt av heltal 1 till B U+0021 !
Djup ≡B Häckningsdjup: 1 för icke-kapslad array U+2261 ≡
Tabell ⍪B Gör B till en tabell, en 2-dimensionell array. U+236A ⍪

Dyadiska funktioner

Namn Notation Menande
Unicode- kodpunkt
Lägg till A+B Summan av A och B U+002B +
Subtrahera A−B A minus B U+2212 −
Multiplicera A×B A multiplicerat med B U+00D7 ×
Dela upp A÷B A dividerat med B U+00F7 ÷
Exponentiering A⋆B A höjde till B -potentialen U+22C6 ⋆
Cirkel A○B Trigonometriska funktioner för B valda av A 
 A  =1: sin(  B  )  A  =5: sinh(  B  )  A  =2: cos(  B  )  A  =6: cosh(  B  )  A  =3: tan(  B  )  A  =7 : tanh(  B  )

Negativ producerar inversen av respektive funktioner

 U+25CB ○
Handla A?B A distinkta heltal valda slumpmässigt från de första B heltal U+003F ?
Medlemskap, Epsilon A∈B 1 för element av A som finns i B ; 0 där inte. U+2208 ∈
Hitta, Epsilon Underbar A⍷B 1 för startpunkten för multi-item array A närvarande i B ; 0 där inte. U+2377 ⍷
Max , tak A⌈B Det högre värdet av A eller B U+2308 ⌈
Minimum , Golv A⌊B Det mindre värdet på A eller B U+230A ⌊
Omforma, Dyadic Rho A⍴B Array av form A med data B U+2374 ⍴
Ta A↑B Välj de första (eller sista) A -elementen i B enligt × A U+2191 ↑
Släppa A↓B Ta bort de första (eller sista) A -elementen i B enligt × A U+2193 ↓
Avkoda A⊥B Värdet på ett polynom vars koefficienter är B vid A U+22A5 ⊥
Koda A⊤B Base- En representation av värdet på B U+22A4 ⊤
Återstod A∣B B modulo A U+2223 ∣
Catenation A,B Element av B läggs till elementen i A U+002C ,
Expansion, Dyadic Backslash A\B Infoga nollor (eller blanksteg) i B motsvarande nollor i A U+005C \
Kompression, Dyadic Slash A/B Välj element i B som motsvarar de i A U+002F /
Index av, Dyadic Iota A⍳B Platsen (index) för B i A ; 1 +⍴ A om den inte hittas U+2373 ⍳
Matrix divide, Dyadic Quad Divide A⌹B Lösning på system av linjära ekvationer , multipel regression A x = B U+2339 ⌹
Rotation A⌽B Elementen i B är roterade A -positioner U+233D ⌽
Rotation A⊖B Elementen i B roteras A -positioner längs den första axeln U+2296 ⊖
Logaritm A⍟B Logaritm av B till bas A U+235F ⍟
Dyadiskt format A⍕B Formatera B till en teckenmatris enligt A U+2355 ⍕
Allmänt införliva A⍉B Axlarna i B är ordnade efter A U+2349 ⍉
Kombinationer A!B Antal kombinationer av B som tagits A åt gången U+0021 !
Diaeresis, Dieresis, Double-Dot A¨B Över varje, eller utför varje separat; B = på dessa; A = operation att utföra eller använda (t.ex. iota) U+00A8 ¨
Mindre än A<B Jämförelse: 1 om sant, 0 om falskt U+003C <
Mindre än eller lika A≤B Jämförelse: 1 om sant, 0 om falskt U+2264 ≤
Likvärdig A=B Jämförelse: 1 om sant, 0 om falskt U+003D =
Större än eller lika med A≥B Jämförelse: 1 om sant, 0 om falskt U+2265 ≥
Större än A>B Jämförelse: 1 om sant, 0 om falskt U+003E >
Inte jämnlikt A≠B Jämförelse: 1 om sant, 0 om falskt U+2260 ≠
Eller A∨B 0 0 Boolean logik: (falskt) om både A och B = , annars 1. Alt: 1 (Sant) om A eller B = 1 (Sant) U+2228 ∨
Och A∧B Boolean logik: 1 (Sant) om både A och B = 1 , 0 (falskt) annars U+2227 ∧
Inte heller A⍱B Boolean logik: 1 om både A och B är 0, annars 0. Alt: ~∨ = inte eller U+2371 ⍱
Nand A⍲B Boolean logik: 0 om både A och B är 1, annars 1. Alt: ~∧ = inte And U+2372 ⍲
Vänster A⊣B A U+22A3 ⊣
Höger A⊢B B U+22A2 ⊢
Match A≡B 0 om A inte matchar B exakt med avseende på värde, form och kapsling; annars 1. U+2261 ≡
Laminera A⍪B Sammanfoga längs första axeln U+236A ⍪

Operatörer och axelindikator

Namn Symbol Exempel Betydelse (till exempel) Unicode kodpunktssekvens
Minska (sista axeln), snedstreck / +/B Summa över B U+002F /
Reducera (första axeln) ⌿ +⌿B Summera B U+233F ⌿
Skanna (sista axeln), snedstreck \ +\B Löpande summa över B U+005C \
Skanna (första axeln) ⍀ +⍀B Löpande summa B U+2340 ⍀
Inre produkt . A+.×B Matrisprodukt av A och B U+002E .
Yttre produkt ∘. A∘.×B Yttre produkt av A och B U+2218 ∘ , U+002E .

Anmärkningar: Operatörerna för reducering och skanning förväntar sig en dyadisk funktion till vänster, som bildar en monadisk sammansatt funktion applicerad på vektorn till höger.

Produktoperatören "." förväntar sig en dyadisk funktion till både vänster och höger, och bildar en dyadisk sammansatt funktion som appliceras på vektorerna till vänster och höger. Om funktionen till vänster om punkten är "∘" (betecknar null) så är den sammansatta funktionen en yttre produkt, annars är den en inre produkt. En inre produkt avsedd för konventionell matrismultiplikation använder funktionerna + och ×, att ersätta dessa med andra dyadiska funktioner kan resultera i användbara alternativa operationer.

Vissa funktioner kan följas av en axelindikator inom (fyrkantiga) parenteser, dvs. denna visas mellan en funktion och en array och ska inte förväxlas med array-sänkningar som skrivs efter en array. Till exempel, givet funktionen ⌽ (omvändning) och en tvådimensionell array, fungerar funktionen som standard längs den sista axeln men detta kan ändras med en axelindikator:

Som ett särskilt fall, om den dyadiska katenatfunktionen "," följs av en axelindikator (eller axelmodifierare till en symbol/funktion), kan den användas för att laminera (inskjuta) två arrayer beroende på om axelindikatorn är mindre än eller större än indexets ursprung (indexets ursprung = 1 i illustrationen nedan):

Kapslade arrayer

Matriser är strukturer som har element grupperade linjärt som vektorer eller i tabellform som matriser – och högre dimensioner (3D eller kuberad, 4D eller kuberad över tid , etc.). Matriser som innehåller både tecken och siffror kallas för blandade matriser . Arraystrukturer som innehåller element som också är arrayer kallas kapslade arrayer .

Skapa en kapslad array
Användarsession med APL-tolk Förklaring 
       
      
         
        
    
    
      

      

      
 X  ←  4  5  ⍴⍳  20  X  1  2  3  4  5  6  7  8  9  10  11  12  13  14  15  16  17  18  19  20  X  [  2  ;  2  ]  7  ⎕IO  1  X  [  1  ;  1  ]  1


X set = till matris med 4 rader gånger 5 kolumner, bestående av 20 på varandra följande heltal.

Element X[2;2] i rad 2 - kolumn 2 är för närvarande ett heltal = 7 .

Initialt index ursprung ⎕IO värde = 1 .

Således är det första elementet i matrisen X eller X[1;1] = 1 . 

      
       
      
                  
              

             
                

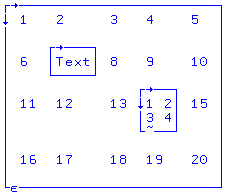
              X  [  2  ;  2  ]  ←  ⊂  "Text"  X  [  3  ;  4  ]  ←  ⊂  (  2  2  ⍴⍳  4  )  X  1  2  3  4  5  6  Text  8  9  10  11  12  13  1  2  15  3  4  16  17  18  19  20
Element i X[rad 2; kol 2] ändras (från 7) till en kapslad vektor "Text" med hjälp av funktionen omslut ⊂ .


Element i X[rad 3; kol 4], tidigare heltal 14, blir nu en miniinnesluten eller ⊂ kapslad 2x2-matris med 4 på varandra följande heltal.

Eftersom X innehåller siffror , text och kapslade element är det både en blandad och en kapslad matris.

Visuell representation av den kapslade arrayen

Flödeskontroll

En användare kan definiera anpassade funktioner som, liksom variabler, identifieras med namn snarare än med en icke-textuell symbol. Funktionshuvudet definierar om en anpassad funktion är niladisk (inga argument), monadisk (ett högerargument) eller dyadisk (vänster- och högerargument), det lokala namnet på resultatet (till vänster om tilldelningspilen ← ) och om den har några lokala variabler (var och en separerad med semikolon ';').

Användarfunktioner
Niladisk funktion PI eller π(pi) Monadisk funktion CIRCLEAREA Dyadisk funktion SEGMENTAREA, med lokala variabler 
  
   
  ∇  RESULTAT  ←  PI  RESULTAT  ←  ○  1  ∇ 

   
   
  ∇  AREA  ←  CIRCLEAREA  RADIUS  AREA  ←  PI  ×  RADIUS  ⋆  2  ∇ 

        
   
    
   
  ∇  AREA  ←  GRADER  SEGMENTAREA  RADIUS  ;  BRÖKNING  ;  CA  FRAKTION  ←  GRADER  ÷  360  CA  ←  CIRKLEARE  RADIUS  AREA  ←  BRÖK  ×  CA  ∇

Huruvida funktioner med samma identifierare men olika känslighet är distinkta är implementeringsdefinierad. Om det tillåts kan en funktion CURVEAREA definieras två gånger för att ersätta både monadiskt CIRCLEAREA och dyadiskt SEGMENTAREA ovan, där den monadiska eller dyadiska funktionen väljs av det sammanhang i vilket den refererades.

Anpassade dyadiska funktioner kan vanligtvis appliceras på parametrar med samma konventioner som inbyggda funktioner, dvs arrayer ska antingen ha samma antal element eller så ska ett av dem ha ett enda element som utökas. Det finns undantag från detta, till exempel skulle en funktion för att konvertera pre-decimal brittisk valuta till dollar förväntas ta en parameter med exakt tre element som representerar pund, shilling och pence.

Inuti ett program eller en anpassad funktion kan kontrollen villkorligt överföras till en sats som identifieras av ett radnummer eller explicit etikett; om målet är 0 (noll) avslutar detta programmet eller återgår till en funktions anropare. Den vanligaste formen använder APL-komprimeringsfunktionen, som i mallen (villkoret)/målet som har effekten att utvärdera villkoret till 0 (falskt) eller 1 (sant) och sedan använda det för att maskera målet (om villkoret är falskt ignoreras det, om det är sant lämnas det ifred så kontrollen överförs).

Därför kan funktionen SEGMENTAREA modifieras för att avbryta (precis nedan), vilket returnerar noll om parametrarna (GRADER och RADIUS nedan) har olika tecken: 

              
  
           
       
  0                      
  0                     
  
 ∇  AREA  ←  GRADER  SEGMENTAREA  RADIUS  ;  BRÖKNING  ;  CA  ;  SIGN  ⍝ lokala variabler betecknade med semikolon(;)  FRACTION  ←  GRADER  ÷  360  CA  ←  CIRCLEAREA  RADIUS  ⍝ denna APL-kodsats anropar användarfunktionen CIRCLEAREA, definierad ovan.  TECKN  ←  (  ×  GRADER  )  ≠×  RADIUS  ⍝ << APL-logik TEST/bestäm om GRADER och RADIUS INTE (≠ används) har samma TECKN 1-ja olika (≠), 0-nej (samma tecken)  AREA  ←  ⍝ standardvärde av AREA set = noll  →  TECKN  /  ⍝ förgrening (här, avslutar) inträffar när TECKN=1 medan TECKN=0 INTE förgrenar sig till 0. Förgrening till 0 avslutar funktionen.  AREA  ←  BRÅK  ×  CA  ∇

Ovanstående funktion SEGMENTAREA fungerar som förväntat om parametrarna är skalärer eller arrayer med ett element , men inte om de är arrayer med flera element eftersom villkoret i slutändan är baserat på ett enda element i SIGN-matrisen - å andra sidan, användaren funktion kan modifieras för att korrekt hantera vektoriserade argument. Operationen kan ibland vara oförutsägbar eftersom APL definierar att datorer med vektorbearbetningsförmåga ska parallelliseras och kan ordna om arrayoperationer så långt det är möjligt - testa och felsöka användarfunktioner, särskilt om de kommer att användas med vektor- eller till och med matrisargument. Detta påverkar inte bara explicit tillämpning av en anpassad funktion på arrayer, utan också dess användning överallt där en dyadisk funktion rimligen kan användas, till exempel vid generering av en resultattabell: 

                90  180  270  ¯90  ∘.  SEGMENTOMRÅDE  1  ¯2  4 
0 0 0
0 0 0
0 0 0
0 0 0

Ett mer kortfattat och ibland bättre sätt - att formulera en funktion är att undvika explicita överföringar av kontroll, istället använda uttryck som utvärderar korrekt i alla eller de förväntade förhållandena. Ibland är det korrekt att låta en funktion misslyckas när ett eller båda inmatningsargumenten är felaktiga - just för att låta användaren veta att ett eller båda argumenten som användes var felaktiga. Följande är mer kortfattat än ovanstående SEGMENTAREA-funktion. Nedanstående hanterar, vilket är viktigt, korrekt vektoriserade argument: 

          
   
    
   
     
 

               
 0           
  0           
  0           
0            ∇  AREA  ←  GRADER  SEGMENTAREA  RADIUS  ;  BRÖKNING  ;  CA  ;  TECKNBRÖKNING  ←  GRADER  ÷  360  CA  ←  CIRKLEARE  RADIUSTECKEN  ←  (  ×  GRADER  )  ≠×  RADIEOMRÅDE  ←  BRÅK  ×  CA  ×  ~  TECKN ⍝ denna APL   -  sats är mer komplex, som ett ensidigt vektoriserat argument - men det löser  :  komplexitet kontra förgrening  ∇  90  180  270  ¯90  ∘.  SEGMENTOMRÅDE  1  ¯2  4  0,785398163  12,5663706  1,57079633  25,1327412  2,35619449  37,6991118  ¯3,14159265  0

Att undvika explicita överföringar av kontroll även kallat förgrening, om den inte granskas eller kontrolleras noggrant - kan främja användningen av överdrivet komplexa one-liners , verkligen "missförstådda och komplexa idiom" och en "skrivbara" stil, som inte har gjort mycket för att göra APL till inflytelserika kommentatorer som Edsger Dijkstra . Omvänt kan dock APL-idiom vara roliga, pedagogiska och användbara - om de används med hjälpsamma kommentarer ⍝ , till exempel inklusive källa och avsedd betydelse och funktion av idiom(en). Här är en

Diverse

Diverse symboler
Namn Symbol Exempel Betydelse (till exempel) Unicode-kodpunkt
Högt minus ¯ ¯3 Betecknar ett negativt tal U+00AF ¯
Lampa, kommentar ⍝ ⍝Detta är en kommentar Allt till höger om ⍝ anger en kommentar U+235D ⍝
RightArrow, Branch, GoTo → →Denna_etikett →This_Label skickar APL-körning till This_Label: U+2192 →
Tilldela, Vänsterpil, Ange till ← B←A B←A ställer in värden och formen på B för att matcha A U+2190 ←

De flesta APL-implementeringar stöder ett antal systemvariabler och funktioner, vanligtvis föregås av tecknet ⎕ (quad) och/eller ")" ( hook =stäng parentes). Observera att fyrtecknet inte är detsamma som Unicode-symbolen för saknade tecken . Särskilt viktig och allmänt implementerad är variabeln ⎕IO ( Index Origin ), eftersom medan den ursprungliga IBM APL baserade sina arrayer på 1, baserar vissa nyare varianter dem på noll:

Användarsession med APL-tolk Beskrivning 
        
        
           
        

        
 X  ←  ⍳  12  X  1  2  3  4  5  6  7  8  9  10  11  12  ⎕IO  1  X  [  1  ]  1

X set = till vektor med 12 på varandra följande heltal.

Initialt index ursprung ⎕IO värde = 1 . Således är den första positionen i vektor X eller X[1] = 1 per vektor av jotavärden { 1 2 3 4 5 ...}. 

        0
        

        0
 ⎕IO  ←  X  [  1  ]  2  X  [  ]  1
Index Ursprung ⎕IO ändras nu till 0. Således ändras den 'första indexpositionen' i vektor X från 1 till 0. Följaktligen refererar X[1] sedan till eller pekar på 2 från {1 2 3 4 5 ...} och X[0] refererar nu till 1 . 
        
 ⎕WA  41226371072
Quad WA eller ⎕WA , en annan dynamisk systemvariabel , visar hur mycket arbetsyta som förblir oanvänd eller 41 226 megabyte eller cirka 41 gigabyte oanvänd ytterligare total ledig arbetsyta tillgänglig för APL-arbetsytan och programmet att bearbeta med. Om denna siffra blir låg eller närmar sig noll - kan datorn behöva mer RAM -minne (Random Access Memory ), hårddiskutrymme eller någon kombination av de två för att öka det virtuella minnet . 
        
 )  VARS  X
)VARS en systemfunktion i APL, )VARS visar användarvariabelnamn som finns i den aktuella arbetsytan.

Det finns också systemfunktioner tillgängliga för användare för att spara den aktuella arbetsytan, t.ex. )SAVE och avsluta APL-miljön, t.ex. ) OFF - ibland kallade hook- kommandon eller funktioner på grund av användningen av en ledande högerparentes eller hook. Det finns en viss standardisering av dessa quad- och krokfunktioner.

Teckensnitt

Unicode Basic Multilingual Plane inkluderar APL-symbolerna i blocket Diverse tekniska , som därför vanligtvis återges korrekt från de större Unicode-teckensnitten installerade med de flesta moderna operativsystem. Dessa typsnitt är sällan designade av typografer som är bekanta med APL-glyfer. Så även om de är korrekta kan glyferna se obekanta ut för APL-programmerare eller vara svåra att skilja från varandra.

Vissa Unicode-teckensnitt har designats för att visa APL väl: APLX Upright, APL385 Unicode och SimPL.

Innan Unicode försågs APL-tolkarna med typsnitt där APL-tecken mappades till mindre vanliga positioner i ASCII-teckenuppsättningarna, vanligtvis i de övre 128 kodpunkterna. Dessa mappningar (och deras nationella varianter) var ibland unika för varje APL-leverantörs tolk, vilket gjorde visningen av APL-program på webben, i textfiler och manualer - ofta problematisk.

APL2 tangentbordsfunktion till symbolmappning

APL2 Keyboard
APL2 tangentbord

Notera APL På/Av-tangenten - tangenten längst upp till höger, precis nedanför. Notera också att tangentbordet hade cirka 55 unika (68 listade per tabell ovan, inklusive jämförande symboler men flera symboler förekommer i både monadiska och dyadiska tabeller) APL-symbolnycklar (55 APL-funktioner (operatörer) är listade i IBMs 5110 APL Reference Manual), alltså med användning av alt-, skift- och ctrl-tangenter - det skulle teoretiskt sett ha tillåtit maximalt cirka 59 (tangenter) *4 (med 2-tangenter) *3 (med tre-tangenter, t.ex. ctrl-alt-del) eller cirka 472 olika maximala tangentkombinationer, närmar sig 512 EBCDIC -teckenmax (256 tecken gånger 2 koder för varje tangentkombination). Återigen, i teorin skulle tangentbordet på bilden här ha tillåtit cirka 472 olika APL-symboler/funktioner att vara tangentbordsinmatning, aktivt använda. I praktiken använde tidiga versioner bara något som ungefär motsvarar 55 APL specialsymboler (exklusive bokstäver, siffror, skiljetecken, etc. nycklar). Sålunda använde tidig APL då endast cirka 11 % (55/472) av ett symboliskt språks vid den tidpunkten användningspotential, baserat på gränser för # tangenter på tangentbordet, återigen exklusive siffror, bokstäver, skiljetecken, etc. I en annan mening tangentbordssymboler utnyttjandet var närmare 100 %, mycket effektivt, eftersom EBCDIC endast tillät 256 distinkta tecken och ASCII endast 128.

Lösa pussel

APL har visat sig vara extremt användbar för att lösa matematiska pussel, av vilka flera beskrivs nedan.

Pascals triangel

Ta Pascals triangel , som är en triangulär array av tal där de i ändarna av raderna är 1 och vart och ett av de andra talen är summan av de två närmaste talen i raden precis ovanför den (spetsen, 1, är vid toppen). Följande är en APL one-liner-funktion för att visuellt avbilda Pascals triangel: 

      00   
                                   
                                            
                                           
                                          
                                         
                                      
                                    
                                   Pascal  ←  {  ~  ¨⍨  a  ⌽⊃⌽∊  ¨  ,  ¨¨  a  ∘  !  ¨  a  ←  ⌽⍳  ⍵  }  ⍝ Skapa en enrads användarfunktion som heter Pascal  Pascal  7 ⍝   Kör  funktionen Pascal för sju rader och visa resultaten nedan:  1  1  2 1  3  3  1  4  6  4  1  5  10  10  5  1  2  0 6  15  15  6  1  7  21  35  35  21  7

Primtal, motbevis via faktorer

Bestäm antalet primtal (primtal är ett naturligt tal större än 1 som inte har några positiva divisorer förutom 1 och sig själv) upp till något tal N. Ken Iverson krediteras med följande enradiga APL-lösning på problemet: 

         
      
0  
           
                        
       
                        ⎕CR  'PrimeNumbers'  ⍝ Visa APL-användarfunktion PrimeNumbers  Primes  ←  PrimeNumbers  N  ⍝ Funktionen tar en höger arg N (t.ex. visa primtal för 1 ... int N)  Primes  ←  (  2  =+  ⌿  =  (  ⍳  N  )  ) ∘ |  ⍳  N  )  /  ⍳  N  ⍝ Ken Iverson one-liner  PrimeNumbers  100  ⍝  Visa alla primtal från 1 till 100  2  3  5  7  11  13  17  19  23  29  31  37  41  43  57  7  7  7  41  43  57  7  89  97  ⍴  Primtal  100  25  ⍝ Det finns tjugofem primtal i intervallet upp till 100.

Att undersöka motsatsen eller motsatsen till en matematisk lösning behövs ofta ( heltalsfaktorer av ett tal ): Bevisa för delmängden av heltal från 1 till 15 att de är icke-primtal genom att lista deras nedbrytningsfaktorer . Vilka är deras icke-en-faktorer (# är delbart med, förutom 1)? 

       
 


0  
   
0               
  
0  
   

             
      
      
      
           
      
            
      
            
           
            
      
              
      
            
            ⎕CR  'ProveNonPrime'  Z  ←  ProveNonPrime  R  ⍝Visa alla faktorer för ett heltal R - utom 1 och själva talet,  ⍝ dvs bevisa Icke-Prime. Strängen 'prime' returneras för ett primtal heltal.   Z  ←  (  =  (  ⍳  R  )  |  R  )  /  ⍳  R  ⍝ Bestäm alla faktorer för heltal R, lagra i Z  Z  ←  (  ~  (  Z  ∊  1  ,  R  ))  /  Z  ⍝ Ta bort 1 och talet som faktorer för talet från Z.  →  (  =⍴  Z  )  /  ProveNonPrimeIsPrime  ⍝ Om resultatet har nollform, har det inga andra faktorer och är därför primtal  Z  ←  R  ,  (  ⊂  " factors(except 1) "  )  ,  (  ⊂  Z  )  ,  ⎕TCNL  ⍝ Visa talet R, dess faktorer (förutom 1, sig själv), och en ny linje char  →  ⍝ Klar med funktion om icke-primtal  ProveNonPrimeIsPrime  :  Z  ←  R  ,  (  ⊂  "primtal"  )  ,  ⎕TCNL  ⍝ funktion förgrenas här om numret var primtal  ProveNonPrime  ¨  ⍳  15  ⍝ Bevisa icke-primtal för varje(¨) av heltal från 1 till 15 (  iota  15  )  1  primtal  2  primtal  3  primtal  4  faktorer  (  utom  1  )  2  5  primtal  6  faktorer  (  utom  3  7  )  8  faktorer  (  utom  1  )  2  4  9  faktorer  (  utom  1  )  3  10  faktorer  (  utom  1  )  2  5  11  primtal  12  faktorer  (  utom  1  )  2  3  4  6  13  primtal  14  faktorer  (  utom  1  )  2  7  utom  15  faktorer  _  _  )  3  5

Fibonacci-sekvens

Generera en Fibonacci-nummersekvens , där varje efterföljande nummer i sekvensen är summan av de två föregående: 

                     
    

  0  0     0     

          
0                 ⎕CR  'Fibonacci'  ⍝ Displayfunktion Fibonacci  FibonacciNum  ←  Fibonacci  Nth  ;  IOwas  ⍝ Funktionshuvud, funktionsnamn=Fibonacci, monadisk funktion med 1 högerhands arg Nth;local var IOwas, och ett returnerat num.  ⍝Generera ett Fibonacci-sekvensnummer där Nth är positionen # för Fibonacci-numret i sekvensen. << funktionsbeskrivning   IOvar  ←  ⎕IO  ⋄  ⎕IO  ←  ⋄  FibonacciNum  ←  ↑  1  ↓↑+  .  ×  /  Nth  /  ⊂  2  2  ⍴  1  1  1  ⋄  ⎕IO  ←  IOwas  ⍝ För att denna funktion ska fungera korrekt måste ⎕IO vara inställd på noll.  Fibonacci  ¨  ⍳  14  ⍝ Denna APL-sats säger: Generera Fibonacci-sekvensen över varje (¨) heltal (iota eller ⍳) för heltal 1..14.  1  1  2  3  5  8  13  21  34  55  89  144  233  ⍝ Genererad sekvens, dvs Fibonacci-nummersekvensen genererad av APL:s tolk.

Vidare läsning

  •   Polivka, Raymond P.; Pakin, Sandra (1975). APL: Språket och dess användning . Prentice-Hall. ISBN 978-0-13-038885-8 .
  •   Reiter, Clifford A.; Jones, William R. (1990). APL med matematisk accent (1 uppl.). Taylor och Francis. ISBN 978-0534128647 .
  •   Thompson, Norman D.; Polivka, Raymond P. (2013). APL2 in Depth (Springer Series in Statistics) (Paperback) (Reprint av originalet 1:a upplagan). Springer. ISBN 978-0387942131 .
  •   Gilman, Leonard; Rose, Allen J. (1976). APL: An Interactive Approach (Paperback) (3:e upplagan). ISBN 978-0471093046 .

Se även

externa länkar

Generiska online tutorials

Syntaxregler

Hämtad från " https://en.wikipedia.org/w/index.php?title=APL_syntax_and_symbols&oldid=1136216278 "