Vik (högre ordningsfunktion)
I funktionell programmering avser fold (även kallat reducera , ackumulera , aggregera , komprimera eller injicera ) en familj av högre ordningens funktioner som analyserar en rekursiv datastruktur och genom användning av en given kombinationsoperation, rekombinerar resultaten av rekursiv bearbetning av dess beståndsdelar, bygga upp ett returvärde. Vanligtvis presenteras en fold med en kombinerande funktion , en toppnod i en datastruktur och möjligen några standardvärden som ska användas under vissa förhållanden. Viken fortsätter sedan med att kombinera delar av datastrukturens hierarki , med hjälp av funktionen på ett systematiskt sätt.
Vikningar är på sätt och vis dubbla till unfolds , som tar ett startvärde och tillämpar en funktion corecursively för att bestämma hur en corecursive datastruktur ska konstrueras, medan en fold rekursivt bryter ner den strukturen och ersätter den med resultatet av att tillämpa en kombinerande funktion vid varje nod på sina terminalvärden och de rekursiva resultaten ( katamorfism , kontra anamorfism av utveckningar).
Som strukturella omvandlingar
Vikningar kan ses som att de konsekvent ersätter de strukturella komponenterna i en datastruktur med funktioner och värden. Listor , till exempel, är uppbyggda i många funktionella språk från två primitiver: vilken lista som helst är antingen en tom lista, vanligen kallad noll ( [] ), eller är konstruerad genom att prefixet ett element framför en annan lista, skapar vad som kallas en cons node ( Cons(X1,Cons(X2,Cons(...(Cons(Xn,nil))))) ), som härrör från tillämpningen av en cons -funktion (skriven ned som ett kolon (:) i Haskell ). Man kan se en vikning på listor som att ersätta noll i slutet av listan med ett specifikt värde och ersätta varje nackdel med en specifik funktion . Dessa ersättningar kan ses som ett diagram:
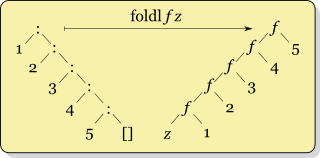
Det finns ett annat sätt att utföra den strukturella transformationen på ett konsekvent sätt, med ordningen för de två länkarna i varje nod vänd när de matas in i kombinationsfunktionen:
Dessa bilder illustrerar höger och vänster veck av en lista visuellt. De lyfter också fram det faktum att foldr (:) [] är identitetsfunktionen på listor (en ytlig kopia på Lisp -språk), eftersom att ersätta nackdelar med nackdelar och noll med noll inte kommer att ändra resultatet. Det vänstra vikningsdiagrammet föreslår ett enkelt sätt att vända en lista, foldl (vänd (:)) [] . Observera att parametrarna till nackdelar måste vändas, eftersom elementet som ska läggas till nu är den högra parametern för kombinationsfunktionen. Ett annat enkelt resultat att se från denna utsiktspunkt är att skriva kartfunktionen av högre ordning i termer av foldr , genom att komponera funktionen för att agera på elementen med nackdelar , som:
map f = foldr (( : ) . f ) []
där perioden (.) är en operator som anger funktionssammansättning .
Det här sättet att se på saker ger en enkel väg till att designa veckliknande funktioner på andra algebraiska datatyper och strukturer, som olika sorters träd. Man skriver en funktion som rekursivt ersätter datatypens konstruktörer med tillhandahållna funktioner och eventuella konstanta värden av typen med tillhandahållna värden. En sådan funktion kallas i allmänhet för en katamorfism .
På listor
Vikningen av listan [1,2,3,4,5] med additionsoperatorn skulle resultera i 15, summan av elementen i listan [ 1,2,3,4,5] . Till en grov uppskattning kan man tänka sig denna veckning som att ersätta kommatecken i listan med operationen +, vilket ger 1 + 2 + 3 + 4 + 5 .
I exemplet ovan är + en associativ operation , så slutresultatet blir detsamma oavsett parentes, även om det specifika sättet på vilket det beräknas kommer att vara annorlunda. I det allmänna fallet med icke-associativa binära funktioner kan ordningen i vilken elementen kombineras påverka det slutliga resultatets värde. På listor finns det två uppenbara sätt att utföra detta: antingen genom att kombinera det första elementet med resultatet av att rekursivt kombinera resten (kallad en högervikning ), eller genom att kombinera resultatet av att rekursivt kombinera alla element utom det sista, med det sista elementet (kallas en vänstervikning ). Detta motsvarar att en binär operator är antingen högerassociativ eller vänsterassociativ, i Haskells eller Prologs terminologi. Med en högervikning skulle summan inordnas inom parentes som 1 + (2 + (3 + (4 + 5))) , medan den med en vänstervikning skulle sättas inom parentes som (((1 + 2) + 3) + 4) + 5 .
I praktiken är det bekvämt och naturligt att ha ett startvärde som vid högervikning används när man når slutet av listan, och vid vänstervikning är det som initialt kombineras med det första elementet av listan. I exemplet ovan skulle värdet 0 (den additiva identiteten ) väljas som ett initialt värde, vilket ger 1 + (2 + (3 + (4 + (5 + 0)))) för den högra veckningen, och ((( (0 + 1) + 2) + 3) + 4) + 5 för vänster veck. För multiplikation skulle ett initialt val av 0 inte fungera: 0 * 1 * 2 * 3 * 4 * 5 = 0 . Identitetselementet för multiplikation är 1. Detta skulle ge oss utfallet 1 * 1 * 2 * 3 * 4 * 5 = 120 = 5! .
Linjära kontra trädliknande veck
Användningen av ett initialvärde är nödvändigt när kombinationsfunktionen f är asymmetrisk i sina typer (t.ex. a → b → b ), dvs när typen av dess resultat skiljer sig från typen av listans element. Då måste ett initialvärde användas, med samma typ som f :s resultat, för att en linjär kedja av tillämpningar ska vara möjlig. Om det kommer att vara vänster- eller högerorienterat kommer att bestämmas av de typer som förväntas av dess argument av den kombinerande funktionen. Om det är det andra argumentet som måste vara av samma typ som resultatet, f ses som en binär operation som associerar till höger och vice versa.
När funktionen är en magma , dvs symmetrisk i sina typer ( a → a → a ), och resultattypen är densamma som listelementens typ, kan parentesen placeras på godtyckligt sätt och skapa ett binärt träd av kapslade sub -uttryck, t.ex. ((1 + 2) + (3 + 4)) + 5 . Om den binära operationen f är associativ kommer detta värde att vara väldefinierat, dvs samma för alla parenteser, även om operationsdetaljerna för hur det beräknas kommer att vara olika. Detta kan ha betydande inverkan på effektiviteten om f är icke-strikt .
Medan linjära veck är nodorienterade och fungerar på ett konsekvent sätt för varje nod i en lista , är trädliknande veck hellistorienterade och fungerar på ett konsekvent sätt över grupper av noder.
Särskilda veck för icke-tomma listor
Man vill ofta välja identitetselementet för operationen f som initialvärde z . När inget initialvärde verkar lämpligt, till exempel när man vill vika funktionen som beräknar det maximala av dess två parametrar över en icke-tom lista för att få det maximala elementet i listan, finns det varianter av foldr och foldl som använder sista och första elementet i listan som startvärde. På Haskell och flera andra språk kallas dessa foldr1 och foldl1 , 1:an hänvisar till den automatiska tillhandahållandet av ett initialt element, och det faktum att listorna de tillämpas på måste ha minst ett element.
Dessa veck använder typsymmetrisk binär operation: typen av både dess argument och dess resultat måste vara desamma. Richard Bird i sin bok från 2010 föreslår "en allmän vikningsfunktion på icke-tomma listor" foldrn som omvandlar sitt sista element, genom att applicera en extra argumentfunktion på den, till ett värde av resultattypen innan själva veckningen påbörjas, och är således kunna använda typasymmetrisk binär operation som den vanliga mappen för att producera ett resultat av typ som skiljer sig från listans elementtyp.
Genomförande
Linjära veck
Med Haskell som exempel kan foldl och foldr formuleras i några få ekvationer.
foldl :: ( b -> a -> b ) -> b -> [ a ] -> b foldl f z [] = z foldl f z ( x : xs ) = foldl f ( f z x ) xs
Om listan är tom är resultatet startvärdet. Om inte, vik listans svans och använd som nytt initialvärde resultatet av att tillämpa f på det gamla initiala värdet och det första elementet.
foldr :: ( a -> b -> b ) -> b -> [ a ] -> b foldr f z [] = z foldr f z ( x : xs ) = f x ( foldr f z xs )
Om listan är tom är resultatet det initiala värdet z. Om inte, applicera f på det första elementet och resultatet av att vika resten.
Trädliknande veck
Listor kan vikas över på ett trädliknande sätt, både för ändliga och för obestämda listor:
foldt f z [] = z foldt f z [ x ] = f x z foldt f z xs = foldt f z ( par f xs ) foldi f z [ ] = z foldi f z ( x : xs ) = f x ( foldi f z ( par f xs )) par f ( x : y : t ) = f x y : par f t par _ t = t
När det gäller foldi -funktionen, för att undvika dess skenande utvärdering på obestämda listor, får funktionen f inte alltid kräva sitt andra arguments värde, åtminstone inte allt, eller inte omedelbart (se exempel nedan).
Fälls för icke-tomma listor
foldl1 f [ x ] = x foldl1 f ( x : y : xs ) = foldl1 f ( f x y : xs ) foldr1 f [ x ] = x foldr1 f ( x : xs ) = f x ( foldr1 f xs ) foldt1 f [ x ] = x foldt1 f ( x : y : xs ) = foldt1 f ( f x y : par f xs ) foldi1 f [ x ] = x fold1 f ( x : xs ) = f x ( foldi1 f ( par f xs ) ))
Överväganden vid utvärderingsordning
I närvaro av lat , eller icke-strikt utvärdering, kommer foldr omedelbart att återföra tillämpningen av f till listans huvud och det rekursiva fallet att vika över resten av listan. Således, om f kan producera någon del av sitt resultat utan hänvisning till det rekursiva fallet på "höger sida", dvs. i sitt andra argument, och resten av resultatet aldrig krävs, kommer rekursionen att sluta ( t.ex. == foldr ( \ a b -> a ) ( fel "tom lista") ) . Detta gör att högervikningar kan fungera på oändliga listor. Däremot foldl omedelbart att anropa sig själv med nya parametrar tills den når slutet av listan. Denna svansrekursion kan effektivt kompileras som en loop, men kan inte hantera oändliga listor alls – den kommer att återkomma för alltid i en oändlig loop .
Efter att ha nått slutet av listan byggs ett uttryck i själva verket av en foldl av kapslade vänsterfördjupande f -applikationer, som sedan presenteras för anroparen för att utvärderas. Om funktionen f skulle referera till sitt andra argument först här och kunna producera en del av sitt resultat utan hänvisning till det rekursiva fallet (här till vänster, dvs. i sitt första argument), så skulle rekursionen sluta. Detta betyder att även om foldr återkommer till höger , tillåter den en lat kombinationsfunktion för att inspektera listans element från vänster; och omvänt, medan foldl återkommer till vänster , tillåter det en lat kombinationsfunktion för att inspektera listans element från höger, om den så väljer (t.ex. sista == foldl ( \ a b -> b ) ( fel "tom lista" ) ).
Att vända en lista är också svansrekursivt (det kan implementeras med rev = foldl ( \ ys x -> x : ys ) [] ). På finita listor betyder det att vänstervikning och reversering kan sammansättas för att utföra en högervikning på ett svansrekursivt sätt (jfr 0 0 1 +> ( 2 +> ( 3 +> )) == (( <+ 3 ) <+ 2 ) <+ 1 ), med en modifiering av funktionen f så att den vänder ordningen på sina argument (dvs foldr f z == foldl ( flip f ) z . foldl ( flip ( : )) [] ), svansrekursivt bygga en representation av uttryck som högerveckning skulle bygga. Den främmande mellanliggande liststrukturen kan elimineras med fortsättningsövergångsstilstekniken , foldr f z xs == foldl ( \ k x -> k . f x ) id xs z ; på liknande sätt, foldl f z xs == foldr ( \ x k -> k . flip f x ) id xs z ( flip behövs bara i språk som Haskell med dess vända ordning av argument till kombinationsfunktionen av foldl till skillnad från t.ex. i Scheme där samma ordning av argument används för att kombinera funktioner till både foldl och foldr ).
En annan teknisk punkt är att, i fallet med vänstervikningar med lata utvärdering, utvärderas den nya initiala parametern inte innan det rekursiva anropet görs. Detta kan leda till stackoverflows när man når slutet av listan och försöker utvärdera det resulterande potentiellt gigantiska uttrycket. Av denna anledning tillhandahåller sådana språk ofta en striktare variant av vänstervikning som tvingar fram utvärderingen av den initiala parametern innan det rekursiva anropet görs. I Haskell är detta foldl'- funktionen (observera apostrof, uttalad 'prime') i Data.List- biblioteket (man måste vara medveten om faktumet att framtvingande av ett värde byggt med en lat datakonstruktor inte kommer att tvinga dess beståndsdelar automatiskt av sig själv). I kombination med svansrekursion närmar sig sådana veck effektiviteten av slingor, vilket säkerställer konstant utrymmesdrift, när lat utvärdering av slutresultatet är omöjligt eller oönskat.
Exempel
Med hjälp av en Haskell- tolk kan de strukturella transformationer som vikningsfunktioner utför illustreras genom att konstruera en sträng:
λ > foldr ( \ x y -> concat [ "(" , x , " +" , y , ")" ]) "0" ( kartvisning [ 1 .. 13 ]) "(1+(2+(3) +(4+(5+(6+(7+(8+(9+(10+(11+(12+(13+0)))))))))))))" λ > foldl ( \ x y -> concat [ "(" , x , "+" , y , ")" ]) "0" ( kartvisa [ 1 .. 13 ]) "(((( ( (((((((( (0+1)+2)+3)+4)+5)+6)+7)+8)+9)+10)+11)+12)+13)" λ > foldt ( \ x y - > concat [ "(" , x , "+" , y , ")" ]) "0" ( kartvisning [ 1 .. 13 ]) "( ( (((1+2)+(3+4)) +((5+6)+(7+8)))+(((9+10)+(11+12))+13))+0)" λ > foldi ( \ x y - > konkat [ " (" , x , "+" , y , ")" ]) "0" ( kartvisning [ 1 .. 13 ]) " ( 1+((2+3)+(((4+5)+(6) +7))+((((8+9)+(10+11))+(12+13))+0))))"
Oändlig trädliknande veckning demonstreras t.ex. i rekursiv primtalsproduktion genom obunden sikt av Eratosthenes i Haskell :
primtal = 2 : _Y (( 3 : ) . minus [ 5 , 7 .. ] . foldi ( \ ( x : xs ) ys -> x : union xs ys ) [] . map ( \ p -> [ p * p , p * p + 2 * p .. ])) _Y g = g ( _Y g ) -- = g . g . g . g . ...
där funktionsfacket arbetar på ordnade listor på ett lokalt sätt för att effektivt ta fram sitt setförbund och minus deras uppsatta skillnad .
Ett ändligt prefix av primtal definieras kortfattat som en veckning av uppsättningsdifferensoperation över listorna med uppräknade multiplar av heltal, som
primtalTo n = foldl1 minus [[ 2 * x , 3 * x .. n ] | x <- [ 1 .. n ]]
För ändliga listor, t.ex. sammanslagningssortering (och dess sort som tar bort dubbletter, nubsort ) kan enkelt definieras med trädliknande vikning som
mergesort xs = foldt sammanfoga [] [[ x ] | x <- xs ] nubsort xs = foldt union [] [[ x ] | x <- xs ]
med funktionen slå samman en dubblettbevarande variant av union .
Funktioner huvud och sista kunde ha definierats genom vikning som
head = foldr ( \ x r -> x ) ( fel "huvud: Tom lista" ) last = foldl ( \ a x -> x ) ( fel "sista: Tom lista" )
På olika språk
| Språk | Vänster veck | Höger vik | Vänster vik utan startvärde | Högervikning utan initialvärde | Veckla ut | Anteckningar |
|---|---|---|---|---|---|---|
| APL |
func ⍨/⌽ initval , vektor
|
func / vektor , initival
|
func ⍨/⌽ vektor
|
func / vektor
|
||
| C# 3.0 |
|
|
|
|
Aggregate är en förlängningsmetod ienum är en IEnumerable<T> Likadant i alla .NET-språk |
|
| C++ |
|
|
i header <numeric> start , end , rbegin , rend are iterators func kan vara en funktionspekare eller ett funktionsobjekt
|
|||
| C++17 |
( initval op ... op pack )
|
( pack op ... op initval )
|
(... op pack )
|
( packa upp ...)
|
Fälluttryck (endast för variadiska mallar ): op är en binär operator (båda operationerna måste vara desamma, t.ex. ( std :: cout << ... << args ) ), pack är ett oexpanderat parameterpaket. |
|
| C++23 |
std::ranges::fold_left( range , initval , func )
|
std::ranges::fold_right( range , initval , func )
|
std::ranges::fold_left_first( range , func )
|
std::ranges::fold_right_last( range , func )
|
Både std::ranges::fold_left_first och std::ranges::fold_right_last returnerar std::valfritt med tanke på tomheten i intervallet . |
|
| CFML |
obj.reduce(func,initial)
|
obj.reduce(func)
|
Där func tar emot som argument resultatet av föregående operation (eller det initiala värdet på den första iterationen); det aktuella objektet; det aktuella objektets index eller nyckel; och en hänvisning till obj
|
|||
| Clojure |
(minska func initval lista )
|
(minska func initval (omvänd lista ))
|
( minska funktionslistan )
|
(minska funktion (omvänd lista ))
|
Se även clojure.core.reducers/fold | |
| Vanlig Lisp |
(minska funktionslistan :initial- value initval )
|
(minska funktionslistan :från-änden t :initial- värde initval )
|
( minska funktionslistan )
|
(minska funktionslistan :från slutet t )
|
||
| Ringla |
{{TreeNode. default treeNode ...} .to-Iterator }
|
{{TreeNode. default treeNode ...}
|
{för {treeNode
|
{för {{treeNode.reverse}
|
även DefaultListModel och HashTable implementerar till Iterator
|
|
| D |
minska! func ( initval , lista )
|
|
minska! func ( lista )
|
|
i modul std.algorithm
|
|
| Elixir |
List.foldl(lista, acc, kul)
|
List.foldr(lista, acc, kul)
|
Se dokumentation för till exempel användning | |||
| Alm |
List.foldl( Fun , Accumulator , List )
|
List.foldr( Fun , Accumulator , List )
|
Se även List API [1] | |||
| Erlang |
lists:foldl( Fun , Accumulator , List )
|
lists:foldr( Fun , Accumulator , List )
|
||||
| F# |
Seq/List.fold func initval lista
|
List.foldBack func list initival
|
Seq/List.reduce func list
|
List.reduceBack func list
|
Seq.unfold func initval
|
|
| Gosu |
|
Alla är förlängningsmetoder på Javas Iterable-gränssnitt, arrayer stöds också | ||||
| Häftig |
|
|
|
|
||
| Haskell |
foldl func initval lista
|
foldr func initval lista
|
foldl1 funktionslista _
|
foldr1 funktionslista _
|
unfoldr func initval
|
För foldl tar foldningsfunktionen argument i motsatt ordning som för foldr. |
| Haxe |
Lambda.fold( iterable , func , initval )
|
|||||
| J |
verb ~/|. initval , array
|
verb / array , initval
|
verb ~/|. array
|
verb / array
|
u/y tillämpar dyaden u mellan objekten i y. "J Dictionary: Infoga" | |
| Java 8+ |
|
|
||||
|
JavaScript 1.8 ECMAScript 5 |
|
|
||||
| Julia |
foldl( op , itr ; [init])
|
foldr( op , itr ; [init])
|
foldl( op , itr )
|
foldr( op , itr )
|
||
| Kotlin |
|
|
Iterable .reduce (func )
|
Iterable .reduceRight (func )
|
Andra samlingar stöder också vikning och reducering . Det finns också Result.fold(onSuccess, onFailure) , som reducerar ett Result<T> (antingen framgång eller misslyckande) till returtypen onSuccess och onFailure . |
|
| LFE |
(listor:foldl func accum list )
|
(listor:foldr func accum list )
|
||||
| Logtalk |
fold_left(Stängning, Initial, Lista, Resultat)
|
fold_right(Stängning, Initial, Lista, Resultat)
|
Meta-predikat tillhandahållna av meta -standardbiblioteksobjektet. Förkortningarna foldl och foldr kan också användas. | |||
| Lönn |
foldl( func , initval , sekvens )
|
foldr( func , initval , sekvens )
|
||||
| Mathematica |
Vik[ func , initval , list ]
|
Vik[ func , initval , Reverse[ list ]]
|
Vik[ func , list ]
|
Vik[ func , Reverse[ list ]]
|
NestWhileList[ func, , initval , predikat ]
|
Vikning utan ett initialt värde stöds i version 10.0 och högre. |
| MATLAB |
fold(@ func , list , defaultVal )
|
fold(@ func , flip( list ), defaultVal )
|
fold(@ func , lista )
|
fold(@ func , flip( lista ))
|
|
Kräver Symbolic Math Toolbox, stöds från R2016b. |
| Maxima |
lreduce( func , list , initval )
|
rreduce( func , list , initval )
|
lreduce( func , list )
|
rreduce( func , list )
|
||
| Mythryl |
|
|
Den medföljande funktionen tar sina argument i en tupel. | |||
| OCaml |
|
|
Base.Sequence.unfold ~init ~f
|
|||
| Uns |
{FoldL List Func InitVal }
|
{FoldR List Func InitVal }
|
||||
| PARI/GP |
vika ( f , A )
|
|||||
| Perl |
reducera block initval , lista
|
minska blockeringslistan _
|
i List::Util- modulen |
|||
| PHP |
array_reduce( array , func , initval )
|
|
array_reduce( array , func )
|
|
När initval inte tillhandahålls används NULL, så detta är inte en sann foldl1. Före PHP 5.3 initval bara vara heltal. "func" är en återuppringning . Prova array_reduce online. | |
| Python 2.x |
reducera( func , list , initval )
|
reducera(lambda x,y: func (y,x), reversed( list ), initval )
|
reducera( func , list )
|
reducera(lambda x,y: func (y,x), reversed( lista ))
|
||
| Python 3.x |
functools.reduce( func , list , initval )
|
functools.reduce(lambda x,y: func (y,x), reversed( list ), initval )
|
functools.reduce( func , list )
|
functools.reduce(lambda x,y: func (y,x), reversed( list ))
|
I modulens funktionsverktyg . | |
| R |
Reduce( func , list , initval )
|
Reduce( func , list , initval , right=TRUE)
|
Reduce( func , list )
|
Reduce( func , list , right=TRUE)
|
R stöder högervikning och vänster- eller högervikning med eller utan ett initialt värde genom höger- och init -argumenten till Reduce-funktionen. | |
| Rubin |
|
|
|
|
I Ruby 1.8.7+ kan även skicka en symbol som representerar en funktion istället för ett block. enum är en uppräkning Observera att dessa implementeringar av högervikningar är felaktiga för icke-kommutativa &block (även initialvärdet sätts på fel sida). |
|
| Rost |
iterator .fold( initval , func )
|
iterator .rev().fold( initval , func )
|
iterator .rev() kräver att iterator är en DoubleEndedIterator . |
|||
| Scala |
list .foldLeft( initval )( func ) ( initval /: list )( func )
|
list .foldRight( initval )( func ) ( list :\ initval )( func )
|
list .reduceLeft( func )
|
list .reduceRight( func )
|
Scalas symboliska vecksyntax var avsedd att likna det vänster- eller högerlutande träd som vanligtvis används för att förklara veckoperationen, men har sedan dess omtolkats som en illustration av en vältande domino. Kolon kommer från en allmän Scala-syntaxmekanism där den skenbara infixoperatorn anropas som en metod på vänster operand med den högra operanden skickad som ett argument, eller vice versa om operatorns sista tecken är ett kolon, här applicerat symmetriskt. Scala har också trädliknande veck med metoden |
|
| Schema R 6 RS |
|
|
(minska-vänster funktion standardval lista )
|
(minska-höger funktion standardval lista )
|
(vika ut p f g frö [svans-gen] ) veckla ut-höger p f g frö [svans] (vektor-utvikt f längd initial-frö ··· ) (vektor-uppveckning-höger f längd initial-frö ··· )
|
srfi/1 srfi/43 |
| Småprat |
aCollection inject: aValue into: aBlock
|
aCollection reduce: aBlock
|
ANSI Smalltalk definierar inte #reduce: men många implementeringar gör det. | |||
| Standard ML |
|
|
Den medföljande funktionen tar sina argument i en tupel. För foldl tar foldningsfunktionen argument i samma ordning som för foldr. | |||
| Snabb |
|
|
||||
| XPath 3.1 |
array:fold-left ( $ array som array ( *) , $ noll som objekt () * , $ f som funktion ( objekt () * , objekt () * } som objekt( ) * ) som objekt () *
fn:fold-left ( $ seq som objekt () * , $ noll som objekt () * , $ f som funktion ( objekt () * , objekt () ) som objekt () * ) som objekt () *
|
array:fold-right ( $ array som array ( *) , $ noll som objekt () * , $ f som funktion ( objekt () * , objekt () * } som objekt( ) * ) som objekt () *
fn:fold-right ( $ seq som objekt () * , $ noll som objekt () * , $ f som funktion ( objekt ( ), objekt () * ) som objekt () * ) som objekt () *
|
I XPath 3.1 på grund av historiska skäl är array- och sekvenstyperna inkompatibla - sålunda behovet av separata vikningsfunktioner för array och för sekvens
|
|||
| Xtend |
iterable .fold( initval ,[ func ])
|
iterable .reduce[ func ]
|
Universalitet
Vik är en polymorf funktion. För alla g som har en definition
g [] = v g ( x : xs ) = f x ( g xs )
då kan g uttryckas som
g = foldr f v
Dessutom, på ett lat språk med oändliga listor, kan en fixpunktskombinator implementeras via fold, vilket bevisar att iterationer kan reduceras till veck:
y f = foldr ( \ _ -> f ) odefinierad ( upprepa odefinierad )
Se även
- Aggregerad funktion
- Itererad binär operation
- Katamorfism , en generalisering av veck
- Homomorfism
- Karta (funktion med högre ordning)
- Prefix summa
- Rekursiv datatyp
- Reduktionsoperatör
- Strukturell rekursion