Tom gitter approximation

Den tomma gitterapproximationen är en teoretisk elektronisk bandstrukturmodell där potentialen är periodisk och svag (nära konstant). Man kan också överväga ett tomt ^{[ förtydligande behövs ]} oregelbundet gitter, där potentialen inte ens är periodisk. Den tomma gitterapproximationen beskriver ett antal egenskaper hos energispridningsförhållanden för icke-interagerande fria elektroner som rör sig genom ett kristallgitter . Energin hos elektronerna i det "tomma gittret" är densamma som energin för fria elektroner. Modellen är användbar eftersom den tydligt illustrerar ett antal av de ibland mycket komplexa egenskaperna hos energispridningsförhållanden i fasta ämnen som är grundläggande för alla elektroniska bandstrukturer.

Spridning och periodicitet

Fria elektronband i ett endimensionellt gitter

Den periodiska potentialen för gittret i denna fria elektronmodell måste vara svag eftersom elektronerna annars inte skulle vara fria. Styrkan på spridningen beror främst på systemets geometri och topologi. , som spridningstvärsnitt , beror på potentialens storlek och storleken på den potentiella brunnen . För 1-, 2- och 3-dimensionella utrymmen sprider potentiella brunnar alltid vågor, oavsett hur små potentialerna är, vilka tecken de har eller hur begränsade deras storlekar är. För en partikel i ett endimensionellt gitter, som Kronig–Penney-modellen , är det möjligt att beräkna bandstrukturen analytiskt genom att ersätta värdena för potentialen, gitteravståndet och storleken på potentiell brunn. För två- och tredimensionella problem är det svårare att exakt beräkna en bandstruktur baserat på en liknande modell med några få parametrar. Icke desto mindre kan egenskaperna hos bandstrukturen lätt uppskattas i de flesta regioner genom störningsmetoder .

I teorin är gittret oändligt stort, så en svag periodisk spridningspotential kommer så småningom att vara tillräckligt stark för att reflektera vågen. Spridningsprocessen resulterar i de välkända Bragg-reflektionerna av elektroner genom den periodiska potentialen hos kristallstrukturen . Detta är ursprunget till periodiciteten för spridningsrelationen och uppdelningen av k-rymden i Brillouin-zoner. Det periodiska energispridningsförhållandet uttrycks som:

E_{n}(\mathbf {k} )={\frac {\hbar ^{2}(\mathbf {k} +\ mathbf {G} _{n})^{2}}{2m}}

G $\mathbf {G} _{n}$ är de reciproka gittervektorerna till vilka banden ^{[ behövs ]} $E_{n}(\mathbf {k} )$ tillhör .

Figuren till höger visar spridningsförhållandet under tre perioder i reciprokt utrymme för ett endimensionellt gitter med gitterceller med längden a .

Energibanden och tillståndens täthet

I ett endimensionellt gitter begränsas antalet reciproka gittervektorer $\mathbf {G} _{n}$ som bestämmer banden i ett energiintervall till två när energin stiger. I två- och tredimensionella gitter ökar antalet reciproka gittervektorer som bestämmer de fria elektronbanden $E_{n}(\mathbf {k} )$ snabbare när längden på vågvektorn ökar och energin stiger. Detta beror på att antalet reciproka gittervektorer $\mathbf {G} _{n}$ som ligger i ett intervall $[\mathbf {k} ,\mathbf { k} +d\mathbf {k} ]$ ökar. Tätheten av tillstånd i ett energiintervall $[E,E+dE]$ beror på antalet tillstånd i ett intervall $[\mathbf {k} ,\mathbf {k} +d\mathbf {k} ]$ i ömsesidigt mellanrum och lutningen för spridningsrelationen $E_{n}(\mathbf {k} )$ .

Figur 3: Fri-elektron DOS i 3-dimensionell k-rymd

Även om gittercellerna inte är sfäriskt symmetriska, har spridningsrelationen fortfarande sfärisk symmetri ur synvinkeln av en fast central punkt i en reciprok gittercell om spridningsrelationen sträcker sig utanför den centrala Brillouin-zonen. Tillståndstätheten i ett tredimensionellt gitter kommer att vara densamma som i fallet med frånvaro av ett gitter . För det tredimensionella fallet är densiteten för tillstånden ${\displaystyle D_{3}\left(E\right)};$

D_{3}\left(E\right)=2\pi {\sqrt {\frac {E-E_{0}}{c_{k}^{3}}}}\ .

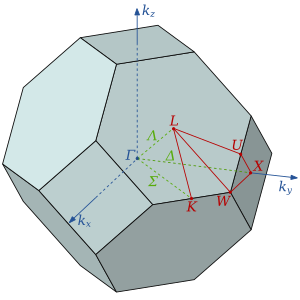
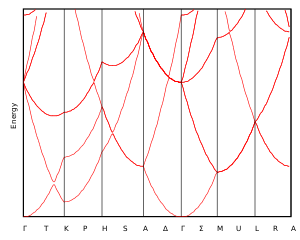
I det tredimensionella rymden är Brillouin-zonens gränser plan. Dispersionsrelationerna visar konikerna för frielektronenergidispersionsparabolerna för alla möjliga reciproka gittervektorer. Detta resulterar i en mycket komplicerad uppsättning korsning av kurvor när spridningsrelationerna beräknas eftersom det finns ett stort antal möjliga vinklar mellan utvärderingsbanor, första och högre ordningens Brillouin-zongränser och dispersionsparabolkorsningskoner.

Andra, tredje och högre Brillouin-zoner

FCC Brillouin-zon

"Fria elektroner" som rör sig genom gittret av ett fast ämne med vågvektorer $\mathbf {k}$ långt utanför den första Brillouin-zonen reflekteras fortfarande tillbaka in i den första Brillouin-zonen. Se med externa länkar för webbplatser med exempel och figurer.

Den nästan fria elektronmodellen

I de flesta enkla metaller , som aluminium , minskar skärmningseffekten kraftigt det elektriska fältet hos jonerna i det fasta ämnet. Den elektrostatiska potentialen uttrycks som

V(r)={\frac {Ze}{r}}e^{-qr}

där Z är atomnumret , e är den elementära enhetsladdningen, r är avståndet till kärnan av den inbäddade jonen och q är en screeningsparameter som bestämmer potentialens intervall. Fouriertransformen , $U_{\mathbf {G} }$ , av gitterpotentialen, V $\displaystyle V(\mathbf {r} )}$ , uttrycks som

U_{\mathbf {G} }={\frac {4\pi Ze}{q^{2}+G^{2}}}

När värdena för de off-diagonala elementen $U_{\mathbf {G} }$ mellan de reciproka gittervektorerna i Hamiltonian nästan går till noll. Som ett resultat, storleken på bandgapet $2|U_{\mathbf {G} }|$ kollapsar och den tomma gitterapproximationen erhålls.

Elektronbanden i vanliga metallkristaller

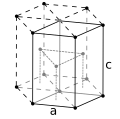
Bortsett från några exotiska undantag kristalliseras metaller i tre typer av kristallstrukturer: BCC- och FCC- kubiska kristallstrukturer och den hexagonala tätpackade HCP -kristallstrukturen.