Tutte graf
| Tutte graf | |
|---|---|
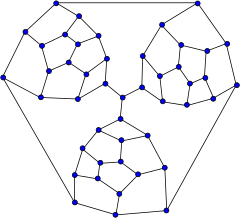 Tutte graf
| |
| Döpt efter | WT Tutte |
| Vertices | 46 |
| Kanter | 69 |
| Radie | 5 |
| Diameter | 8 |
| Omkrets | 4 |
| Automorfismer | 3 ( Z /3 Z ) |
| Kromatiskt nummer | 3 |
| Kromatiskt index | 3 |
| Egenskaper |
Kubisk plan polyedral |
| Tabell över grafer och parametrar | |
Inom det matematiska området grafteori är Tutte-grafen en 3- regelbunden graf med 46 hörn och 69 kanter uppkallad efter WT Tutte . Den har kromatiskt nummer 3, kromatiskt index 3, omkrets 4 och diameter 8.
Tutte-grafen är en kubisk polyedrisk graf , men är icke- hamiltonisk . Därför är det ett motexempel till Taits gissning att varje 3-regelbunden polyeder har en Hamiltonsk cykel.
Publicerad av Tutte 1946, det är det första motexemplet som konstruerats för denna gissning. Andra motexempel hittades senare, i många fall baserade på Grinbergs teorem .
Konstruktion
Från en liten plan graf som kallas Tutte-fragmentet, konstruerade WT Tutte en icke-Hamiltonisk polyeder genom att sätta ihop tre sådana fragment. De "obligatoriska" kanterna på fragmenten, som måste vara en del av någon Hamiltonsk väg genom fragmentet, är anslutna vid den centrala vertexen; eftersom varje cykel bara kan använda två av dessa tre kanter, kan det inte finnas någon Hamilton-cykel.
Den resulterande grafen är 3-kopplad och plan , så enligt Steinitz sats är det grafen för en polyeder. Den har 25 ansikten.
Det kan realiseras geometriskt från en tetraeder (vars ytor motsvarar de fyra stora niosidiga ytorna på ritningen, varav tre är mellan par av fragment och varav den fjärde utgör exteriören) genom att multiplicera trunkering av tre av dess hörn .
Algebraiska egenskaper
Automorfismgruppen i Tutte-grafen är Z /3 Z , den cykliska gruppen av ordning 3.
Det karakteristiska polynomet för Tutte-grafen är:
Relaterade grafer
Även om Tutte-grafen är den första 3-regelbundna icke-Hamiltonska polyedriska grafen som har upptäckts, är det inte den minsta sådana grafen.
1965 hittade Lederberg grafen Barnette–Bosák–Lederberg på 38 hörn. 1968 konstruerade Grinberg ytterligare små motexempel till taitens gissningar – Grinberg-graferna på 42, 44 och 46 hörn. 1974 publicerade Faulkner och Younger ytterligare två grafer - Faulkner-Younger-graferna på 42 och 44 hörn.
Slutligen visade Holton och McKay att det finns exakt sex 38-vertex icke-Hamiltonska polyedrar som har icke-triviala trekantssnitt. De bildas genom att ersätta två av hörnen på ett femkantigt prisma med samma fragment som används i Tuttes exempel.


