Sextisk ekvation

Graf över en sextisk funktion, med 6 reella rötter (korsningar av x -axeln) och 5 kritiska punkter . Beroende på antalet och vertikala placeringar av minima och maxima kan sextiken ha 6, 4, 2 eller inga riktiga rötter. Antalet komplexa rötter är lika med 6 minus antalet reella rötter.

I algebra är ett sextiskt (eller hexiskt ) polynom ett polynom med grad sex. En sextisk ekvation är en polynomekvation av grad sex – det vill säga en ekvation vars vänstra sida är ett sextiskt polynom och vars högra sida är noll. Mer exakt har den formen:

$ax^{6}+bx^{5}+cx^{4}+dx^{ 3}+ex^{2}+fx+g=0,\,$

där a ≠ 0 och koefficienterna a , b , c , d , e , f , g kan vara heltal , rationella tal , reella tal , komplexa tal eller mer allmänt medlemmar av vilket fält som helst .

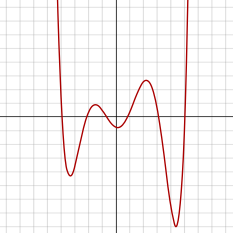
En sextisk funktion är en funktion som definieras av ett sextiskt polynom. Eftersom de har en jämn grad, verkar sextiska funktioner likna kvartsfunktioner när de är grafiska, förutom att de kan ha ett extra lokalt maximum och lokalt minimum vardera. Derivatan sextisk funktion är en kvintisk funktion .

Eftersom en sextisk funktion definieras av ett polynom med jämn grad, har den samma oändliga gräns när argumentet går till positiv eller negativ oändlighet . Om den ledande koefficienten a är positiv så ökar funktionen till positiv oändlighet på båda sidor och därmed har funktionen ett globalt minimum. På samma sätt, om a är negativ, minskar den sextiska funktionen till negativ oändlighet och har ett globalt maximum.

Lösbar sextik

Vissa sjättegradsekvationer, som ax ⁶ + dx ³ + g = 0 , kan lösas genom att faktorisera till radikaler, men andra sextiker kan inte. Évariste Galois utvecklade tekniker för att avgöra om en given ekvation kunde lösas av radikaler som gav upphov till området Galois teori .

Det följer av Galois teori att en sextisk ekvation är lösbar i termer av radikaler om och endast om dess Galois-grupp ingår antingen i gruppen av ordning 48 som stabiliserar en uppdelning av mängden rötter i tre delmängder av två rötter eller i grupp av ordningen 72 som stabiliserar en uppdelning av uppsättningen av rötter i två delmängder av tre rötter.

Det finns formler för att testa båda fallen, och, om ekvationen är lösbar, beräkna rötterna i termer av radikaler.

Den allmänna sextiska ekvationen kan lösas i termer av Kampé de Fériet-funktioner . En mer begränsad klass av sextiker kan lösas i termer av generaliserade hypergeometriska funktioner i en variabel genom att använda Felix Kleins metod för att lösa den kvintiska ekvationen .

Exempel

Watts kurva , som uppstod i samband med tidigt arbete med ångmaskinen , är en sextik i två variabler.

En metod för att lösa den kubiska ekvationen innebär att transformera variabler för att erhålla en sextisk ekvation som endast har termer av graderna 6, 3 och 0, som kan lösas som en andragradsekvation i variabelns kub.

Etymologi

Beskrivaren "sextisk" kommer från den latinska stammen för 6 eller 6 ("sex-t-"), och det grekiska suffixet som betyder "angående" ("-ic"). Den mycket mindre vanliga "hexic" använder grekiska för både sin stam ( hex- 6) och dess suffix ( -ik- ). I båda fallen hänvisar prefixet till graden av funktionen. Ofta kommer dessa typer av funktioner helt enkelt att kallas "6:e gradens funktioner".

Se även

• Cayley är sextisk
• Kubisk funktion
• Septisk ekvation