Linjär funktion (kalkyl)

Ej att förväxla med linjär funktionell eller linjär karta .

Graf för den linjära funktionen: $y(x)=-x+2$

I kalkyl och relaterade områden av matematik är en linjär funktion från de reella talen till de reella talen en funktion vars graf (i kartesiska koordinater ) är en icke-vertikal linje i planet. Den karakteristiska egenskapen för linjära funktioner är att när ingångsvariabeln ändras är förändringen i utsignalen proportionell mot förändringen i ingången.

Linjära funktioner är relaterade till linjära ekvationer .

Egenskaper

En linjär funktion är en polynomfunktion där variabeln x har graden högst ett:

$f(x)=ax+b$ .

En sådan funktion kallas linjär eftersom dess graf , mängden av alla punkter $(x,f(x))$ i det kartesiska planet , är en linje . Koefficienten a kallas lutningen för funktionen och linjen (se nedan).

Om lutningen är $a=0$ , är detta en konstant funktion $f(x)=b$ som definierar en horisontell linje, som vissa författare exkluderar från klassen linjära funktioner . Med denna definition skulle graden av ett linjärt polynom vara exakt ett, och dess graf skulle vara en linje som varken är vertikal eller horisontell. I den här artikeln krävs dock ${\displaystyle a\neq 0} , så konstanta funktioner kommer att betraktas som linjära.$

Om $b=0$ sägs den linjära funktionen vara homogen . En sådan funktion definierar en linje som går genom origo för koordinatsystemet, det vill säga punkten $(x,y)=(0,0)$ . I avancerade matematiktexter betecknar termen linjär funktion ofta specifikt homogena linjära funktioner, medan termen affin funktion används för det allmänna fallet, som inkluderar $b\neq 0$ .

Den naturliga domänen för en linjär funktion ${\displaystyle f(x)} ,$ mängden tillåtna ingångsvärden för x , är hela uppsättningen av reella tal , $x\in \mathbb {R} .$ Man kan också betrakta sådana funktioner med x i ett godtyckligt fält , med koefficienterna a, b i det fältet.

Grafen $y=f(x)=ax+b$ är en icke-vertikal linje som har exakt en skärningspunkt med y -axeln, dess y - skärningspunkt $(x,y)=(0,b).$$f(x).$ -skärningsvärdet y $\displaystyle y=f(0)=b}$ kallas också för det initiala värdet av x Om $a\neq 0,$ är grafen en icke-horisontell linje som har exakt en skärningspunkt med x -axeln, x -skärningspunkten $},0).}$ } x -skärningsvärdet $x=-{\tfrac {b}{ a}},$ lösningen av ekvationen $f(x)=0,$ kallas också roten eller nollan av $f(x).$

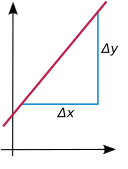
Backe

Lutningen på en linje är förhållandet ${\tfrac {\Delta y}{\Delta x}}$ mellan en förändring i x , betecknad $\Delta x$ , och motsvarande förändring i y , betecknad $\Delta y$

Lutningen på en icke-vertikal linje är ett tal som mäter hur brant linjen lutar (upp-över-körning) . Om linjen är grafen för den linjära funktionen ${\displaystyle f(x)=ax+b} ,$ ges denna lutning av konstanten a .

Lutningen mäter den konstanta förändringshastigheten för $f(x)$ per enhetsändring i x : närhelst ingången x ökas med en enhet ändras utmatningen med a enheter: $f(x{+}1)=f(x)+a$ , och mer allmänt $f (x{+}\Delta x)=f(x)+a\Delta x$ för valfritt tal $\Delta x$ . Om lutningen är positiv, ${\displaystyle a>0} , då$ ökar funktionen ${\displaystyle f(x)} ;$ om $a<0$ , då minskar $f(x)$

I kalkyl mäter derivatan av en allmän funktion dess förändringshastighet. En linjär funktion $f(x)=ax+b$ har en konstant förändringshastighet lika med dess lutning a , så dess derivata är konstantfunktionen $f\,'(x)=a$ .

Den grundläggande idén med differentialkalkyl är att varje jämn funktion $f(x)$ (inte nödvändigtvis linjär) kan approximeras nära en given punkt $x=c$ med en unik linjär fungera. Derivatan $f\,'(c)$ är lutningen för denna linjära funktion, och approximationen är: $f(x)\approx f\,'(c)(x{-}c)+f(c)$ f för $x\approx c$ . Grafen för den linjära approximationen är tangentlinjen för grafen $y=f(x)$ vid punkten $(c,f(c) )$ . Den derivativa lutningen $f\,'(c)$ varierar i allmänhet med punkten c . Linjära funktioner kan karakteriseras som de enda reella funktionerna vars derivata är konstant: om $f\,'(x)=a$ för alla x , då $f(x)=ax+b$ för $b=f(0)$ .

Slope-intercept, punkt-lutning och tvåpunktsformer

En given linjär funktion $f(x)$ kan skrivas i flera standardformler som visar dess olika egenskaper. Den enklaste är lutningsskärningsformen :

$f(x)=ax+b$ ,

från vilken man omedelbart kan se lutningen a och det initiala värdet $f(0)=b$ , vilket är y -skärningen av grafen $y=f (x)$ .

Givet en lutning a och ett känt värde ${\displaystyle f(x_{0})=y_{0}} ,$ skriver vi punkt-lutningsformen :

$f(x)=a(x{-}x_{0})+y_{0}$ .

I grafiska termer ger detta linjen $y=f(x)$ med lutningen a som går genom punkten $(x_{0},y_{0})$ .

Tvåpunktsformen börjar med två kända värden $displaystyle f(x_{0})=y_{0}}$$f(x_{1} )=y_{1}$ och 1 . Man beräknar lutningen $a={\tfrac {y_{1}-y_{0}}{x_{1}-x_{0}}}$ och infogar detta i punkt-lutningsformen:

$f(x)={\tfrac {y_{1}-y_{0}}{x_{1}-x_{ 0}}}(x{-}x_{0}\!)+y_{0}$ .

Dess graf $y=f(x)$ är den unika linjen som går genom punkterna $(x_{0},y_{ 0}\!),(x_{1},y_{1}\!)$ . Ekvationen $y=f(x)$ kan också skrivas för att betona den konstanta lutningen:

${\frac {y-y_{0}}{x-x_{0}}}={\frac {y_{1}-y_{ 0}}{x_{1}-x_{0}}}$ .

Samband med linjära ekvationer

Linjära funktioner uppstår vanligtvis från praktiska problem som involverar variabler $x,y$ med ett linjärt samband, det vill säga att följa en linjär ekvation $Ax+By=C$ . Om $B\neq 0$ , kan man lösa denna ekvation för y ,

$y=-{\tfrac {A}{B}}x+{\tfrac {C}{B}}=ax+b,$

där vi betecknar $a=-{\tfrac {A}{B}}$ och $b={\tfrac {C}{B}}$ . Det vill säga, man kan betrakta y som en beroende variabel (output) erhållen från den oberoende variabeln (input) x via en linjär funktion: $y=f(x)=ax +b$ . I xy -koordinatplanet bildar de möjliga värdena för $(x,y)$ en linje, grafen för funktionen $f(x)$ . Om $B=0$ i den ursprungliga ekvationen är den resulterande linjen $x={\tfrac {C}{A}}$ vertikal och kan inte skrivas som $y=f(x)$ .

Funktionerna i grafen $y=f(x)=ax+b$ kan tolkas i termer av variablerna x och y . Y -avsnittet är det initiala värdet $\displaystyle y=f(0)=b}$ { vid $x=0$ . Lutningen a mäter ändringshastigheten för utgången y per enhetsändring i ingången x . I grafen flyttar du en enhet åt höger (ökar x med 1) flyttar y -värdet upp med a : det vill säga $f(x{+} 1)=f(x)+a$ . Negativ lutning a indikerar en minskning av y för varje ökning av x .

Till exempel har den linjära funktionen $y=-2x+4$ lutning $a=-2$ , y -skärningspunkt $(0,b)=(0,4)$ och x -skärningspunkt $(2,0)$ .

Exempel

Anta att salami och korv kostar €6 och €3 per kilo, och vi vill köpa till ett värde av €12. Hur mycket av varje kan vi köpa? Om x kilo salami och y kilo korv kostar totalt 12 euro så är 6x x + 3x y euro 12 euro. Att lösa för y ger punktlutningsformen ${\displaystyle y=-2x+4} ,$ som ovan. Det vill säga, om vi först väljer mängden salami x , kan mängden korv beräknas som en funktion $y=f(x)=-2x+4$ . Eftersom salami kostar dubbelt så mycket som korv, minskar korven med 2 kilo om man lägger till ett kilo salami: $f(x{+}1)=f(x) -2$ , och lutningen är −2. Y -skärningspunkten ${\displaystyle (x,y)=(0,4)} motsvarar att köpa$ endast 4 kg korv; medan x -skärningspunkten $(x,y)=(2,0)$ motsvarar att köpa endast 2 kg salami.

Observera att grafen innehåller punkter med negativa värden på x eller y , som inte har någon betydelse i termer av de ursprungliga variablerna (såvida vi inte föreställer oss att sälja kött till slaktaren). Därför bör vi begränsa vår funktion $f(x)$ till domänen $0\leq x\leq 2$ .

Vi skulle också kunna välja y som den oberoende variabeln och beräkna x med den inversa linjära funktionen: $x=g(y)=-{\tfrac {1} {2}}y+2$ över domänen $0\leq y\leq 4$ .

Relation med andra klasser av funktioner

Om koefficienten för variabeln inte är noll ( a ≠ 0 ), så representeras en linjär funktion av ett grad 1 polynom (även kallat linjärt polynom ), annars är det en konstant funktion – också en polynomfunktion, men av noll grad .

En rät linje, när den dras i ett annat slags koordinatsystem, kan representera andra funktioner.

Till exempel kan den representera en exponentiell funktion när dess värden uttrycks i den logaritmiska skalan . Det betyder att när log ( g ( x )) är en linjär funktion av x är funktionen g exponentiell. Med linjära funktioner, ökar inmatningen med en enhet att utmatningen ökar med ett fast belopp, vilket är lutningen på grafen för funktionen. Med exponentialfunktioner, ökar inmatningen med en enhet att utsignalen ökar med en fast multipel, vilket är känt som basen för exponentialfunktionen.

Om både argument och värden för en funktion är i den logaritmiska skalan (dvs. när log ( y ) är en linjär funktion av log ( x ) ), representerar den räta linjen en potenslag :

$\log _{r}y=a\log _{r}x+b\quad \Rightarrow \quad y=r ^{b}\cdot x^{a}$

Arkimedeisk spiral definierad av den polära ekvationen r = 1 ⁄ 2 θ + 2

Å andra sidan, grafen för en linjär funktion i termer av polära koordinater :

$r=f(\theta )=a\theta +b$

är en arkimedisk spiral om $a\neq 0$ och en cirkel annars.

Se även

• Affin karta , en generalisering
• Aritmetisk progression , en linjär funktion av heltalsargument

Anteckningar

•   James Stewart (2012), Calculus: Early Transcendentals , upplaga 7E, Brooks/Cole. ISBN 978-0-538-49790-9
•   Swokowski, Earl W. (1983), Calculus with analytic geometri (Alternativ ed.), Boston: Prindle, Weber & Schmidt, ISBN 0871503417

externa länkar

• https://web.archive.org/web/20130524101825/http://www.math.okstate.edu/~noell/ebsm/linear.html
• http://www.corestandards.org/assets/CCSSI_Math%20Standards.pdf