Quantum dot cellulär automat

Quantum dot cellular automata (QDCA, ibland bara kallad quantum cellular automata , eller QCA) är en föreslagen förbättring av konventionell datordesign ( CMOS ), som har utformats i analogi med konventionella modeller av cellulära automater introducerade av John von Neumann .

Bakgrund

Varje enhet som är utformad för att representera data och utföra beräkningar, oavsett fysikprinciperna den utnyttjar och material som används för att bygga den, måste ha två grundläggande egenskaper: särskiljbarhet och villkorlig förändring av tillståndet, den senare innebär det förra. Detta innebär att en sådan anordning måste ha barriärer som gör det möjligt att skilja mellan stater, och att den måste ha förmågan att kontrollera dessa barriärer för att utföra villkorad tillståndsändring. Till exempel, i ett digitalt elektroniskt system transistorer rollen som sådana kontrollerbara energibarriärer, vilket gör det extremt praktiskt att utföra beräkningar med dem.

Cellulära automater

En cellulär automat (CA) är ett diskret dynamiskt system som består av ett enhetligt (ändligt eller oändligt) rutnät av celler. Varje cell kan endast vara i ett av ett ändligt antal tillstånd vid en diskret tidpunkt. När tiden går framåt bestäms tillståndet för varje cell i rutnätet av en transformationsregel som tar hänsyn till dess tidigare tillstånd och tillstånden för de omedelbart intilliggande cellerna (cellens "grannskap"). Det mest välkända exemplet på en cellulär automat är John Horton Conways " Game of Life ", som han beskrev 1970.

Kvantprickceller

Ursprung

Cellulära automater är vanligtvis implementerade som mjukvaruprogram. Men 1993, Lent et al. föreslog en fysisk implementering av en automat som använder kvantprickceller . Automaten blev snabbt populär och den tillverkades först 1997. Fastan kombinerade den diskreta karaktären hos både cellulära automater och kvantmekanik , för att skapa enheter i nanoskala som kan utföra beräkningar vid mycket höga växlingshastigheter (order Terahertz) och konsumera extremt litet mängder elektrisk kraft.

Moderna celler

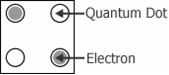
Idag, standard solid state QCA-celldesign anser att avståndet mellan kvantprickar är cirka 20 nm och ett avstånd mellan cellerna på cirka 60 nm. Precis som alla CA är Quantum (-dot) Cellular Automata baserade på de enkla interaktionsreglerna mellan celler placerade på ett rutnät . En QCA-cell är konstruerad av fyra kvantpunkter arrangerade i ett kvadratiskt mönster. Dessa kvantprickar är platser som elektroner kan uppta genom att tunnla till dem.

Celldesign

Figur 2 - Ett förenklat diagram över en QCA-cell med fyra punkter.

Figur 3 - De två möjliga tillstånden för en QCA-cell med fyra punkter.

Figur 2 visar ett förenklat diagram av en kvantpunktcell. Om cellen laddas med två elektroner, var och en fri att tunnla till vilken plats som helst i cellen, kommer dessa elektroner att försöka ockupera den längsta möjliga platsen i förhållande till varandra på grund av ömsesidig elektrostatisk repulsion . Därför finns det två särskiljbara celltillstånd. Figur 3 visar de två möjliga minimienergitillstånden för en kvantpunktcell. Tillståndet för en cell kallas dess polarisation , betecknad som P. Även om det är godtyckligt valt, har användning av cellpolarisation P = -1 för att representera logisk "0" och P = +1 för att representera logisk "1" blivit standardpraxis.

QCA tråd

Figur 4 - En tråd av kvantprickceller. Observera att de relativa avstånden mellan celler och punkter i en cell inte är skalenliga (celler är mycket längre ifrån varandra än punkter i en cell).

Rutnätsarrangemang av kvantprickceller beter sig på ett sätt som möjliggör beräkning. Det enklaste praktiska cellarrangemanget ges genom att placera kvantprickceller i serie , vid sidan av varandra. Figur 4 visar ett sådant arrangemang av fyra kvantprickceller. Begränsningsrutorna i figuren representerar inte fysisk implementering, utan visas som medel för att identifiera individuella celler.

Om polariseringen av någon av cellerna i arrangemanget som visas i figur 4 skulle ändras (med en "drivcell"), skulle resten av cellerna omedelbart synkroniseras till den nya polarisationen på grund av Coulombic interaktioner mellan dem . På detta sätt kan en "tråd" av kvantprickceller göras som sänder polarisationstillstånd. Konfigurationer av sådana ledningar kan bilda en komplett uppsättning logiska grindar för beräkning.

Det finns två typer av trådar möjliga i QCA: En enkel binär tråd som visas i figur 4 och en växelriktarkedja, som består av att placera 45-graders inverterade QCA-celler sida vid sida.

Logiska grindar

Majoritetsport

Majority gate och inverter (NOT) gate anses vara de två mest grundläggande byggstenarna i QCA. Figur 5 visar en majoritetsgrind med tre ingångar och en utgång. I denna struktur är den elektriska fälteffekten för varje ingång på utgången identisk och additiv, med resultatet att vilket ingångstillstånd som helst ("binärt 0" eller "binärt 1") som är i majoriteten blir utgångscellens tillstånd - därför portens namn. Till exempel, om ingångar A och B existerar i ett "binärt 0"-tillstånd och ingång C existerar i ett "binärt 1"-tillstånd, kommer utgången att existera i ett "binärt 0"-tillstånd eftersom den kombinerade elektriska fälteffekten av ingångarna A och B tillsammans är större än den för enbart ingång C.

Figur 5 - QCA Majority Gate

Andra portar

Andra typer av grindar, nämligen AND-grindar och ELLER-grindar , kan konstrueras med användning av en majoritetsgrind med fast polarisation på en av dess ingångar. En NOT-grind , å andra sidan, skiljer sig fundamentalt från majoritetsgrinden, som visas i figur 6. Nyckeln till denna design är att ingången delas och båda resulterande ingångarna träffar utgången snett. I motsats till en ortogonal placering tvingar den elektriska fälteffekten av denna ingångsstruktur fram en omkastning av polariseringen i utgången.

Figur 6 - Standardimplementering av en NOT-grind. Observera att märkningen av ingångs- och utdatavärden följer en konvention som är precis motsatt den i resten av den här artikeln.

Statsövergång

Figur 7 - QCA-klockan, dess stadier och dess effekter på en cells energibarriärer.

Det finns ett samband mellan kvantprickceller och cellulära automater. Celler kan bara vara i ett av två tillstånd och den villkorliga förändringen av tillståndet i en cell dikteras av tillståndet för dess närliggande grannar. En metod för att styra dataflöde är emellertid nödvändig för att definiera riktningen i vilken tillståndsövergång sker i QCA-celler. Klockorna i ett QCA-system har två syften: att driva automaten och styra dataflödets riktning . QCA-klockor är områden av ledande material under automatens gitter , som modulerar elektrontunnelbarriärerna i QCA-cellerna ovanför det.

Fyra etapper

En QCA-klocka inducerar fyra steg i tunnelbarriärerna för cellerna ovanför den. I det första skedet börjar tunnelbarriärerna stiga. Det andra steget uppnås när tunnelbarriärerna är tillräckligt höga för att förhindra elektroner från att tunnla. Det tredje steget inträffar när den höga barriären börjar sänkas. Och slutligen, i det fjärde steget, tillåter tunnelbarriärerna elektroner att fritt tunnla igen. Med enkla ord, när klocksignalen är hög, är elektroner fria att tunnla. När klocksignalen är låg låses cellen .

Figur 7 visar en klocksignal med dess fyra steg och effekterna på en cell vid varje klocksteg. En typisk QCA-design kräver fyra klockor, som var och en är cykliskt 90 grader ur fas med den tidigare klockan. Om en horisontell tråd bestod av säg 8 celler och varje på varandra följande par, med början från vänster, skulle anslutas till varje på varandra följande klocka, skulle data naturligt flöda från vänster till höger. Det första paret av celler kommer att förbli låst tills det andra paret av celler låses och så vidare. På detta sätt är dataflödesriktningen styrbar genom klockzoner

Trådkorsning

Figur 8 - Grundläggande trådkorsningsteknik. Observera att detta är schematiskt och att avstånden inte är skalenliga; celler är mycket längre ifrån varandra än prickar inuti celler.

Trådkorsning i QCA-celler kan göras genom att använda två olika kvantpunktsorienteringar (den ena i 45 grader till den andra) och låta en tråd som består av en typ passera vinkelrätt "genom" en tråd av den andra typen, som visas schematiskt i figur 8. Avstånden mellan prickarna i båda typerna av celler är exakt desamma, vilket ger samma coulombiska interaktioner mellan elektronerna i varje cell. Trådar som består av dessa två celltyper är emellertid olika: en typ sprider polarisering utan förändring; den andra vänder polarisering från en intilliggande cell till nästa. Interaktionen mellan de olika trådtyperna vid korsningspunkten ger ingen nettopolarisationsförändring i någon av trådarna, vilket gör att signalerna på båda trådarna kan bevaras.

Tillverkningsproblem

Även om denna teknik är ganska enkel, representerar den ett enormt tillverkningsproblem. En ny typ av cellmönster introducerar potentiellt så mycket som dubbelt så mycket tillverkningskostnad och infrastruktur; antalet möjliga kvantpunktsplatser på ett interstitiellt rutnät fördubblas och en övergripande ökning av geometrisk designkomplexitet är oundviklig. Ytterligare ett problem med denna teknik är att det extra utrymmet mellan celler med samma orientering minskar energibarriärerna mellan en cells grundtillstånd och en cells första exciterade tillstånd . Detta försämrar enhetens prestanda vad gäller maximal driftstemperatur, motstånd mot entropi och växlingshastighet.

Crossbar nätverk

En annan trådkorsningsteknik, som gör tillverkning av QCA-enheter mer praktisk, presenterades av Christopher Graunke, David Wheeler , Douglas Tougaw och Jeffrey D. Will i deras artikel "Implementation of a crossbar network using quantum-dot cellular automata" . Artikeln presenterar inte bara en ny metod för att implementera trådkorsningar, utan det ger också ett nytt perspektiv på QCA-klockning.

Deras trådkorsningsteknik introducerar konceptet att implementera QCA-enheter som kan utföra beräkningar som en funktion av synkronisering . Detta innebär möjligheten att modifiera enhetens funktion genom klockningssystemet utan att göra några fysiska ändringar på enheten. Sålunda åtgärdas det tidigare nämnda tillverkningsproblemet fullt ut genom att: a) använda endast en typ av kvantprickmönster och, b) genom förmågan att göra en universell QCA-byggsten med adekvat komplexitet, vilken funktion endast bestäms av dess tidsmekanism. (dvs. dess klockor).

Kvasi-adiabatisk omkoppling kräver emellertid att en cells tunnelbarriärer omkopplas relativt långsamt jämfört med den inneboende omkopplingshastigheten för en QCA. Detta förhindrar ringsignaler och metastabila tillstånd som observeras när celler byts abrupt. Därför begränsas omkopplingshastigheten för en QCA inte av den tid det tar för en cell att ändra polarisation, utan av den lämpliga kvasi-adiabatiska omkopplingstiden för de klockor som används.

Parallellt med seriell

När man designar en enhet som kan datorer är det ofta nödvändigt att konvertera parallella datalinjer till en seriell dataström . Denna omvandling gör att olika databitar kan reduceras till en tidsberoende serie av värden på en enda tråd. Figur 9 visar en sådan parallell-till-seriell konvertering QCA-enhet. Siffrorna på de skuggade områdena representerar olika klockningszoner vid på varandra följande 90-gradersfaser. Lägg märke till hur alla ingångar är på samma klockningszon. Om parallelldata skulle drivas vid ingångarna A, B, C och D, och sedan inte drivas mer under åtminstone de återstående 15 seriella överföringsfaserna , skulle utgången X presentera värdena för D, C, B och A -in den ordningen, vid fas tre, sju, elva och femton. Om en ny klockningsregion skulle läggas till vid utgången, skulle den kunna klockas för att låsa ett värde som motsvarar vilken som helst av ingångarna genom att korrekt välja en lämplig tillståndslåsningsperiod.

Den nya låsklockregionen skulle vara helt oberoende av de andra fyra klockningszonerna som illustreras i figur 9. Till exempel, om värdet av intresse för den nya låsningsregionen skulle vara det värde som D presenterar var 16:e fas, kommer klockmekanismen för ny region skulle behöva konfigureras för att låsa ett värde i den fjärde fasen och var 16:e fas från och med då, och därmed ignorera alla ingångar utom D.

Figur 9 - Parallell till seriell konvertering.

Ytterligare seriella linjer

Att lägga till en andra seriell linje till enheten och lägga till ytterligare ett låsområde skulle möjliggöra låsning av två ingångsvärden vid de två olika utgångarna. För att utföra beräkning läggs en grind som tar som ingångar båda seriella linjerna vid sina respektive utgångar. Grinden placeras över ett nytt låsområde konfigurerat att endast behandla data när båda låsområdena vid slutet av serielinjerna håller värdena av intresse vid samma ögonblick. Figur 10 visar ett sådant arrangemang. Om de är korrekt konfigurerade kommer låsområdena 5 och 6 var och en att hålla ingångsvärden av intresse för låsområdet 7. I detta ögonblick kommer låsområdet 7 att låta värdena låsta på områdena 5 och 6 genom OCH-grinden, så att utgången kan konfigureras till att vara OCH-resultatet av två valfria ingångar (dvs R och Q) genom att bara konfigurera låsområdena 5, 6 och 7.

Detta representerar flexibiliteten att implementera 16 funktioner, vilket lämnar den fysiska designen orörd. Ytterligare serielinjer och parallella ingångar skulle uppenbarligen öka antalet realiserbara funktioner. Emellertid är en betydande nackdel med sådana anordningar att, när antalet realiserbara funktioner ökar, krävs ett ökande antal klockningsregioner. Som en konsekvens kan en enhet som utnyttjar denna metod för funktionsimplementering fungera betydligt långsammare än sin traditionella motsvarighet.

Figur 10 – Multifunktions QCA-enhet.

Tillverkning

Generellt sett finns det fyra olika klasser av QCA-implementationer: metallö, halvledare, molekylär och magnetisk.

Metall-ö

Implementeringen av metallön var den första tillverkningstekniken som skapades för att demonstrera konceptet QCA. Det var ursprungligen inte tänkt att konkurrera med nuvarande teknik i bemärkelsen snabbhet och funktionalitet, eftersom dess strukturella egenskaper inte är lämpliga för skalbara konstruktioner. Metoden går ut på att bygga kvantprickar med hjälp av aluminiumöar. Tidigare experiment genomfördes med metallöar så stora som 1 mikrometer i dimension. På grund av de relativt stora öarna, var metallö-enheter tvungna att hållas vid extremt låga temperaturer för att kvanteffekter (elektronomkoppling) skulle kunna observeras.

Halvledare

Halvledar- (eller solid state ) QCA-implementeringar skulle potentiellt kunna användas för att implementera QCA-enheter med samma mycket avancerade halvledartillverkningsprocesser som används för att implementera CMOS-enheter. Cellpolarisering är kodad som laddningsposition, och kvantpunktsinteraktioner är beroende av elektrostatisk koppling. Men nuvarande halvledarprocesser har ännu inte nått en punkt där massproduktion av enheter med så små egenskaper (≈20 nanometer) är möjlig. Seriella litografiska metoder gör dock QCA solid state-implementering möjlig, men inte nödvändigtvis praktisk. Serielitografi är långsam, dyr och olämplig för massproduktion av solid-state QCA-enheter. Idag görs de flesta QCA-prototypexperiment med denna implementeringsteknik.

Molekyl

En föreslagen men ännu inte implementerad metod består av att bygga QCA-enheter av enstaka molekyler. De förväntade fördelarna med en sådan metod inkluderar: mycket symmetrisk QCA-cellstruktur, mycket höga omkopplingshastigheter, extremt hög enhetstäthet, drift vid rumstemperatur och till och med möjligheten att massproducera enheter med hjälp av självmontering. Ett antal tekniska utmaningar, inklusive val av molekyler, utformning av korrekta gränssnittsmekanismer och klockningsteknik återstår att lösa innan denna metod kan implementeras.

Magnetisk

Magnetisk QCA, vanligen kallad MQCA (eller QCA: M), är baserad på interaktionen mellan magnetiska nanopartiklar . Magnetiseringsvektorn för dessa nanopartiklar är analog med polarisationsvektorn i alla andra implementeringar. I MQCA hänvisar termen "Quantum" till den kvantmekaniska naturen hos magnetiska utbytesinteraktioner och inte till elektrontunneleffekterna. Enheter konstruerade på detta sätt kan fungera vid rumstemperatur.

Förbättring jämfört med CMOS

Komplementär metalloxid-halvledarteknologi (CMOS) har varit industristandarden för implementering av VLSI-enheter (Very Large Scale Integrated) under de senaste fyra decennierna, främst på grund av konsekvenserna av miniatyrisering av sådana enheter (dvs. ökande växlingshastigheter, ökande komplexitet och minskande Energiförbrukning). Quantum Cellular Automata (QCA) är bara en av de många alternativa tekniker som föreslås som en ersättningslösning för de grundläggande begränsningar som CMOS-tekniken kommer att införa under de kommande åren.

Även om QCA löser de flesta av begränsningarna med CMOS-teknik, ger den också sina egna. Forskning tyder på att den inneboende omkopplingstiden för en QCA-cell i bästa fall är i storleksordningen terahertz. Den faktiska hastigheten kan dock vara mycket lägre, i storleksordningen megahertz för halvledar-QCA och gigahertz för molekylär QCA, på grund av den korrekta kvasi-adiabatiska klockomkopplingsfrekvensen.

• Debashis De, Sitanshu Bhattacharaya och KP Ghatak, Quantum Dots and Quantum Cellular Automata: Senaste trender och tillämpningar, Nova, 2013
• Srivastava, S.; Asthana, A.; Bhanja, S.; Sarkar, S., "QCAPro - An error-power estimation tool for QCA circuit design," i Circuits and Systems (ISCAS), 2011 IEEE International Symposium on, vol., nr., s. 2377-2380, 15–18 maj 2011
• VV Zhirnov, RK Cavin, JA Hutchby och GI Bourianoff, "Gränser för skalning av binär logikomkopplare - En gedanken modell," Proc. IEEE, vol. 91, sid. 1934, november 2003.
• S. Bhanja och S. Sarkar, "Probabilistic Modeling of QCA Circuits using Bayesian Networks", IEEE Transactions on Nanotechnology, Vol. 5(6), sid. 657-670, 2006.
• S. Srivastava och S. Bhanja, "Hierarchical Probabilistic Macromodeling for QCA Circuits", IEEE Transactions on Computers, Vol. 56(2), sid. 174-190, februari 2007.
• Beth, T. Proceedings. "Quantum computing: an introduction" 2000 IEEE International Symposium on Circuits and Systems, 2000. Maj 2000 sid. 735-736 vol.1
• Victor V. Zhirnov, James A. Hutchby, George I. Bourianoff och Joe E. Brewer "Emerging Research Logic Devices" IEEE Circuits & Devices Magazine maj 2005 sid. 4
• Wolfram, Stephen " A New Kind of Science ", Wolfram Media May, 2002 sid. ix (Förord)
• CS Lent, P. Tougaw, W. Porod och G. Bernstein, "Quantum cellular automata" Nanotechnology, vol. 4, 1993 sid. 49-57.
• Victor V. Zhirnov, James A. Hutchby, George I. Bourianoff och Joe E. Brewer "Emerging Research Logic Devices" IEEE Circuits & Devices Magazine maj 2005 sid. 7
• Konrad Walus och GA Jullien "Quantum-Dot Cellular Automata Adders" Institutionen för el & dator Eng. University of Calgary Calgary, AB, Kanada sid. 4 - 6
• S. Henderson, E. Johnson, J. Janulis och D. Tougaw, "Inkorporering av standardmetoder för CMOS-designprocesser i QCA-logikdesignprocessen" IEEE Trans. Nanotechnology, vol. 3, nr. 1, mars 2004. sid. 2 - 9
• Christopher Graunke, David Wheeler, Douglas Tougaw, Jeffreay D. Will. "Implementering av ett gränsöverskridande nätverk med hjälp av kvantprickiga cellulära automater" IEEE Transactions on Nanotechnology, vol. 4, nr. 4 juli 2005 sid. 1 - 6
• G. T´oth och CS Lent, "Quasiadiabatic switching for metal-island quantum-dot cellular automata", Journal of Applied Physics, vol. 85, nr. 5, 1999 sid. 2977 - 2984
• G. T´oth, CS Lent, "Quantum computing with quantum-dot cellular automata", Physics Rev. A, vol. 63, 2000 sid. 1 - 9
• CS Lent, B. Isaksen, M. Lieberman, "Molecular Quantum-Dot Cellular Automata", J. Am. Chem. Soc., vol. 125, 2003 sid. 1056 - 1063
• K. Walus, GA Jullien, VS Dimitrov, "Computer Aritmetic Structures for Quantum Cellular Automata" Department of Electrical & Computer Eng. University of Calgary, Calgary, AB, Kanada sid. 1 - 4
• Rui Zhang, Pallav Gupta och Niraj K. Jha "Syntes av majoritets- och minoritetsnätverk och dess tillämpningar för QCA, TPL och SET-baserad nanoteknik" Proceedings of the 18th International Conference on VLSI Design som hölls tillsammans med 4th International Conference on Embedded Systems Design 2005 sid. 229-234
• De första publicerade rapporterna som introducerar konceptet Quantum Automaton:
• Baianu, I. 1971a. "Kategorier, funktioner och kvantautomatteori". Den 4:e Intl. Congress LMPS, augusti-sept.1971;
• Baianu, I.1971b. "Organismiska superkategorier och kvalitativa systemdynamik." Tjur. Matematik. Biophys., 33 (339-353): http://cogprints.ecs.soton.ac.uk/archive/00003674/01/ORganismic_supercategories_and_qualitative_dynamics_of_systems_final3.pdf .
• Niemier, M. 2004. Designing Digital Systems In Quantum Cellular Automata , Ph.D. avhandling, University of Notre Dame.
• Senaste uppdateringar :
• Quantum Reversible Automata : http://cogprints.org/3697/
• Quantum Nano-Automata. : http://doc.cern.ch/archive/electronic/other/ext/ext-2004-125/Quantumnanoautomata.doc
• Kategorier av Quantum Automata. : [1]

externa länkar

• [2] – QCA hemsida på Notre Dame