Olog

För de traditionella kvinnliga kommunala sovsalarna för Bontoc-folket på Filippinerna, se Dap-ay .

Teorin om ologer är ett försök att tillhandahålla en rigorös matematisk ram för kunskapsrepresentation, konstruktion av vetenskapliga modeller och datalagring med hjälp av kategoriteori, språkliga och grafiska verktyg. Ologer introducerades 2010 av David Spivak , en forskare vid Institutionen för matematik, MIT .

Etymologi

Termen "olog" är en förkortning för " ontologilogg ". "Ontologi" härstammar från onto- , från grekiskan ὤν , ὄντος "vara; det som är", presens particip av verbet εἰμί "vara", och -λογία , -logia : vetenskap , studie , teori .

Matematisk formalism

En olog ${\mathcal {C}}$ för en given domän är en kategori vars objekt är rutor märkta med fraser (mer specifikt singular obestämda substantivfraser) som är relevanta för domänen, och vars morfismer är riktade pilar mellan rutor, märkta med verbfraser som också är relevanta för domänen. Dessa substantiv- och verbfraser kombineras för att bilda meningar som uttrycker relationer mellan objekt i domänen.

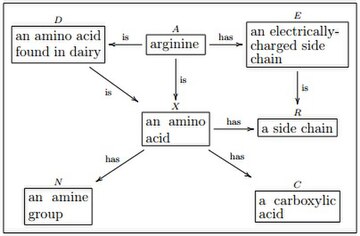
I varje olog finns objekten inom en målkategori . Om inget annat anges, anses målkategorin vara ${\displaystyle {\textbf {Set}}} ,$ kategorin för uppsättningar och funktioner . Rutorna i diagrammet ovan representerar objekt i ${\textbf {Set}}$ . Till exempel representerar rutan som innehåller frasen "en aminosyra" uppsättningen av alla aminosyror, och rutan som innehåller frasen "en sidokedja" representerar uppsättningen av alla sidokedjor. Pilen märkt "har" som pekar från "en aminosyra" till "en sidokedja" representerar funktionen som mappar varje aminosyra till dess unika sidokedja.

En annan målkategori som kan användas är Kleisli-kategorin ${\mathcal {C}}_{\mathbb {P} }$ för effektmängdsmonaden . Givet en ${\displaystyle A\in Ob({\textbf {Set}})} ,$ P $\displaystyle \mathbb {P} (A)}$ är då potensmängden för A Den naturliga transformationen $\eta$ mappar $a\in A$ till singeltonen $\{a\}$ och den naturliga transformationen $\mu$ mappar en uppsättning uppsättningar till dess förening. Kleisli- kategorin ${\mathcal {C}}_{\mathbb {P} }$ är kategorin med objekten som matchar de i $\mathbb {P}$ , och morfismer som etablerar binära relationer . Givet en morfism $f:A\to B$ , och givet $a\in A$ och $b\in B$ , definierar vi morfismen $R$ genom att säga att $(a,b)\in R$ närhelst $b\in f(a)$ . Verbfraserna som används med den här målkategorin skulle behöva vara vettiga med objekt som är delmängder: till exempel "är relaterad till" eller "är större än".

En annan möjlig målkategori är Kleisli-kategorin av sannolikhetsfördelningar, kallad Giry-monad. Detta ger en generalisering av Markovs beslutsprocesser .

Ologs och databaser

En olog ${\mathcal {C}}$ kan också ses som ett databasschema . Varje ruta (objekt av ${\mathcal {C}}$ ) i logen är en tabell $T$ och pilarna (morfismerna) som kommer från rutan är kolumner i ${\mathcal {C}}$ . Tilldelningen av en viss instans till ett objekt av ${\mathcal {C}}$ görs genom en funktion $I:{\mathcal {C}}\to {\textbf { Ställ in}}$ . I exemplet ovan kommer rutan "en aminosyra" att representeras som en tabell vars antal rader är lika med antalet typer av aminosyror och vars antal kolumner är tre, en kolumn för varje pil som kommer från den rutan.

Relationer mellan ologer

"Kommunikation" mellan olika ologer som i praktiken kan vara kommunikation mellan olika modeller eller världsbilder sker med hjälp av funktorer . Spivak myntar föreställningarna om en "meningsfull" och "starkt meningsfull" funktion. Låt ${\mathcal {C}}$ och ${\mathcal {D}}$ vara två loger, $I:{\mathcal {C}}\till { \textbf {Set}}$ , ${\displaystyle J:{\mathcal {D}}\till {\textbf {Set}}}-$ funktioner (se avsnittet om loggar och databaser) och $F:{\mathcal {C}}\to {\mathcal {D}}$ en funktor. $F$ kallas en schemamappning . Vi säger att en $F$ är meningsfull om det finns en naturlig transformation $m:I\to F^{*}J$ ( återgången av J med F).

Om man tar som exempel ${\mathcal {C}}$ och ${\mathcal {D}}$ som två olika vetenskapliga modeller, är funktorn $F$ meningsfull om "förutsägelser", som är objekt i ${\textbf {Set}}$ , gjorda av den första modellen ${\mathcal {C}}$ kan översättas till den andra modellen ${\mathcal {D }}$ .

Vi säger att $F$ är starkt meningsfullt om det ges ett objekt $X\i {\mathcal {C}}$ vi har $I(X)=J(F(X))$ . Denna likhet motsvarar att kräva att $m$ är en naturlig isomorfism.

Ibland kan det vara svårt att hitta en meningsfull funktion $F$ från ${\mathcal {C}}$ till ${\mathcal {D}}$ . I ett sådant fall kan vi försöka definiera en ny log ${\mathcal {B}}$ som representerar den gemensamma grunden för ${\mathcal {C}}$ och ${\mathcal {D}}$ och hitta meningsfulla funktioner $F_{\mathcal {C}}:{\mathcal {B}}\to {\mathcal {C}}$ och $F_{\mathcal {D}}:{\mathcal {B}}\to {\mathcal {D}}$ .

Om kommunikationen mellan ologer är begränsad till en tvåvägskommunikation som beskrivits ovan kan vi tänka på en samling ologer som noder i en graf och kanterna som funktorer som förbinder ologerna. Om en samtidig kommunikation mellan fler än två loger tillåts blir grafen ett symmetriskt förenklat komplex .

Regler för god praxis

Spivak ger några regler för god praxis för att skriva en olog vars morfismer har en funktionell karaktär (se det första exemplet i avsnittet Matematisk formalism). Texten i en ruta ska följa följande regler:

1. börja med ordet "a" eller "an". (Exempel: "en aminosyra").
2. hänvisa till en distinktion som görs och känns igen av ologens författare.
3. hänvisar till en distinktion för vilken det finns väldefinierad funktion vars intervall är ${\displaystyle {\textbf {Set}}} ,$ dvs en instans kan dokumenteras. (Exempel: det finns en uppsättning av alla aminosyror).
4. deklarera alla variabler i en sammansatt struktur. (Exempel: istället för att skriva i en ruta "en man och en kvinna" skriv "en man $m$ och en kvinna $w$ " eller "ett par $(m) ,w)$ där $m$ är en man och $w$ är en kvinna").

De tre första reglerna säkerställer att objekten (rutorna) som definieras av ologens författare är väldefinierade uppsättningar. Den fjärde regeln förbättrar märkningen av pilar i en olog.

Ansökningar

Detta koncept användes i en artikel publicerad i december 2011 av BioNanoScience av David Spivak och andra för att etablera en vetenskaplig analogi mellan spindelsilke och musikalisk komposition.

Se även

• Hypergraf
• Modelleringsspråk
• Ontologi språk
• Operateori
• Orgologi
• Universal algebra
• Universell logik

externa länkar

• Spivak, David I. "Kategorisk informatik" . math.mit.edu . Hämtad 2 maj 2017 .
•    Spivak, David I. (2014). Kategoriteori för vetenskaperna . Cambridge, MA: MIT Press . ISBN 9780262028134 . OCLC 876833252 .