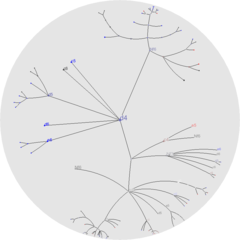
Hyperboliskt träd

Ett hyperboliskt träd (ofta förkortat som hyperträd ) är en metod för informationsvisualisering och grafritning inspirerad av hyperbolisk geometri .

Ett grundläggande hyperboliskt träd. Noder i fokus placeras i mitten och ges mer utrymme, medan ofokuserade noder komprimeras nära gränserna.

Fokusering på en annan nod tar den och dess barn till mitten av skivan, medan ointressanta delar av trädet komprimeras.

Att visa hierarkiska data som ett träd lider av visuell röran eftersom antalet noder per nivå kan växa exponentiellt. För ett enkelt binärt träd är det maximala antalet noder på en nivå n 2 ⁿ , medan antalet noder för träd med mer förgrening växer mycket snabbare. Att rita trädet som ett nodlänksdiagram kräver alltså exponentiella mängder utrymme för att visas.

Ett tillvägagångssätt är att använda ett hyperboliskt träd , först introducerat av Lamping et al. Hyperboliska träd använder hyperboliskt utrymme , som i sig har "mer utrymme" än euklidiskt utrymme. Om till exempel en linjär ökning av radien för en cirkel i det euklidiska rymden ökar dess omkrets linjärt, medan samma cirkel i det hyperboliska rymden skulle få sin omkrets att öka exponentiellt. Att utnyttja den här egenskapen gör det möjligt att lägga ut trädet i hyperboliskt utrymme på ett enkelt sätt: att placera en nod tillräckligt långt från sin förälder ger noden nästan samma mängd utrymme som sin förälder för att lägga ut sina egna barn.

Att visa ett hyperboliskt träd använder vanligtvis Poincaré-skivmodellen för hyperbolisk geometri, även om Klein-Beltrami- modellen också kan användas. Båda visar hela det hyperboliska planet inom en enhetsskiva, vilket gör hela trädet synligt på en gång. Enhetsskivan ger en fisheye-linsvy av planet, vilket ger mer betoning på noder som är i fokus och visar noder längre ur fokus närmare skivans gräns. Att korsa det hyperboliska trädet kräver Möbius-transformationer av rymden, vilket sätter nya noder i fokus och flyttar högre nivåer i hierarkin ur sikte.

Hyperbola träd patenterades i USA av Xerox 1996, men patentet har sedan dess gått ut.

Se även

• Hyperbolisk geometri
• Binär plattsättning
• Informationsvisualisering
• Radiellt träd – är också cirkulärt, men använder linjär geometri.
• Träd (datastruktur)
• Träd (grafteori)

externa länkar

• d3-hypertree – HTML5 Hyperbolic tree implementering, MIT licensierad
• Hyperbolic Tree of Life – Visualisering av livets träd med öppen källkod med Open Tree of Life-datauppsättning
• The Green Tree of Life – Livets träd – University of California i Berkeley och Jepson Herbaria
• Livets träd Liknar ovanstående, men med bilder
• RogueViz stöder hyperboliska träd.