Monokromatisk elektromagnetisk plan våg

I allmän relativitetsteori är den monokromatiska elektromagnetiska planvågen rymdtid analogen till de monokromatiska plana vågorna kända från Maxwells teori. Den exakta definitionen av lösningen är ganska komplicerad men mycket lärorik.

Varje exakt lösning av Einsteins fältekvation som modellerar ett elektromagnetiskt fält måste ta hänsyn till alla gravitationseffekter av energin och massan av det elektromagnetiska fältet . Förutom det elektromagnetiska fältet, om ingen materia och icke-gravitationella fält är närvarande, måste Einsteins fältekvation och Maxwells fältekvationer lösas samtidigt .

I Maxwells fältteori om elektromagnetism är en av de viktigaste typerna av ett elektromagnetiskt fält de som representerar elektromagnetisk mikrovågsstrålning . Av dessa är de viktigaste exemplen de elektromagnetiska planvågorna , där strålningen har plana vågfronter som rör sig i en specifik riktning med ljusets hastighet. Av dessa är den mest grundläggande de monokromatiska plana vågorna, i vilka endast en frekvenskomponent är närvarande. Detta är just det fenomen som denna lösning modellerar, men i termer av generell relativitet.

Definition av lösningen

Den metriska tensorn för den unika exakta lösningen som modellerar en linjärt polariserad elektromagnetisk planvåg med amplitud q och frekvens ω kan skrivas, i termer av Rosen-koordinater, i formen

$ds^{2}=-2\,du\,dv+C^{2}\left({\frac {q^{2}}{\omega ^{2}}},2{\frac {q^{2}}{\omega ^{2}}},\omega u\right)\,\left(dx^{2}+dy^{2}\right),\qquad -\infty <v ,x,y<\infty ,\quad -u_{0}<u<u_{0}.$

där $\xi ={\frac {u_{0}}{\omega }}$ är den första positiva roten av C ( a , 2 a , ξ ) = 0 där $a={\frac {q^{2}}{\omega ^{2}}}$ . I det här diagrammet är ∂ _u , ∂ _v nollkoordinatvektorer medan ∂ _x , ∂ _y är rymdliknande koordinatvektorer.

Här är Mathieu cosinus C ( a , b , ξ ) en jämn funktion som löser Mathieu-ekvationen och även tar värdet C ( a , b , 0) = 1 . Trots namnet är denna funktion inte periodisk, och den kan inte skrivas i termer av sinusformade eller till och med hypergeometriska funktioner. (Se Mathieu-funktionen för mer om Mathieu-kosinusfunktionen.)

I uttrycket för måtten, notera att ∂ _u , ∂ _v är nollvektorfält . Därför ∂ _u + ∂ _v ett tidsliknande vektorfält , medan ∂ _u − ∂ _v , ∂ _x , ∂ _y är rymdliknande vektorfält .

För att definiera det elektromagnetiska fältets vektorpotential kan man ta den elektromagnetiska fyrvektorpotentialen

${\ displaystyle {\vec {A}}={\frac {{\sqrt {2}}a\int C\left({\frac {u^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)\,\sin(\omega u)\,du}{C\left({\frac {q^{2 }}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}\;\partial _{x}}$

Detta är den fullständiga specifikationen av en matematisk modell formulerad i allmän relativitetsteori.

Lokala isometrier

Vår rymdtid är modellerad av ett Lorentziskt grenrör som har några anmärkningsvärda symmetrier. Vår rumtid tillåter nämligen en sexdimensionell Lie-grupp av självisometrier. Denna grupp genereras av en sexdimensionell Lie-algebra av dödande vektorfält . En bekväm bas består av ett nollvektorfält,

${\vec {\xi }}_{1}=\partial _{v}$

tre rymdliknande vektorfält,

${\vec {\xi }}_{2}=\partial _{x},\ ;{\vec {\xi}}_{3}=\partial _{y},\;{\vec {\xi}}_{4}=-y\,\partial _{x}+x\, \partial _{y}$

och ytterligare två vektorfält,

${\begin{aligned}{\vec {\xi }}_{5}&=x\,\partial _{v}+\int {\frac {du}{ C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right )}}\,\partial _{x}\\{\vec {\xi }}_{6}&=y\,\partial _{v}+\int {\frac {du}{C\left( {\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}\ ,\partial _{y}\end{aligned}}$

Här, ${\vec {\xi }}_{2},\,{\vec {\xi}}_{3},\,{\vec { \xi }}_{4}$ genererar den euklidiska gruppen , som verkar inom varje plan vågfront, vilket motiverar namnet planvåg för denna lösning. Även ${\vec {\xi }}_{5},\,{\vec {\xi }}_{6}$ visar att alla icke tvärgående riktningar är ekvivalenta. Detta motsvarar det faktum att två kolliderande plana vågor alltid kolliderar frontalt när de representeras i det lämpliga Lorentz-ramverket .

För framtida referens, notera att denna sexdimensionella grupp av självisometrier verkar transitivt så att vår rumtid är homogen . Det är dock inte isotropt , eftersom de tvärgående riktningarna skiljer sig från de icke-tvärgående.

En familj av tröghetsobservatörer

Ramfältet _

${\vec {e}}_{0}={\frac {1}{\sqrt {2}}}\left(\partial _{u} +\partial _{v}\right)$

${\vec {e}}_{1}={\frac {1}{\sqrt { 2}}}\left(-\partial _{u}+\partial _{v}\right)$

${\ displaystyle {\vec {e}}_{2}={\frac {1}{C\left({\frac {q^{2}}{\omega ^{2}}},\,{\frac { 2q^{2}}{\omega ^{2}}},\,\omega u\right)}}\partial _{x}}$

${\vec {e}}_{3}={\frac {1}{C\left({\frac {q^{2}}{\omega ^{2}} },\,{\frac {2q^{2}}{\omega ^{2}}},\,\omega u\right)}}\partial _{y}$

representerar den lokala Lorentz-ramen definierad av en familj av icke-snurrande tröghetsobservatörer . Det är,

$\nabla _{{\vec {e}}_{0}}{\vec {e}}_{0}=0$

vilket innebär att integralkurvorna för det tidslika enhetsvektorfältet e ₀ är tidsliknande geodesik , och även

$\nabla _{{\vec {e}}_{0}}{\vec {e}}_{1 }=\nabla _{{\vec {e}}_{0}}{\vec {e}}_{2}=\nabla _{{\vec {e}}_{0}}{\vec { e}}_{3}=0$

vilket betyder att de rymdliknande enhetsvektorfälten e ₁ , e ₂ , e ₃ är icke-snurrande. (De transporteras Fermi–Walker .) Här är ${\vec {e}}_{0}$ ett tidsliknande enhetsvektorfält, medan ${\displaystyle {\vec {e}}_{1},{\vec {e}}_{2},{\vec {e}}_{3}} är rymdliknande enhetsvektorfält$ .

Icke-snurrande tröghetsramar är så nära man kan komma i krökta rumstider till de vanliga Lorentz-ramverken kända från speciell relativitetsteori , där Lorentz-transformationer helt enkelt är förändringar från ett Lorentz-ramverk till ett annat.

Det elektromagnetiska fältet

När det gäller vår ram är det elektromagnetiska fältet som erhålls från potentialen som ges ovan

${\vec {E}}=q\,\sin(\omega u)\,{\vec {e}}_{2}$

${\vec {B}}=-q\,\sin(\omega u)\,{\vec {e}}_{3}$

Detta elektromagnetiska fält är en källfri lösning av Maxwell-fältekvationerna på den speciella krökta rymdtiden som definieras av den metriska tensorn ovan. Det är en nolllösning , och den representerar en tvärgående sinusformad elektromagnetisk planvåg med amplitud q och frekvens ω , som rör sig i e ₁ -riktningen. När man

• beräknar spännings-energitensorn T ^ab för det givna elektromagnetiska fältet,
• beräkna Einstein-tensorn Gab ^, för den givna metriska tensorn

man finner att Einsteins fältekvation Gab ^. = 8 πT ^ab är uppfylld Detta är vad som menas med att det finns en exakt elektrovakuumlösning .

När det gäller vår ram visar sig stress-energi-tensorn vara

$T^{{\hat {j}}{\hat {k}}}={\frac {q ^{2}\sin ^{2}(\omega u)}{4\pi }}{\begin{bmatrix}1&1&0&0\\1&1&0&0\\0&0&0&0\\0&0&0&0\end{bmatrix}}$

Detta är samma uttryck som man skulle hitta i klassisk elektromagnetism (där man försummar gravitationseffekterna av den elektromagnetiska fältenergin) för nollfältet som ges ovan; den enda skillnaden är att vår ram nu är en anholonomisk (ortonormal) bas på en krökt rumtid snarare än en koordinatbas i platt rumtid . (Se ramfält .)

Relativ rörelse hos observatörerna

Rosen-diagrammet sägs följa med vår familj av tröghetsobservatörer som inte snurrar, eftersom koordinaterna ve − u , x , y alla är konstanta längs varje världslinje, givet av en integralkurva för det tidslika enhetsvektorfältet ${\vec {X}}={\vec {e}}_{0}$ . Således, i Rosen-diagrammet, kan dessa observatörer tyckas vara orörliga. Men i själva verket är de i relativ rörelse i förhållande till varandra. För att se detta bör man beräkna deras expansionstensor för ramen som anges ovan. Detta visar sig vara

$\theta [{\vec {X}}]_{{\hat {i}}{\hat {j}}}={\frac {\omega }{\sqrt {2}}} \,{\frac {C^{\prime }({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2 }}},\omega u)}{C({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2} }},\omega u)}}\,\operatörsnamn {diag} (0,1,1)$

var

$C^{\prime }(a,q,\xi )={\frac {\partial C(a,q,\xi )}{\partial \xi }}.$

De icke-försvinnande komponenterna är identiska och är det

1. konkav ner på $-u_{0}<u<u_{0}$
2. försvinna vid u = 0 .

Fysiskt betyder detta att ett litet sfäriskt "moln" av våra tröghetsobservatörer tillfälligt svävar vid u = 0 och börjar sedan kollapsa, för att så småningom passera genom varandra vid u = u ₀ . Om man föreställer sig att de bildar ett tredimensionellt moln av likformigt fördelade testpartiklar, sker denna kollaps ortogonalt mot vågens utbredningsriktning. Molnet uppvisar ingen relativ rörelse i utbredningsriktningen, så detta är en rent tvärgående rörelse.

För ${\frac {q}{\omega }}\ll 1$ (kortvågsapproximationen) har man ca.

$g_{xx}\approx \cos(qu)^{2}$

$\tan(qu)}$${\displaystyle \theta [{\vec$$q=1/2,\omega = 5$ Till exempel, med , man har

där de exakta uttrycken plottas i rött och kortvågsapproximationerna i grönt.

Vorticitetstensorn för vår kongruens försvinner på samma sätt , så våra observatörers världslinjer är ortogonala över ytan . Hyperskivornas tredimensionella Riemann-tensor ges, angående vår ram, av

${{}^{3}R}_{1212}={{}^{3}R}_{1313}=q^ {2}\,\sin(\omega u)^{2}$

${{}^{3}R}_{2323}={\frac {-\omega ^{2}}{2}}\,{\frac {C ^{\prime }\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\ omega u\right)^{2}}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^ {2}}},\omega u\right)^{2}}}$

Krökningen delar sig prydligt i våg (sektionskrökningarna parallella med utbredningsriktningen) och bakgrund (den tvärgående sektionskrökningen).

Riemanns krökningstensor

Däremot är Bel-nedbrytningen av Riemann-kurvaturtensorn, taget med avseende på ${\displaystyle {\vec {X}}={\vec {e}}_{0}},$ enkelheten i sig. Den elektrogravitiska tensorn , som direkt representerar tidvattenaccelerationerna , är

$E[{\vec {X}}]_{{\hat {m}}{ \hat {n}}}=q^{2}\,\sin(\omega u)^{2}\,\operatörsnamn {diag} (0,1,1)$

Den magnetogravitiska tensorn , som direkt representerar spin-spinkraften på ett gyroskop som bärs av en av våra observatörer, är

$B[{\vec {X}}]_{{\hat {m}}{\hat { n}}}=q^{2}\,\sin(\omega u)^{2}{\begin{bmatrix}0&0&0\\0&0&-1\\0&1&0\end{bmatrix}}$

(Den topogravitiska tensorn , som representerar de rumsliga tvärsnittskrökningarna , överensstämmer med den elektrogravitiska tensorn.)

Om man tittar tillbaka på vår graf över den metriska tensorn kan man se att tidvattenstensorn producerar små sinusformade relativa accelerationer med perioden ω , som är rent tvärs mot vågens utbredningsriktning. Nettogravitationseffekten under många perioder är att producera en expansions- och återfallscykel av vår familj av tröghetsobservatörer som inte snurrar. Detta kan betraktas som effekten av vågens bakgrundskrökning .

Denna expansions- och återfallscykel påminner om de expanderande och återfallande FRW-kosmologiska modellerna , och den inträffar av en liknande anledning: närvaron av ickegravitationell massenergi. I FRW-modellerna beror denna massenergi på massan av stoftpartiklarna; här beror det på fältenergin i det elektromagnetiska vågfältet. Där börjar och slutar expansions-återkollapscykeln med en stark skalär krökningssingularitet ; här finns det bara en koordinerad singularitet (en omständighet som mycket förvirrade Einstein och Rosen 1937). Dessutom finns det en liten sinusformad modulering av expansionen och återkollapsen.

Optiska effekter

En allmän princip gällande plana vågor säger att man inte kan se vågtåget komma in på stationen, men man kan se det gå . Det vill säga, om man tittar genom mötande vågfronter på avlägsna objekt, kommer man inte att se någon optisk distorsion, men om man vänder sig och tittar genom avgående vågfronter på avlägsna objekt, kommer man att se optiska distorsioner . Specifikt den nollgeodesiska kongruensen som genereras av nollvektorfältet ${\vec {k}}={\vec {e}}_{0}+{\vec {e} }_{1}$ har försvinnande optiska skalärer , men noll geodetisk kongruens genererad av ${\vec {\ell }}={\vec {e}}_{0} -{\vec {e}}_{1}$ har försvinnande vridnings- och skjuvskalärer men icke-försvinnande expansionsskalärer

$\theta ={\sqrt {2}} \omega \,{\frac {C^{\prime }\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\ omega ^{2}}},\omega u\right)}{C\left({\frac {q^{2}}{\omega ^{2}}},{\frac {q^{2}} {2\omega ^{2}}},\omega u\right)}}$

Detta visar att när vi tittar genom avgående vågfronter på avlägsna objekt, kommer våra tröghetsobservatörer som inte snurrar att se deras uppenbara storlek förändras på samma sätt som expansionen av den tidslika geodetiska kongruensen själv.

Brinkmann-diagrammet

Ett sätt att snabbt se rimligheten i påståendet att u = u ₀ är en ren koordinatsingularitet är att komma ihåg att vår rumtid är homogen , så att alla händelser är likvärdiga. För att direkt bekräfta detta, och för att från ett annat perspektiv studera den relativa rörelsen hos våra tröghetsobservatörer som inte snurrar, kan man tillämpa koordinattransformationen

$u\to u$

$v\to v-{\frac {\dot {r}}{2r}}\left (x^{2}+y^{2}\right)$

$x\to x/r$

$y\to y/r$

var

$-{\frac {{\ddot {r}}(u)}{r(u)}}=q\sin( \omega u)^{2}$

Detta ger lösningen sin representation i termer av Brinkmann-koordinater :

$ds^{2 }=-q\,\sin(\omega u)^{2}\,du^{2}-2\,du\,dv+dx^{2}+dy^{2},\qquad -\infty <u,v,x,y<\infty$

Eftersom det kan visas att de nya koordinaterna är geodesiskt kompletta , definierar Brinkmann-koordinaterna ett globalt koordinatdiagram. I det här diagrammet kan man se att en oändlig sekvens av identiska expansion-återkollapscykler inträffar!

Frätande

I Brinkmann-diagrammet blir vårt ramfält ganska komplicerat:

${\vec {e}}_{0}={\frac {\partial _{u}+\partial _{v} }{\sqrt {2}}}+\left\{{\frac {x^{2}+y^{2}}{\sqrt {2}}}\left(-q^{2}\sin( \omega u)^{2}+{\frac {\omega ^{2}}{2}}\,{\frac {C^{\prime }\left({\frac {q^{2}}{ \omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)^{2}}{C\left({\frac { q^{2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)^{2}}}\ höger)\partial _{v}\right\}+\left\{{\frac {\omega }{2}}{\frac {C^{\prime }\left({\frac {q^{2} }{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}{C\left({\frac {q^ {2}}{\omega ^{2}}},{\frac {q^{2}}{2\omega ^{2}}},\omega u\right)}}\left(x\partial _ {x}+y\partial _{y}\right)\right\}$

och så vidare. Naturligtvis, om man beräknar expansionstensorn, elektrogravitisk tensor, och så vidare, skulle man få samma svar som tidigare men uttryckt i de nya koordinaterna.

Enkelheten hos den metriska tensorn jämfört med ramens komplexitet är slående. Poängen är att man lättare kan visualisera kaustiken som bildas av våra observatörers relativa rörelse i det nya diagrammet. Integralkurvorna för det tidslika enheten geodetiska vektorfältet ${\vec {X}}={\vec {e}}_{0}$ ger våra observatörers världslinjer. I Rosen-diagrammet visas dessa som vertikala koordinatlinjer, eftersom det diagrammet är på väg.

För att förstå hur denna situation ser ut i Brinkmann-diagrammet, lägg märke till att när ω är omfattande blir vårt tidslika geodetiska enhetsvektorfält ungefär

${\vec {X}}\approx {\frac {\partial _{u}+\partial _{v}}{\sqrt {2}}}-q\tan( qu)\left(x\partial _{x}+y\partial _{y}\right)+{\frac {x^{2}+y^{2}}{\sqrt {2}}}\, \left(-q^{2}\sin(\omega u)^{2}+q^{2}\tan(qu)^{2}\right)\partial _{v}$

Om man undertrycker den sista mandatperioden är resultatet

Ungefärlig rörelse av vår familj av observatörer, som representeras i Brinkmann-diagrammet

${\vec {X}}\approx \partial _{t}-q\tan \left({\ frac {qu}{\sqrt {2}}}\right)\left(x\partial _{x}+y\partial _{y}\right)$

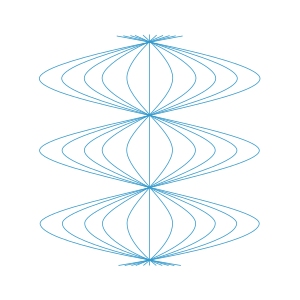
Man erhåller omedelbart en integralkurva som uppvisar sinusformade expansions- och återkonvergenscykler. Se figuren, där tiden löper vertikalt och man använder den radiella symmetrin för att undertrycka en rumslig dimension. Denna figur visar varför det finns en koordinatsingularitet i Rosen-diagrammet; observatörerna måste gå förbi varandra med jämna mellanrum, vilket är oförenligt med den kommande egenskapen, så sjökortet går sönder på dessa platser. Observera att denna siffra felaktigt antyder att en observatör är "attraktionens centrum", men i själva verket är de alla helt likvärdiga, på grund av den stora symmetrigruppen i denna rumtid. Observera också att den i stort sett sinusformade relativa rörelsen för våra observatörer är helt överensstämmande med beteendet hos expansionstensorn (beträffande ramfältet som motsvarar vår familj av observatörer) som noterades ovan.

Det är värt att notera att dessa lite knepiga punkter förvirrade inte mindre en figur än Albert Einstein i hans 1937 uppsats om gravitationsvågor (skriven långt innan det moderna matematiska maskineriet som används här blev allmänt uppskattat inom fysiken).

I Brinkmann-diagrammet är således världslinjerna för våra observatörer, i kortvågsfallet, periodiska kurvor som har formen av sinusformade med period ${\displaystyle 2\pi /q} ,$ modulerade av mycket mindre sinusformade störningar i nollriktningen ∂ _v och med en mycket kortare period, $2\pi /\omega$ . Observatörerna expanderar och kollapsar periodiskt på tvären till utbredningsdirektivet; denna rörelse moduleras av en kort period med små amplitudstörningar.

Sammanfattning

Genom att jämföra vår exakta lösning med den vanliga monokromatiska elektromagnetiska planvågen som behandlas i speciell relativitet (dvs. som en våg i platt rymdtid, som försummar gravitationseffekterna av energin i det elektromagnetiska fältet), ser man att den slående nya egenskapen i allmän relativitetsteori är de expansions- och kollapscykler som våra observatörer upplever, som man kan sätta ner till bakgrundskrökning , inte några mätningar gjorda över korta tider och avstånd (i storleksordningen av våglängden för den elektromagnetiska mikrovågsstrålningen).

Se även

• Argument för klibbiga pärlor , för en redogörelse för 1937 års tidning av Einstein och Rosen som anspelades på ovan.

•   Misner, Charles; Thorne, Kip S. & Wheeler, John Archibald (1973). Gravitation . San Francisco: WH Freeman . ISBN 0-7167-0344-0 . Se avsnitt 35.11