Likhet (nätverksvetenskap)
| Del av serie om | ||||
| nätverksvetenskapsteori | ||||
|---|---|---|---|---|
| Nätverkstyper | ||||
| Grafer | ||||
|
||||
| Modeller | ||||
|
||||
| ||||
Likhet i nätverksanalys uppstår när två noder (eller andra mer utarbetade strukturer) faller i samma ekvivalensklass.
Det finns tre grundläggande tillvägagångssätt för att konstruera mått på nätverkslikhet: strukturell ekvivalens, automorf ekvivalens och regelbunden ekvivalens. Det finns en hierarki av de tre ekvivalensbegreppen: vilken uppsättning strukturella ekvivalenser som helst är också automorfa och reguljära ekvivalenser. Varje uppsättning av automorfa ekvivalenser är också vanliga ekvivalenser. Alla regelbundna ekvivalenser är inte nödvändigtvis automorfa eller strukturella; och inte alla automorfa ekvivalenser är nödvändigtvis strukturella.
Visualisera likhet och avstånd
Clusterverktyg
Agglomerativ hierarkisk klustring av noder på basis av likheten mellan deras profiler av kopplingar till andra noder ger ett sammanfogningsträd eller Dendrogram som visualiserar graden av likhet mellan fall - och kan användas för att hitta ungefärliga ekvivalensklasser.
Multidimensionella skalningsverktyg
Vanligtvis är vårt mål i ekvivalensanalys att identifiera och visualisera "klasser" eller kluster av fall. När vi använder klusteranalys antar vi implicit att likheten eller avståndet mellan fall speglar en enda underliggande dimension. Det är dock möjligt att det finns flera "aspekter" eller "dimensioner" som ligger bakom de observerade likheterna mellan fall. Faktor- eller komponentanalys skulle kunna tillämpas på korrelationer eller kovarianser mellan fall. Alternativt kan flerdimensionell skalning användas (icke-metrisk för data som i sig är nominella eller ordinala; metriska för värderade).
MDS representerar mönstren av likhet eller olikhet i slipsprofilerna mellan aktörerna (när de tillämpas på närhet eller avstånd) som en "karta" i flerdimensionellt rum. Den här kartan låter oss se hur "nära" aktörer är, om de "kluster" i flerdimensionellt utrymme och hur mycket variation det finns längs varje dimension.
Strukturell motsvarighet
Två hörn i ett nätverk är strukturellt likvärdiga om de delar många av samma grannar.
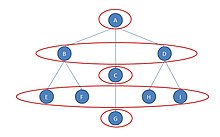
Det finns ingen skådespelare som har exakt samma band som skådespelare A, så skådespelare A är i en klass för sig. Detsamma gäller för aktörerna B, C, D och G. Var och en av dessa noder har en unik uppsättning kanter till andra noder. E och F faller dock i samma strukturella ekvivalensklass. Var och en har bara en kant; och den kopplingen är till B. Eftersom E och F har exakt samma mönster av kanter med alla hörn, är de strukturellt ekvivalenta. Detsamma gäller för H och I.
Strukturell ekvivalens är den starkaste formen av likhet. I många verkliga nätverk kan exakt ekvivalens vara sällsynt, och det kan vara användbart att förenkla kriterierna och mäta ungefärlig ekvivalens.
Ett närbesläktat begrepp är institutionell likvärdighet : två aktörer (t.ex. företag) är institutionellt likvärdiga om de verkar inom samma uppsättning institutionella områden. Medan strukturellt likvärdiga aktörer har identiska relationsmönster eller nätverkspositioner, fångar institutionell ekvivalens likheten mellan institutionella influenser som aktörer upplever från att vara inom samma områden, oavsett hur lika deras nätverkspositioner är. Till exempel kan två banker i Chicago ha mycket olika mönster av kopplingar (t.ex. kan den ena vara en central nod och den andra kan vara i en perifer position) så att de inte är strukturella motsvarigheter, utan eftersom de båda verkar på fältet inom finans och bank och inom samma geografiskt definierade område (Chicago), kommer de att utsättas för några av samma institutionella influenser.
Åtgärder för strukturell likvärdighet
Cosinus likhet
En enkel räkning av gemensamma grannar för två hörn är i sig inte ett särskilt bra mått. Man bör veta graden av hörn eller hur många gemensamma grannar andra hörnpar har. Cosinuslikhet tar hänsyn till dessa avseenden och tillåter även olika grader av hörn. Salton föreslog att vi skulle betrakta de i:te och j:te raden/kolumnerna i närliggande matris som två vektorer och använda cosinus för vinkeln mellan dem som ett likhetsmått . Cosinuslikheten för i och j är antalet gemensamma grannar dividerat med det geometriska medelvärdet av deras grader.
Dess värde ligger i intervallet från 0 till 1. Värdet 1 indikerar att de två hörnen har exakt samma grannar medan värdet noll betyder att de inte har några gemensamma grannar. Cosinuslikhet är tekniskt odefinierad om en eller båda noderna har nollgrad, men enligt konventionen säger vi att cosinuslikheten är 0 i dessa fall.
Pearson koefficient
Pearson produkt-moment korrelationskoefficient är en alternativ metod för att normalisera antalet vanliga grannar. Denna metod jämför antalet gemensamma grannar med det förväntade värdet som antalet skulle ta i ett nätverk där hörn är slumpmässigt anslutna. Denna kvantitet ligger strikt inom intervallet från -1 till 1.
Euklidiskt avstånd
Euklidiskt avstånd är lika med antalet grannar som skiljer sig mellan två hörn. Det är snarare ett olikhetsmått, eftersom det är större för hörn som skiljer sig mer åt. Det kan normaliseras genom att dividera med dess maximala värde. Maximum betyder att det inte finns några gemensamma grannar, i vilket fall avståndet är lika med summan av graderna på hörnen.
Automorf ekvivalens
Formellt "Två hörn är automorft ekvivalenta om alla hörn kan märkas om för att bilda en isomorf graf med beteckningarna för u och v utbytta. Två automorft ekvivalenta hörn delar exakt samma etikettoberoende egenskaper."
Mer intuitivt är aktörer automorft ekvivalenta om vi kan permutera grafen på ett sådant sätt att utbyte av de två aktörerna inte har någon effekt på avstånden mellan alla aktörer i grafen.
Antag att grafen beskriver ett företags organisationsstruktur. Aktör A är det centrala huvudkontoret, aktörerna B, C och D är chefer. Skådespelarna E, F och H, I är arbetare i mindre butiker; G är ensamarbetare i en annan butik.
Även om skådespelare B och skådespelare D inte är strukturellt likvärdiga (de har samma chef, men inte samma arbetare), verkar de vara "likvärdiga" i en annan mening. Både chef B och D har en chef (i det här fallet samma chef), och var och en har två arbetare. Om vi bytte dem, och även de fyra arbetarna, skulle alla avstånden mellan alla aktörer i nätverket vara exakt identiska.
Det finns faktiskt fem automorfa ekvivalensklasser: {A}, {B, D}, {C}, {E, F, H, I} och {G}. Observera att den mindre strikta definitionen av "ekvivalens" har minskat antalet klasser.
Regelbunden likvärdighet
Formellt, "Två skådespelare är regelbundet likvärdiga om de är lika släkt med likvärdiga andra." Med andra ord, regelbundet ekvivalenta hörn är hörn som, även om de inte nödvändigtvis delar grannar, har grannar som själva är lika.
Två mammor, till exempel, är likvärdiga, eftersom var och en har ett liknande mönster av förbindelser med en man, barn etc. De två mammorna har inte band till samma make eller samma barn, så de är inte strukturellt likvärdiga. Eftersom olika mödrar kan ha olika antal män och barn kommer de inte att vara automorfiskt likvärdiga. Men de är lika eftersom de har samma relationer med någon medlem eller medlemmar av en annan uppsättning skådespelare (som själva anses vara likvärdiga på grund av likheten mellan deras band med en medlem av uppsättningen "mamma").
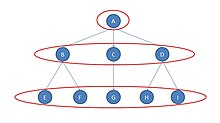
I grafen finns tre vanliga ekvivalensklasser. Den första är skådespelare A; den andra består av de tre skådespelarna B, C och D; den tredje består av de återstående fem skådespelarna E, F, G, H och I.
Den enklaste klassen att se är de fem skådespelarna längst ned i diagrammet (E, F, G, H och I). Dessa skådespelare är regelbundet likvärdiga med varandra eftersom:
- de har ingen koppling till någon skådespelare i första klassen (det vill säga med skådespelare A) och
- var och en har oavgjort med en skådespelare i andra klassen (antingen B eller C eller D).
Var och en av de fem skådespelarna har alltså ett identiskt mönster av band med skådespelare i de andra klasserna.
Skådespelarna B, C och D bildar en klass på liknande sätt. B och D har faktiskt band med två medlemmar i den tredje klassen, medan skådespelare C har en oavgjorthet till endast en medlem av den tredje klassen, men det spelar ingen roll, eftersom det finns en oavgjorthet till någon medlem i den tredje klassen.
Skådespelare A är i en klass för sig, definierad av:
- oavgjort till minst en medlem i klass två och
- ingen koppling till någon medlem i klass tre.
Se även
- ^ a b c d Newman, MEJ 2010. Nätverk: En introduktion. Oxford, Storbritannien: Oxford University Press.
- ^ a b c d e f g h Hanneman, Robert A. och Mark Riddle. 2005. Introduktion till sociala nätverksmetoder. Riverside, CA: University of California, Riverside (publicerad i digital form på http://faculty.ucr.edu/~hanneman/ )
- ^ a b Markis, Christopher; Tilcsik, András (2016-10-01). "Institutionell likvärdighet: Hur bransch- och gemenskapskollegor påverkar företagsfilantropi". Organisationsvetenskap . 27 (5): 1325–1341. doi : 10.1287/orsc.2016.1083 . hdl : 1813/44734 . ISSN 1047-7039 .
- ^ Salton G., Automatisk textbearbetning: Transformationen, analysen och hämtningen av information med dator, Addison-Wesley, Reading, MA (1989)
- ^ a b Borgatti, Steven, Martin Everett och Linton Freeman. 1992. UCINET IV Version 1.0 Användarhandbok. Columbia, SC: Analytic Technologies.