Hubbles lag

Hubbles lag , även känd som Hubble-Lemaître-lagen , är observationen inom fysisk kosmologi att galaxer rör sig bort från jorden med hastigheter som är proportionella mot deras avstånd. Med andra ord, ju längre de är, desto snabbare rör sig de bort från jorden. Galaxernas hastighet har bestämts av deras rödförskjutning , en förskjutning av ljuset de avger mot den röda änden av det synliga spektrumet .

₀ Hubbles lag anses vara den första observationsgrunden för universums expansion , och idag fungerar den som ett av de bevis som oftast citeras till stöd för Big Bang- modellen. Rörelsen av astronomiska föremål som enbart beror på denna expansion är känd som Hubble-flödet . Det beskrivs av ekvationen ₀ v = H D , med H proportionalitetskonstanten – Hubble-konstanten – mellan det "rätta avståndet" D till en galax, som kan förändras över tiden, till skillnad från det kommande avståndet , och dess separationshastighet v , dvs derivatan av korrekt avstånd med avseende på den kosmologiska tidskoordinaten . (Se Förflyttning och korrekta avstånd § Användning av rätt avstånd för en diskussion om finesserna i denna definition av "hastighet".)

₀₀₀₀ Hubble-konstanten anges oftast i ( km / s )/ Mpc , vilket ger hastigheten i km/s för en galax 1 megaparsec (3,09 × 10 ¹⁹ km) bort, och dess värde är cirka 70 (km/s)/ Mpc . Emellertid är SI-enheten för H helt enkelt s ⁻¹ , och SI-enheten för den reciproka av H är helt enkelt den andra. Den reciproka av H är känd som Hubble-tiden . Hubble-konstanten kan också tolkas som den relativa expansionshastigheten. I denna form H = 7 %/Gyr, vilket betyder att det vid nuvarande expansionstakt tar en miljard år för en obunden struktur att växa med 7 %.

₀ Även om det i stor utsträckning tillskrivs Edwin Hubble , härleddes föreställningen om att universum expanderar i en beräkningsbar hastighet först från allmänna relativitetsekvationer 1922 av Alexander Friedmann . Friedmann publicerade en uppsättning ekvationer, nu kända som Friedmann-ekvationerna , som visar att universum kan expandera, och presenterar expansionshastigheten om så vore fallet. Sedan kom Georges Lemaître , i en artikel från 1927, oberoende av att universum skulle expandera, observerade proportionaliteten mellan recessionshastighet för och avstånd till avlägsna kroppar och föreslog ett uppskattat värde för proportionalitetskonstanten; denna konstant, när Edwin Hubble bekräftade existensen av kosmisk expansion och bestämde ett mer exakt värde för den två år senare, kom att kallas under hans namn som Hubble-konstanten. Hubble härledde objektens recessionshastighet från deras rödförskjutningar , av vilka många tidigare uppmättes och relaterades till hastighet av Vesto Slipher 1917. Även om Hubble-konstanten H är konstant vid varje given tidpunkt, är Hubble-parametern H , varav Hubble-konstanten är det aktuella värdet, varierar med tiden, så termen konstant ses ibland som något av en felaktig benämning.

Upptäckt

Tre steg till Hubble-konstanten

Ett decennium innan Hubble gjorde sina observationer hade ett antal fysiker och matematiker etablerat en konsekvent teori om ett expanderande universum genom att använda Einsteins fältekvationer för allmän relativitet . Att tillämpa de mest allmänna principerna på universums natur gav en dynamisk lösning som stred mot den då rådande föreställningen om ett statiskt universum .

Sliphers iakttagelser

År 1912 mätte Vesto M. Slipher det första Dopplerskiftet av en " spiralnebulosa " (den föråldrade termen för spiralgalaxer) och upptäckte snart att nästan alla sådana nebulosor drog sig tillbaka från jorden. Han förstod inte de kosmologiska implikationerna av detta faktum, och på den tiden var det verkligen mycket kontroversiellt huruvida dessa nebulosor var "öuniversum" utanför vår Vintergatan eller inte.

FLRW-ekvationer

År 1922 härledde Alexander Friedmann sina Friedmann-ekvationer från Einsteins fältekvationer, vilket visade att universum kan expandera med en hastighet som kan beräknas av ekvationerna. Parametern som används av Friedmann är idag känd som skalfaktorn och kan betraktas som en skalinvariant form av proportionalitetskonstanten i Hubbles lag. Georges Lemaître hittade självständigt en liknande lösning i sitt papper från 1927 som diskuteras i följande avsnitt. Friedmann-ekvationerna härleds genom att infoga metriken för ett homogent och isotropiskt universum i Einsteins fältekvationer för en vätska med en given densitet och tryck . Denna idé om en expanderande rumtid skulle så småningom leda till Big Bang och Steady State teorier om kosmologi.

Lemaîtres ekvation

År 1927, två år innan Hubble publicerade sin egen artikel, var den belgiske prästen och astronomen Georges Lemaître den förste att publicera forskning som härledde vad som nu är känt som Hubbles lag. Enligt den kanadensiska astronomen Sidney van den Bergh , "upptäckten 1927 av universums expansion av Lemaître publicerades på franska i en tidskrift med låg inverkan. I 1931 års högeffektiva engelska översättning av denna artikel ändrades en kritisk ekvation genom att utelämna hänvisning till vad som nu är känt som Hubble-konstanten." Det är nu känt att ändringarna i den översatta tidningen utfördes av Lemaître själv.

Universums form

Före tillkomsten av modern kosmologi talades det mycket om universums storlek och form . 1920 Shapley-Curtis-debatten rum mellan Harlow Shapley och Heber D. Curtis om denna fråga. Shapley argumenterade för ett litet universum lika stor som Vintergatans galax, och Curtis hävdade att universum var mycket större. Problemet löstes under det kommande decenniet med Hubbles förbättrade observationer.

Cepheid variabla stjärnor utanför Vintergatan

Edwin Hubble gjorde det mesta av sitt professionella astronomiska observationsarbete vid Mount Wilson Observatory , hem till världens kraftfullaste teleskop vid den tiden. Hans observationer av Cepheid variabla stjärnor i "spiralnebulosor" gjorde det möjligt för honom att beräkna avstånden till dessa objekt. Överraskande nog upptäcktes dessa föremål vara på avstånd som placerade dem långt utanför Vintergatan. De fortsatte att kallas nebulosor , och det var bara gradvis som termen galaxer ersatte den.

Kombinera rödförskjutningar med avståndsmätningar

₀₀₀ Anpassning av rödförskjutningshastigheter till Hubbles lag. Det finns olika uppskattningar för Hubble-konstanten. HST Key H Group monterade supernovor av typ Ia för rödförskjutningar mellan 0,01 och 0,1 för att finna att H = 71 ± 2 (statistiskt) ± 6 (systematisk) km⋅s ⁻¹ ⋅Mpc ⁻¹ , medan Sandage et al. hitta H = 62,3 ± 1,3 (statistiskt) ± 5 (systematisk) km⋅s ⁻¹ ⋅Mpc ⁻¹ .

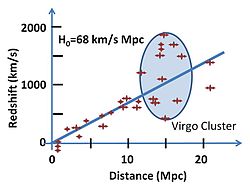
De parametrar som förekommer i Hubbles lag, hastigheter och avstånd, mäts inte direkt. I verkligheten bestämmer vi, säg, en supernovas ljusstyrka, som ger information om dess avstånd, och rödförskjutningen z = ∆ λ / λ av dess strålningsspektrum. Hubble-korrelerad ljusstyrka och parameter z .

Genom att kombinera sina mätningar av galaxavstånd med Vesto Slipher och Milton Humasons mätningar av de rödförskjutningar som är associerade med galaxerna, upptäckte Hubble en grov proportionalitet mellan rödförskjutning av ett objekt och dess avstånd. Även om det fanns avsevärd spridning (nu känt för att orsakas av speciella hastigheter - "Hubble-flödet" används för att hänvisa till området i rymden tillräckligt långt ut för att recessionshastigheten är större än lokala säregna hastigheter), kunde Hubble plotta en trendlinje från de 46 galaxer han studerade och få ett värde för Hubble-konstanten på 500 (km/s)/Mpc (mycket högre än det för närvarande accepterade värdet på grund av fel i hans avståndskalibreringar; se kosmisk avståndsstege för detaljer ) .

Vid tiden för upptäckten och utvecklingen av Hubbles lag var det acceptabelt att förklara rödförskjutningsfenomen som ett Dopplerskifte i samband med speciell relativitet, och använda Dopplerformeln för att associera rödförskjutning z med hastighet. Idag, i samband med allmän relativitet, beror hastigheten mellan avlägsna objekt på valet av koordinater som används, och därför kan rödförskjutningen lika beskrivas som en dopplerförskjutning eller en kosmologisk förskjutning (eller gravitation) på grund av det expanderande rymden, eller något kombination av de två.

Hubble diagram

Hubbles lag kan enkelt avbildas i ett "Hubble-diagram" där hastigheten (antagen ungefär proportionell mot rödförskjutningen) för ett föremål plottas med avseende på dess avstånd från betraktaren. En rak linje med positiv lutning på detta diagram är den visuella skildringen av Hubbles lag.

Kosmologisk konstant övergiven

Huvudartikel: Kosmologisk konstant

Efter att Hubbles upptäckt publicerats, övergav Albert Einstein sitt arbete med den kosmologiska konstanten , som han hade designat för att modifiera sina ekvationer av allmän relativitet för att tillåta dem att producera en statisk lösning, som han trodde var det korrekta tillståndet i universum. Einsteins ekvationer i sin enklaste formmodell genererade antingen ett expanderande eller sammandragande universum, så Einsteins kosmologiska konstant skapades på konstgjord väg för att motverka expansionen eller sammandragningen för att få ett perfekt statiskt och platt universum. Efter Hubbles upptäckt att universum i själva verket expanderade, kallade Einstein sitt felaktiga antagande att universum är statiskt för hans "största misstag". På egen hand skulle den allmänna relativitetsteorien kunna förutsäga universums expansion, som (genom observationer som ljusets böjning av stora massor eller precessionen av Merkurius bana ) kunde observeras experimentellt och jämföras med hans teoretiska beräkningar med hjälp av särskilda lösningar av de ekvationer han ursprungligen hade formulerat.

1931 gjorde Einstein en resa till Mount Wilson Observatory för att tacka Hubble för att ha tillhandahållit observationsgrunden för modern kosmologi.

Den kosmologiska konstanten har återuppmärksammats under de senaste decennierna som en hypotetisk förklaring till mörk energi .

Tolkning

En mängd möjliga recessionshastigheter kontra rödförskjutningsfunktioner inklusive den enkla linjära relationen v = cz ; en mängd möjliga former från teorier relaterade till allmän relativitet; och en kurva som inte tillåter hastigheter snabbare än ljus i enlighet med speciell relativitetsteori. Alla kurvor är linjära vid låga rödförskjutningar. Se Davis och Lineweaver.

Upptäckten av det linjära sambandet mellan rödförskjutning och avstånd, i kombination med ett förmodat linjärt samband mellan recessionshastighet och rödförskjutning, ger ett enkelt matematiskt uttryck för Hubbles lag enligt följande:

$v=H_{0}\,D$

var

• $v$ är recessionshastigheten, vanligtvis uttryckt i km/s.
• ₀0 H är Hubbles konstant och motsvarar värdet av $H$ (ofta kallad Hubble-parametern som är ett värde som är tidsberoende och som kan uttryckas i termer av skalfaktorn ) i Friedmann-ekvationerna tagna vid den tiden av observation som anges med teckningen . Detta värde är detsamma i hela universum under en given kommande tid .
• $D$ är det korrekta avståndet (som kan förändras över tiden, till skillnad från det kommande avståndet , som är konstant) från galaxen till observatören, mätt i megaparsecs (Mpc), i det 3-rum som definieras av en given kosmologisk tid . (Recessionshastigheten är bara v = dD/dt ).

Hubbles lag anses vara ett grundläggande förhållande mellan recessionshastighet och avstånd. Emellertid beror sambandet mellan recessionshastighet och rödförskjutning på den kosmologiska modellen som används och är inte etablerad förutom för små rödförskjutningar.

För avstånd D som är större än radien för Hubble-sfären r _HS , går objekt tillbaka med en hastighet som är snabbare än ljusets hastighet ( se Användning av rätt avstånd för en diskussion om betydelsen av detta):

$r_{\text{HS}}={\frac {c}{H_{0}}}\ .$

Eftersom Hubble-"konstanten" är en konstant endast i rymden, inte i tiden, kan Hubble-sfärens radie öka eller minska över olika tidsintervall. Den nedsänkta "0" indikerar värdet på Hubble-konstanten idag. Aktuella bevis tyder på att universums expansion accelererar ( se Accelererande universum ), vilket betyder att för en given galax ökar recessionshastigheten dD/dt över tiden när galaxen rör sig till allt större avstånd; men Hubble-parametern anses faktiskt minska med tiden, vilket betyder att om vi skulle titta på ett fast avstånd D och se en serie olika galaxer passera det avståndet, skulle senare galaxer passera det avståndet med en mindre hastighet än tidigare. .

Rödförskjutningshastighet och recessionshastighet

Rödförskjutning kan mätas genom att bestämma våglängden för en känd övergång, såsom väte-α-linjer för avlägsna kvasarer, och hitta fraktionsförskjutningen jämfört med en stationär referens. Rödförskjutning är således en storhet som är otvetydig för experimentell observation. Relationen mellan rödförskjutning och recessionshastighet är en annan sak. För en omfattande diskussion, se Harrison.

Rödförskjutningshastighet

Rödförskjutningen z beskrivs ofta som en rödförskjutningshastighet , vilket är den recessionella hastigheten som skulle producera samma rödförskjutning om den orsakades av en linjär dopplereffekt (vilket dock inte är fallet, eftersom förskjutningen delvis orsakas av en kosmologisk utvidgning av rymden , och eftersom de involverade hastigheterna är för stora för att använda en icke-relativistisk formel för Dopplerskifte). Denna rödförskjutningshastighet kan lätt överstiga ljusets hastighet. Med andra ord, för att bestämma rödförskjutningshastigheten v _rs , förhållandet:

$v_{\text{rs}}\equiv cz,$

är använd. Det vill säga, det finns ingen grundläggande skillnad mellan rödförskjutningshastighet och rödförskjutning: de är styvt proportionella och inte relaterade av något teoretiskt resonemang. Motivationen bakom "rödförskjutningshastighet"-terminologin är att rödförskjutningshastigheten överensstämmer med hastigheten från en låghastighetsförenkling av den så kallade Fizeau–Doppler-formeln .

$z={\frac {\lambda _{\text{o}}}{\lambda _{\text{e}}}}-1={\sqrt {\frac {1+{\frac {v }{c}}}{1-{\frac {v}{c}}}}}-1\approx {\frac {v}{c}}.$

Här är λ _o , λ _e de observerade respektive emitterade våglängderna. "Rödförskjutningshastigheten" v _rs är dock inte så enkelt relaterad till verklig hastighet vid högre hastigheter, och denna terminologi leder till förvirring om den tolkas som en verklig hastighet. Därefter diskuteras sambandet mellan rödförskjutnings- eller rödförskjutningshastighet och recessionshastighet. Denna diskussion är baserad på Sartori.

Recessionell hastighet

Antag att R(t) kallas universums skalfaktor och ökar när universum expanderar på ett sätt som beror på den valda kosmologiska modellen . Dess innebörd är att alla uppmätta korrekta avstånd D(t) mellan samgående punkter ökar proportionellt mot R . (De samtidigt rörliga punkterna rör sig inte i förhållande till varandra förutom som ett resultat av utvidgningen av rymden.) Med andra ord:

${\frac {D(t)}{D(t_{0})}}={\frac {R(t)} {R(t_{0})}},$

₀₀ där t är en viss referenstid. Om ljus sänds ut från en galax vid tidpunkten t _e och tas emot av oss vid t , rödförskjuts det på grund av rymdens expansion, och denna rödförskjutning z är helt enkelt:

$z={\frac {R(t_{0})}{R(t_{\text{e}})}}-1.$

Antag att en galax befinner sig på avstånd D , och detta avstånd ändras med tiden med en hastighet d _t D . Vi kallar denna lågkonjunktur för "recessionshastigheten" v _r :

$v_{\text{r}}=d_{t}D={\frac {d_{t}R}{R}}D.$

Vi definierar nu Hubble-konstanten som

$H\equiv {\frac {d_{t}R}{R}},$

och upptäck Hubble-lagen:

$v_{\text{r}}=HD.$

Ur detta perspektiv är Hubbles lag ett fundamentalt förhållande mellan (i) recessionshastigheten som tillförs av utvidgningen av rymden och (ii) avståndet till ett objekt; sambandet mellan rödförskjutning och avstånd är en krycka som används för att koppla ihop Hubbles lag med observationer. Denna lag kan relateras till rödförskjutning z ungefär genom att göra en Taylor-serieexpansion :

$z={\frac {R(t_{0})}{R(t_{e})}}-1\approx {\frac {R(t_{0})}{R(t_{0} )\left(1+(t_{e}-t_{0})H(t_{0})\right)}}-1\approx (t_{0}-t_{e})H(t_{0} ),$

Om avståndet inte är för stort blir alla andra komplikationer av modellen små korrigeringar, och tidsintervallet är helt enkelt avståndet dividerat med ljusets hastighet:

$z\approx (t_{0}-t_{\text{e}})H(t_{0})\approx {\frac {D}{c}}H(t_{0}),$

eller

$cz\approx DH(t_{0})=v_{r}.$

Enligt detta tillvägagångssätt är relationen cz = v _r en approximation som gäller vid låga rödförskjutningar, som ska ersättas av en relation vid stora rödförskjutningar som är modellberoende. Se figur för hastighet-rödförskjutning .

Observerbarhet av parametrar

Strängt taget är varken v eller D i formeln direkt observerbara, eftersom de är egenskaper nu hos en galax, medan våra observationer hänvisar till galaxen i det förflutna, vid den tidpunkt då ljuset vi för närvarande ser lämnade den.

För relativt närliggande galaxer (rödförskjutning z mycket mindre än enhet) kommer v och D inte att ha förändrats mycket, och v kan uppskattas med formeln $v=zc$ där c är ljusets hastighet. Detta ger det empiriska förhållandet som Hubble hittat.

För avlägsna galaxer kan v (eller D ) inte beräknas från z utan att specificera en detaljerad modell för hur H förändras med tiden. Rödförskjutningen är inte ens direkt relaterad till recessionshastigheten vid den tidpunkt då ljuset trädde ut, men den har en enkel tolkning: ( 1 + z ) är den faktor med vilken universum har expanderat medan fotonen färdades mot observatören.

Expansionshastighet vs relativ hastighet

När man använder Hubbles lag för att bestämma avstånd, kan endast hastigheten på grund av universums expansion användas. Eftersom gravitationellt interagerande galaxer rör sig i förhållande till varandra oberoende av universums expansion, måste dessa relativa hastigheter, som kallas säregna hastigheter, beaktas vid tillämpningen av Hubbles lag.

Finger of God -effekten är ett resultat av detta fenomen. I system som är gravitationsbundna , som galaxer eller vårt planetsystem, är utvidgningen av rymden en mycket svagare effekt än gravitationens attraktionskraft.

Tidsberoende av Hubble-parametern

Parametern $H$ kallas vanligtvis " Hubble-konstanten ", men det är en felaktig benämning eftersom den är konstant i rymden endast vid en fast tidpunkt; den varierar med tiden i nästan alla kosmologiska modeller, och alla observationer av långt avlägsna objekt är också observationer in i det avlägsna förflutna, när "konstanten" hade ett annat värde. " Hubble-parametern " är en mer korrekt term, där $H_{0}$ anger dagens värde.

En annan vanlig källa till förvirring är att det accelererande universum inte innebär att Hubble-parametern faktiskt ökar med tiden; eftersom ${\displaystyle H(t)\equiv {\dot {a}}(t)/a(t)} ,$ i de flesta accelererande modeller $a$ ökar relativt snabbare än ${\dot {a}}$ , så H minskar med tiden. (Recessionshastigheten för en vald galax ökar, men olika galaxer som passerar en sfär med fast radie korsar sfären långsammare vid senare tidpunkter.)

Om att definiera den dimensionslösa retardationsparametern

${\displaystyle q\equiv -{\frac {{\ddot {a}}\,a}{{\dot {a}}^{2}}}} , det följer$ att

${\frac {dH}{dt}}=-H^{2}(1+q)$

Av detta kan man se att Hubble-parametern minskar med tiden, såvida inte $q<-1$ ; det senare kan bara inträffa om universum innehåller fantomenergi , som betraktas som teoretiskt något osannolikt.

Men i standardmodellen för kall mörk materia Lambda (Lambda-CDM eller ΛCDM-modellen), kommer $q$ att tendera till −1 från ovan i en avlägsen framtid när den kosmologiska konstanten blir allt mer dominerande över materia; detta innebär att $H$ kommer att närma sig från ovan till ett konstant värde på ≈ 57 (km/s)/Mpc, och universums skalfaktor kommer då att växa exponentiellt med tiden.

Idealiserade Hubbles lag

Den matematiska härledningen av en idealiserad Hubbles lag för ett likformigt expanderande universum är en ganska elementär teorem om geometri i 3-dimensionellt kartesiskt /newtonskt koordinatrum, som betraktat som ett metriskt utrymme är helt homogent och isotropiskt (egenskaper varierar inte med plats eller riktning). Enkelt uttryckt är satsen denna:

Varje två punkter som rör sig bort från origo, var och en längs räta linjer och med hastighet proportionell mot avståndet från origo, kommer att röra sig bort från varandra med en hastighet som är proportionell mot deras avstånd från varandra.

I själva verket gäller detta icke-kartesiska utrymmen så länge de är lokalt homogena och isotropa, specifikt för de negativt och positivt krökta utrymmen som ofta betraktas som kosmologiska modeller (se universums form ) .

En observation som härrör från detta teorem är att att se objekt dra sig tillbaka från oss på jorden inte är en indikation på att jorden är nära ett centrum från vilket expansionen sker, utan snarare att varje observatör i ett expanderande universum kommer att se objekt som drar sig tillbaka från dem .

Universums ultimata öde och ålder

Universums ålder och slutliga öde kan bestämmas genom att mäta Hubble-konstanten idag och extrapolera med det observerade värdet av retardationsparametern, unikt kännetecknad av värden på densitetsparametrar (Ω _M för materia och Ω _Λ för mörk energi). Ett "stängt universum" med Ω _M > 1 och Ω _Λ = 0 tar slut i en Big Crunch och är betydligt yngre än Hubble-åldern. Ett "öppet universum" med Ω _M ≤ 1 och Ω _Λ = 0 expanderar för alltid och har en ålder som ligger närmare dess Hubble-ålder. För det accelererande universum med icke-noll Ω _Λ som vi bebor, är universums ålder av en slump väldigt nära Hubble-åldern.

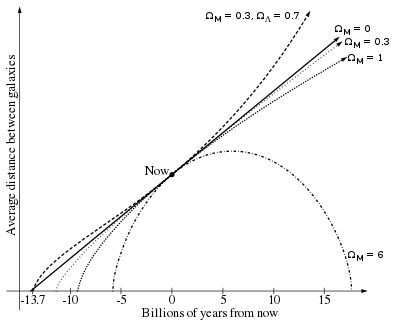
Värdet på Hubble-parametern ändras över tiden, antingen ökar eller minskar beroende på värdet på den så kallade retardationsparametern $q$ , som definieras av

$q=-\left(1+{\frac {\dot {H}}{H^{2}}}\right).$

I ett universum med en retardationsparameter lika med noll, följer att H = 1/ t , där t är tiden sedan Big Bang. Ett tidsberoende värde som inte är noll på $q$ kräver helt enkelt integrering av Friedmann-ekvationerna bakåt från den nuvarande tiden till den tid då den kommande horisontstorleken var noll.

Man trodde länge att q var positivt, vilket tyder på att expansionen saktar ner på grund av gravitationsattraktion. Detta skulle innebära en ålder av universum mindre än 1/ H (vilket är cirka 14 miljarder år). Till exempel skulle ett värde för q på 1/2 (en gång gynnat av de flesta teoretiker) ge universums ålder som 2/(3 H ). Upptäckten 1998 att q uppenbarligen är negativ betyder att universum faktiskt kan vara äldre än 1/ H . Uppskattningar av universums ålder är dock mycket nära 1/ H .

Olbers paradox

Huvudartikel: Olbers paradox

Utvidgningen av rymden som sammanfattas av Big Bang-tolkningen av Hubbles lag är relevant för den gamla gåtan som kallas Olbers paradox : Om universum var oändligt i storlek, statiskt och fyllt med en enhetlig fördelning av stjärnor , då skulle varje siktlinje i himlen skulle sluta på en stjärna, och himlen skulle vara lika ljus som ytan på en stjärna. Men natthimlen är i stort sett mörk.

Sedan 1600-talet har astronomer och andra tänkare föreslagit många möjliga sätt att lösa denna paradox, men den för närvarande accepterade lösningen beror delvis på Big Bang-teorin, och delvis på Hubble-expansionen: I ett universum som existerar för en begränsad mängd över tid har bara ljuset från ett ändligt antal stjärnor haft tillräckligt med tid för att nå oss, och paradoxen är löst. Dessutom, i ett expanderande universum, avlägsnar sig avlägsna objekt från oss, vilket gör att ljuset som utgår från dem förskjuts röd och minskar i ljusstyrka när vi ser det.

Dimensionslös Hubble-konstant

_{00 0} Istället för att arbeta med Hubbles konstant är en vanlig praxis att introducera den dimensionslösa Hubble-konstanten , vanligtvis betecknad med h och vanligen kallad "lilla h", och sedan skriva Hubbles konstant H som h × 100 km⋅ s ⁻¹ ⋅ Mpc ^{− 1} , all den relativa osäkerheten för det sanna värdet av H förpassas sedan till h . Den dimensionslösa Hubble-konstanten används ofta när man ger avstånd som beräknas från rödförskjutning z med formeln d ≈ c / H ₀ × z . Eftersom H inte är exakt känd uttrycks avståndet som:

$cz/H_{0}\approx (2998\times z){\text{ Mpc }}h^{-1}$

Med andra ord, man räknar ut 2998×z och man ger enheterna som ${\text{Mpc }}h^{-1}$ eller $h^{-1}{\text{ Mpc}}.$

Ibland kan ett annat referensvärde än 100 väljas, i vilket fall en subskript presenteras efter h för att undvika förvirring; t.ex. h ₇₀ betecknar $H_{0}=70\,h_{70}\,\mathrm {km{\cdot }s^{- 1}{\cdot }Mpc^{-1}}$ , vilket innebär $h_{70}=h/0.7$ .

₀₀ Detta ska inte förväxlas med det dimensionslösa värdet av Hubbles konstant, vanligtvis uttryckt i termer av Planck-enheter , erhållet genom att multiplicera H med 1,75 × 10 ⁻⁶³ (från definitioner av parsec och t _P ), till exempel för H = 70, en Planck enhetsversion på 1,2 × 10 ⁻⁶¹ erhålls.

Acceleration av expansionen

Huvudartikel: Accelererande expansion av universum

Ett värde för $q$ uppmätt från standardljusobservationer av supernovor av typ Ia , vilket fastställdes 1998 som negativt, förvånade många astronomer med innebörden att universums expansion för närvarande "accelererar" (även om Hubble-faktorn minskar fortfarande med tiden, som nämnts ovan i avsnittet Tolkning , se artiklarna om mörk energi och ΛCDM-modellen ).

Härledning av Hubble-parametern

Börja med Friedmanns ekvation :

$H^{2}\equiv \left({\frac {\dot {a}} {a}}\right)^{2}={\frac {8\pi G}{3}}\rho -{\frac {kc^{2}}{a^{2}}}+{\frac {\Lambda c^{2}}{3}},$

där $H$ är Hubble-parametern, $a$ är skalfaktorn , G är gravitationskonstanten , $k$ är universums normaliserade rumsliga krökning och lika med −1, 0 , eller 1, och $\Lambda$ är den kosmologiska konstanten.

Materiadominerat universum (med en kosmologisk konstant)

Om universum är materiadominerat kan universums masstäthet $\rho$ bara tas för att inkludera materia så

$\rho =\rho _{m}(a)={\frac {\rho _{m_{0}}}{a^{3}} },$

där $\rho _{m_{0}}$ är materiens densitet idag. Från Friedmann-ekvationen och termodynamiska principer vet vi för icke-relativistiska partiklar att deras massdensitet minskar proportionellt mot universums omvända volym, så ekvationen ovan måste vara sann. Vi kan också definiera (se densitetsparameter för $\Omega _{m}$ )

$\rho _{c}={\frac {3H_{0}^{2}}{8\pi G}};$

$\Omega _{m}\equiv {\frac {\rho _{m_{0}}}{\rho _{c}}}={\frac {8\pi G}{3H_{0}^ {2}}}\rho _{m_{0}};$

därför:

$\rho ={\frac {\rho _{c}\Omega _{m}}{a^{3}}}.$

Dessutom, per definition,

$\Omega _{k}\equiv {\frac {-kc^{2}}{(a_{0}H_{0})^{2}} }$

$\Omega _{\Lambda }\equiv {\frac {\Lambda c^{2}}{3H_{0}^{2}}},$

där det nedsänkta intet refererar till värdena idag, och $a_{0}=1$ . Att ersätta allt detta i Friedmann-ekvationen i början av detta avsnitt och ersätta $a$ med $a=1/(1+z)$ ger

$H^{2}(z)=H_{0}^{2}\left(\Omega _{m}(1+z)^{3}+\Omega _{k}(1+z) ^{2}+\Omega _{\Lambda }\right).$

Materia- och mörkenergidominerat universum

Om universum är både materiedominerat och mörkenergidominerat, så kommer ovanstående ekvation för Hubble-parametern också att vara en funktion av ekvationen för mörk energis tillstånd . Så nu:

$\rho =\rho _{m}(a)+\rho _{de}(a),$

där $\rho _{de}$ är den mörka energins masstäthet. Per definition är en tillståndsekvation i kosmologi ${\displaystyle P=w\rho c^{2}} ,$ och om denna ersätts med vätskeekvationen, som beskriver hur universums massdensitet utvecklas med tiden alltså

${\dot {\rho }}+3{\frac {\dot {a}}{a}}\left(\rho +{\frac {P}{c^{2}}}\right) =0;$

${\frac {d\rho }{\rho }}=-3{\frac {da}{a}}(1+w).$

Om w är konstant, då

$\ln {\rho }=-3(1+w)\ln {a};$

antyder:

$\rho =a^{-3(1+w)}.$

Därför, för mörk energi med en konstant ekvation för tillstånd w , $\rho _{de}(a)=\rho _{de0} a^{-3(1+w)}$ . Om detta ersätts i Friedman-ekvationen på liknande sätt som tidigare, men denna tidsuppsättning ${\displaystyle k=0} ,$ vilket antar ett rumsligt platt universum, då (se universums form )

$H^{2}(z)=H_{0}^{2}\left(\Omega _{m}(1+z)^{3}+\Omega _{de}(1+z) ^{3(1+w)}\höger).$

Om den mörka energin härrör från en kosmologisk konstant som den som introducerades av Einstein, kan det visas att $w=-1$ . Ekvationen reduceras sedan till den sista ekvationen i den materiadominerade universumsektionen, med $\Omega _{k}$ inställd på noll. I så fall ges den initiala mörka energitätheten ${\displaystyle \rho _{de0}} av$

$\rho _{de0}={\frac {\Lambda c^{2}}{8\pi G}}$ och $\Omega _{de}=\Omega _{\Lambda }.$

Om mörk energi inte har en konstant tillståndsekvation w, då

$}e^{-3 \int {\frac {da}{a}}\left(1+w(a)\right)},}$

och för att lösa detta måste $w(a)$ parametriseras, till exempel om $w(a)=w_{0} +w_{a}(1-a)$ , ger

$H^{2}(z)=H_{0}^{2}\left(\Omega _{m}a^{-3}+\Omega _{de}a^{-3\left( 1+w_{0}+w_{a}\right)}e^{-3w_{a}(1-a)}\right).$

Andra ingredienser har formulerats nyligen.

Enheter härledda från Hubble-konstanten

Hubble tid

Hubble-konstanten $H_{0}$ har enheter för invers tid; Hubbletiden t _H definieras helt enkelt som inversen av Hubblekonstanten, dvs

$t_{H}\equiv {\frac {1}{H_{0}}}={\frac {1}{67.8\mathrm {~(km/s)/Mpc} }}=4.55\ gånger 10 ^{17}\mathrm {~s} =14,4{\text{ miljarder år}}.$

Detta skiljer sig något från universums ålder som är cirka 13,8 miljarder år. Hubble-tiden är den ålder den skulle ha haft om expansionen hade varit linjär, och den skiljer sig från universums verkliga ålder eftersom expansionen inte är linjär; de är relaterade av en dimensionslös faktor som beror på universums massenergiinnehåll, vilket är cirka 0,96 i standardmodellen ΛCDM .

Vi verkar för närvarande närma oss en period där universums expansion är exponentiell på grund av vakuumenergins ökande dominans . I denna regim är Hubble-parametern konstant, och universum växer med en faktor e varje Hubble-tid:

$H\equiv {\frac {\dot {a}}{a}}={\textrm {konstant}}\quad \Longrightarrow \quad a\propto e^{Ht}=e^{\frac {t}{t_{H}}}$

På samma sätt betyder det allmänt accepterade värdet på 2,27 Es ⁻¹ att (med nuvarande takt) universum skulle växa med en faktor på $e^{2,27}$ på en exasekund .

Under långa tidsperioder kompliceras dynamiken av allmän relativitetsteori, mörk energi, inflation , etc., som förklarats ovan.

Hubble längd

Hubble-längden eller Hubble-avståndet är en enhet för avstånd i kosmologi, definierad som $cH_{0}^{-1}$ — ljusets hastighet multiplicerad med Hubble-tiden. Det motsvarar 4 420 miljoner parsek eller 14,4 miljarder ljusår. (Det numeriska värdet för Hubble-längden i ljusår är per definition lika med Hubble-tiden i år.) Hubble-avståndet skulle vara avståndet mellan jorden och de galaxer som för närvarande drar sig tillbaka från oss med en hastighet av ljus, som kan ses genom att ersätta $D=cH_{0}^{-1}$ i ekvationen för Hubbles lag, ₀ v = H D .

Hubble volym

Huvudartikel: Hubble volym

Hubble-volymen definieras ibland som en volym av universum med en kommande storlek på $cH_{0}^{-1}.$ Den exakta definitionen varierar: den definieras ibland som volymen av en sfär med radien $cH_{0}^{-1},$ eller alternativt en kub av sidan $cH_{0}^{-1}.$ Vissa kosmologer använder till och med termen Hubble-volym för att hänvisa till volymen av det observerbara universum , även om denna har en radie som är ungefär tre gånger större.

Bestämning av Hubble-konstanten

Värde på Hubble-konstanten, inklusive mätosäkerhet för de senaste undersökningarna

Värdet på Hubble-konstanten uppskattas genom att mäta rödförskjutningen av avlägsna galaxer och sedan bestämma avstånden till dem med någon annan metod än Hubbles lag. Detta tillvägagångssätt utgör en del av den kosmiska avståndsstegen för att mäta avstånd till extragalaktiska objekt. Osäkerheter i de fysiska antaganden som används för att bestämma dessa avstånd har orsakat varierande uppskattningar av Hubble-konstanten.

Hubble-spänning

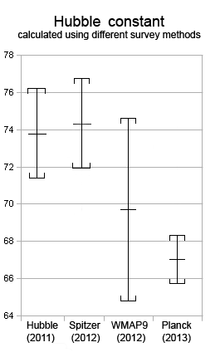
Flera metoder har använts för att bestämma Hubble-konstanten. "Sent universum"-mätningar med hjälp av kalibrerade distansstegetekniker har konvergerat till ett värde på cirka 73 (km/s)/Mpc . Sedan 2000 har "tidiga universum"-tekniker baserade på mätningar av den kosmiska mikrovågsbakgrunden blivit tillgängliga, och dessa är överens om ett värde nära 67,7 (km/s)/Mpc . (Detta står för förändringen i expansionshastigheten sedan det tidiga universum, så den är jämförbar med den första siffran.) Allt eftersom teknikerna har förbättrats har de uppskattade mätosäkerheterna minskat, men intervallet för uppmätta värden har inte, till den grad att oenigheten är nu mycket statistiskt signifikant . Denna diskrepans kallas Hubble-spänningen.

I december 2021 rapporterade National Geographic att orsaken till Hubble-spänningsskillnaden inte är känd. Men om den kosmologiska principen misslyckas (se " Brott mot den kosmologiska principen " i artikeln " Lambda-CDM-modellen "), måste de befintliga tolkningarna av Hubble-konstanten och Hubble-spänningen revideras, vilket kan lösa Hubble-spänningen .

En möjlighet är att Hubble-spänningen orsakas av KBC Void , eftersom mätning av galaktiska supernovor inuti ett tomrum förutsägs av vissa författare att ge ett större lokalt värde för Hubble-konstanten än kosmologiska mått på Hubble-konstanten. Andra arbeten har dock inte hittat några bevis för detta i observationer, och finner att skalan av den påstådda underdensiteten är oförenlig med observationer som sträcker sig utanför dess radie. Viktiga brister påpekades senare i denna analys, vilket lämnade möjligheten öppen att Hubble-spänningen verkligen orsakas av utflöde från KBC Void.

En annan möjlighet är att Hubble-spänningen kräver ny fysik utöver ΛCDM-modellen. Moritz Haslbauer och medarbetare har föreslagit modifierad newtonsk dynamik som en möjlig lösning på Hubble-spänningen, medan Marc Kamionkowski och medarbetare har föreslagit en tidig mörk energimodell som en möjlig lösning på Hubble-spänningen. Andra har föreslagit att åtminstone en del av spänningen kan vara ett resultat av underskattning av osäkerheter i data.

Tidigare mät- och diskussionssätt

Observationerna av astronomen Walter Baade fick honom att definiera distinkta " populationer " för stjärnor (befolkning I och befolkning II). Samma observationer fick honom att upptäcka att det finns två typer av Cepheid variabla stjärnor. Med hjälp av denna upptäckt räknade han om storleken på det kända universum, vilket fördubblade den tidigare beräkningen som Hubble gjorde 1929. Han tillkännagav detta fynd till stor förvåning vid Internationella astronomiska unionens möte 1952 i Rom.

uppskattades värdet på ${\displaystyle H_{0}} till mellan 50 och$ 90 (km/s)/Mpc .

Värdet på Hubble-konstanten var ämnet för en lång och ganska bitter kontrovers mellan Gérard de Vaucouleurs , som hävdade att värdet var runt 100, och Allan Sandage , som hävdade att värdet var nära 50. I en demonstration av vitriol som delas mellan parterna , när Sandage och Gustav Andreas Tammann (Sandages forskarkollega) formellt erkände bristerna i att bekräfta det systematiska felet i deras metod 1975, svarade Vaucouleurs "Det är olyckligt att denna nyktra varning så snart glömdes och ignorerades av de flesta astronomer och läroboksförfattare" . 1996 hölls en debatt moderaterad av John Bahcall mellan Sidney van den Bergh och Gustav Tammann på liknande sätt som den tidigare Shapley-Curtis-debatten om dessa två konkurrerande värderingar.

Denna tidigare stora variation i uppskattningar löstes delvis med introduktionen av ΛCDM-modellen av universum i slutet av 1990-talet. Med ΛCDM-modellobservationer av kluster med hög rödförskjutning vid röntgen- och mikrovågsvåglängder med Sunyaev-Zel'dovich-effekten, gav mätningar av anisotropier i den kosmiska mikrovågsbakgrundsstrålningen och optiska undersökningar ett värde på runt 70 för konstanten.

2000-talets mätningar

Landskap av H0-mätningar runt 2021 med Planck (2018) och SH0ES (2020) värden markerade i rosa respektive cyan.

Nyare mätningar från Planck-uppdraget som publicerades 2018 indikerar ett lägre värde på 67,66 ± 0,42 (km/s)/Mpc, även om, ännu mer nyligen, i mars 2019, ett högre värde på 74,03 ± 1,42 (km/s)/Mpc har fastställts med hjälp av en förbättrad procedur som involverar rymdteleskopet Hubble. De två mätningarna stämmer inte överens på 4,4 σ -nivån, bortom en rimlig risknivå. Lösningen på denna oenighet är ett pågående område av aktiv forskning.

I oktober 2018 presenterade forskare ett nytt tredje sätt (två tidigare metoder, en baserad på rödförskjutningar och en annan på den kosmiska avståndsstegen, gav resultat som inte överensstämmer), med hjälp av information från gravitationsvåghändelser (särskilt de som involverar sammanslagning av neutronstjärnor , som GW170817 ), för att bestämma Hubble-konstanten.

I juli 2019 rapporterade astronomer att en ny metod för att bestämma Hubble-konstanten och lösa diskrepansen mellan tidigare metoder, har föreslagits baserat på sammanslagningar av par av neutronstjärnor, efter upptäckten av neutronstjärnans sammanslagning av GW170817, en händelse känd som en mörk siren . Deras mätning av Hubble-konstanten är 73,3
+5,3 −5,0 (km/s)/Mpc.

Även i juli 2019 rapporterade astronomer en annan ny metod, med hjälp av data från rymdteleskopet Hubble och baserat på avstånd till röda jättestjärnor beräknade med spetsen på avståndsindikatorn för den röda jättegrenen (TRGB). Deras mätning av Hubble-konstanten är 69,8
+1,9 −1,9 (km/s)/Mpc.

I februari 2020 publicerade Megamaser Cosmology Project oberoende resultat som bekräftade distansstegeresultaten och skilde sig från resultaten från tidiga universum med en statistisk signifikansnivå på 95 %. I juli 2020 förutspår mätningar av den kosmiska bakgrundsstrålningen från Atacama Cosmology Telescope att universum bör expandera långsammare än vad som för närvarande observeras.

Uppskattade värden för Hubble-konstanten, 2001–2020. Uppskattningar i svart representerar kalibrerade distansstegemått som tenderar att samlas runt 73 (km/s)/Mpc ; rött representerar tidiga CMB/BAO-mätningar i universum med ΛCDM-parametrar som visar god överensstämmelse på en siffra nära 67 (km/s)/Mpc , medan blå är andra tekniker, vars osäkerheter ännu inte är tillräckligt små för att avgöra mellan de två.

Mätning av Hubble-konstanten

Publiceringsdatum	Hubble konstant (km/s)/Mpc	Observatör	Citat	Anmärkningar / metodik
2022-12-12	68,3 ± 1,5	SPT-3G		CMB TT/TE/EE effektspektrum. Mindre än 1 σ avvikelse med planck. (Förtryck)
2022-02-08	73,4 +0,99 −1,22	Pantheon+		SN Ia distansstege (+SH0ES)
2021-12-08	73,04 ± 1,04	SH0ES		Cepheider - SN Ia distansstege (HST+ Gaia EDR3 +"Pantheon+"). 5 σ avvikelse med planck.
2021-09-17	69,8 ± 1,7	W. Freedman		Spetsen på den röda jättegrenens (TRGB) avståndsindikator (HST+Gaia EDR3)
2020-12-16	72,1 ± 2,0	Rymdteleskopet Hubble och Gaia EDR3		Kombinera tidigare arbete på röda jättestjärnor , med spetsen på avståndsindikatorn för den röda jättegrenen (TRGB), med parallaxmätningar av Omega Centauri från Gaia EDR3.
2020-12-15	73,2 ± 1,3	Rymdteleskopet Hubble och Gaia EDR3		Kombination av HST- fotometri och Gaia EDR3-parallaxer för Vintergatans Cepheider , vilket minskar osäkerheten i kalibreringen av Cepheidens ljusstyrka till 1,0 %. Den totala osäkerheten i värdet för $H_{0}$ är 1,8 %, vilket förväntas minska till 1,3 % med ett större urval av supernovor av typ Ia i galaxer som är kända Cepheidvärdar. Fortsättning på ett samarbete känt som Supernovae, $H_{0}$ , för Equation of State of Dark Energy (SHoES).
2020-12-04	73,5 ± 5,3	EJ Baxter, BD Sherwin		Gravitationslinser i CMB används för att uppskatta $H_{0}$ utan att hänvisa till ljudhorisontskalan, vilket ger en alternativ metod för att analysera Planck - data.
2020-11-25	71,8 +3,9 −3,3	P. Denzel et al.		Åtta galaxsystem med fyrdubbla linser används för att bestämma $H_{0}$ med en precision på 5 %, i överensstämmelse med både "tidiga" och "sena" universums uppskattningar. Oberoende av distansstegar och den kosmiska mikrovågsbakgrunden.
2020-11-07	67,4 ± 1,0	T. Sedgwick et al.		Härledd från 88 0,02 < $z$ < 0,05 Supernovor av typ Ia som används som standardljusavståndsindikatorer. H ${\displaystyle H_{0}} -uppskattningen är korrigerad för effekterna av speciella hastigheter i supernovamiljöerna, som$ från galaxdensitetsfältet. Resultatet antar Ω m = 0,3, Ω Λ = 0,7 och en ljudhorisont på 149,3 Mpc, ett värde hämtat från Anderson et al. (2014).
2020-09-29	67,6 +4,3 −4,2	S. Mukherjee et al.		Gravitationsvågor , förutsatt att den transienta ZTF19abanrh som hittats av Zwicky Transient Facility är den optiska motsvarigheten till GW190521 . Oberoende av distansstegar och den kosmiska mikrovågsbakgrunden.
2020-06-18	75,8 +5,2 −4,9	T. de Jaeger et al.		Använd supernovor av typ II som standardiserbara ljus för att få en oberoende mätning av Hubble-konstanten—7 SNe II med värd-galaxavstånd uppmätta från Cepheidvariabler eller spetsen på den röda jättegrenen—
2020-02-26	73,9 ± 3,0	Megamaser kosmologiprojekt		Geometriska avståndsmätningar till megamaservärdiga galaxer. Oberoende av distansstegar och den kosmiska mikrovågsbakgrunden.
2019-10-14	74,2 +2,7 -3,0	FRAMGÅNG		Modellering av massfördelningen och tidsfördröjningen för den linsförsedda kvasaren DES J0408-5354.
2019-09-12	76,8 ± 2,6	SHARP/H0LiCOW		Modellera tre galaktiskt linsförsedda objekt och deras linser med hjälp av markbaserad adaptiv optik och Hubble Space Telescope.
2019-08-20	73,3 +1,36 −1,35	K. Dutta et al.		Denna $H_{0}$ erhålls genom att analysera kosmologiska data med låg rödförskjutning inom ΛCDM-modellen. Datauppsättningarna som används är supernovor av typ Ia, akustiska baryonoscillationer , tidsfördröjningsmätningar med stark linsning, ${\displaystyle H(z)}-$ mätningar med kosmiska kronometrar och tillväxtmätningar från storskaliga strukturobservationer.
2019-08-15	73,5 ± 1,4	MJ Reid, DW Pesce, AG Riess		Mätning av avståndet till Messier 106 med hjälp av dess supermassiva svarta hål, kombinerat med mätningar av förmörkande binärer i det stora magellanska molnet.
2019-07-16	69,8 ± 1,9	Hubble rymdteleskop		Avstånd till röda jättestjärnor beräknas med spetsen på avståndsindikatorn för den röda jättegrenen (TRGB).
2019-07-10	73,3 +1,7 −1,8	H0LiCOW-samarbete		Uppdaterade observationer av flerbildsbildade kvasarer, nu med sex kvasarer, oberoende av den kosmiska avståndsstegen och oberoende av de kosmiska mikrovågsbakgrundsmätningarna.
2019-07-08	70,3 +5,3 -5,0	LIGO och Jungfru detektorer		Använder radiomotsvarighet till GW170817 , kombinerat med tidigare gravitationsvåg (GW) och elektromagnetisk (EM) data.
2019-03-28	68,0 +4,2 -4,1	Fermi-LAT		Gammastrålningsdämpning på grund av extragalaktiskt ljus. Oberoende av den kosmiska avståndsstegen och den kosmiska mikrovågsbakgrunden.
2019-03-18	74,03 ± 1,42	Hubble rymdteleskop		Precisions-HST-fotometri av cepheider i det stora magellanska molnet (LMC) minskar osäkerheten i avståndet till LMC från 2,5 % till 1,3 %. Revideringen ökar spänningen med CMB- mätningar till 4,4 σ -nivån (P=99,999 % för Gaussiska fel), vilket ökar avvikelsen bortom en rimlig risknivå. Fortsättning på ett samarbete känt som Supernovae, $H_{0}$ , för Equation of State of Dark Energy (SHoES).
2019-02-08	67,78 +0,91 -0,87	Joseph Ryan et al.		Quasar vinkelstorlek och baryon akustiska svängningar, förutsatt att en platt ΛCDM modell. Alternativa modeller resulterar i olika (generellt lägre) värden för Hubble-konstanten.
2018-11-06	67,77 ± 1,30	Dark Energy Survey		Supernovamätningar med den omvända distansstegemetoden baserad på akustiska baryonsvängningar.
2018-09-05	72,5 +2,1 -2,3	H0LiCOW-samarbete		Observationer av flerbildsbildade kvasarer, oberoende av den kosmiska avståndsstegen och oberoende av de kosmiska mikrovågsbakgrundsmätningarna.
2018-07-18	67,66 ± 0,42	Planck uppdrag		Final Planck 2018 resultat.
2018-04-27	73,52 ± 1,62	Rymdteleskopet Hubble och Gaia		Ytterligare HST- fotometri av galaktiska Cepheider med tidiga Gaia-parallaxmätningar. Det reviderade värdet ökar spänningen med CMB- mätningar på 3,8 σ -nivån. Fortsättning på SHoES-samarbetet.
2018-02-22	73,45 ± 1,66	Hubble rymdteleskop		Parallaxmätningar av galaktiska cepheider för förbättrad kalibrering av distansstegen ; värdet antyder en diskrepans med CMB-mätningar på 3,7 σ -nivån. Osäkerheten förväntas minska till under 1 % i och med den slutliga releasen av Gaia-katalogen. SKO samarbete.
2017-10-16	70,0 +12,0 -8,0	LIGO Scientific Collaboration och The Virgo Collaboration		Standard sirenmätning oberoende av normala "standardljus"-tekniker; gravitationsvågsanalysen av en binär neutronstjärna (BNS) sammanslagning GW170817 uppskattade direkt ljusstyrkans avstånd ut till kosmologiska skalor. En uppskattning av femtio liknande upptäckter under det kommande decenniet kan medföra spänningar mellan andra metoder. Detektering och analys av en neutronstjärna-svarthålsfusion (NSBH) kan ge större precision än vad BNS skulle kunna tillåta.
2016-11-22	71,9 +2,4 -3,0	Hubble rymdteleskop		Använder tidsfördröjningar mellan flera bilder av avlägsna variabla källor producerade av stark gravitationslins . Samarbete känd som $H_{0}$ -linser i COSMOGRAIL's Wellspring (H0LiCOW).
2016-08-04	76,2 +3,4 −2,7	Kosmiska flöden-3		Jämför rödförskjutning med andra avståndsmetoder, inklusive Tully-Fisher , Cepheid-variabel och Type Ia-supernovor. En restriktiv uppskattning från data innebär ett mer exakt värde på 75 ± 2 .
2016-07-13	67,6 +0,7 -0,6	SDSS-III Baryon Oscillation Spectroscopic Survey (BOSS)		Baryon akustiska svängningar. En utökad undersökning (eBOSS) påbörjades 2014 och förväntas pågå till och med 2020. Den utökade undersökningen är utformad för att utforska tiden då universum höll på att övergå från gravitationens retardationseffekter från 3 till 8 miljarder år efter Big Bang.
2016-05-17	73,24 ± 1,74	Hubble rymdteleskop		Typ Ia supernova , osäkerheten förväntas minska med en faktor på mer än två med kommande Gaia-mätningar och andra förbättringar. SKO samarbete.
2015-02	67,74 ± 0,46	Planck uppdrag		Resultat från en analys av Plancks fullständiga uppdrag offentliggjordes den 1 december 2014 vid en konferens i Ferrara , Italien. En fullständig uppsättning papper som beskriver uppdragets resultat släpptes i februari 2015.
2013-10-01	74,4 ± 3,0	Kosmiska flöden-2		Jämför rödförskjutning med andra avståndsmetoder, inklusive Tully-Fisher, Cepheid-variabel och Type Ia-supernovor.
2013-03-21	67,80 ± 0,77	Planck uppdrag		ESA Planck Surveyor lanserades i maj 2009. Under en fyraårsperiod utförde den en betydligt mer detaljerad undersökning av kosmisk mikrovågsstrålning än tidigare undersökningar med HEMT - radiometrar och bolometerteknik för att mäta CMB i mindre skala än WMAP. Den 21 mars 2013 släppte det europeiskt ledda forskarteamet bakom Planck kosmologisonden uppdragets data inklusive en ny CMB all-sky-karta och deras bestämning av Hubble-konstanten.
2012-12-20	69,32 ± 0,80	WMAP (9 år), kombinerat med andra mätningar.
2010	70,4 +1,3 −1,4	WMAP (7 år), kombinerat med andra mätningar.		0 Dessa värden uppstår från att anpassa en kombination av WMAP och andra kosmologiska data till den enklaste versionen av ΛCDM-modellen. Om data passar mer generella versioner, H att vara mindre och mer osäker: vanligtvis runt 67 ± 4 (km/s)/Mpc även om vissa modeller tillåter värden nära 63 (km/s)/Mpc .
2010	71,0 ± 2,5	Endast WMAP (7 år).
2009-02	70,5 ± 1,3	WMAP (5 år), kombinerat med andra mätningar.
2009-02	71,9 +2,6 −2,7	Endast WMAP (5 år)
2007	70,4 +1,5 −1,6	WMAP (3 år), kombinerat med andra mätningar.
2006-08	76,9 +10,7 −8,7	Chandra röntgenobservatorium		Kombinerad Sunyaev-Zeldovich-effekt och Chandra-röntgenobservationer av galaxhopar . Justerad osäkerhet i tabell från Planck Collaboration 2013.
2003	72 ± 5	Endast WMAP (första året).	.
2001-05	72 ± 8	Hubble rymdteleskop nyckelprojekt		0 Detta projekt etablerade den mest exakta optiska bestämningen, i överensstämmelse med en mätning av H baserat på Sunyaev–Zel'dovich effektobservationer av många galaxhopar med liknande noggrannhet.
före 1996	50–90 (uppskattning)
1994	67 ± 7	Supernova 1a ljuskurvformer		Bestämt förhållande mellan ljusstyrkan hos SN 1a och deras ljuskurvformer. Riess et al använde detta förhållande mellan ljuskurvan för SN 1972E och Cepheidavståndet till NGC 5253 för att bestämma konstanten.
mitten av 1970-talet	100 ± 10	Gérard de Vaucouleurs		De Vaucouleurs trodde att han hade förbättrat noggrannheten hos Hubbles konstant från Sandages eftersom han använde 5 gånger fler primära indikatorer, 10 gånger fler kalibreringsmetoder, 2 gånger fler sekundära indikatorer och 3 gånger så många galaxdatapunkter för att härleda sina 100 ± 10.
tidigt 1970-tal	≈ 55 (uppskattning)	Allan Sandage och Gustav Tammann
1958	75 (uppskattat)	Allan Sandage		0 Detta var den första bra uppskattningen av H , men det skulle dröja årtionden innan en konsensus uppnåddes.
1956	180	Humason , Mayall och Sandage
1929	500	Edwin Hubble , Hooker-teleskop
1927	625	Georges Lemaître		Första mätningen och tolkningen som ett tecken på universums expansion

Se även

• Accelererande expansion av universum
• Kosmologi
• Mörk materia
• Tester av allmän relativitet

Bibliografi

•   Hubble, EP (1937). Den observationella inställningen till kosmologi . Clarendon Press . LCCN 38011865 .
•   Kutner, M. (2003). Astronomi: ett fysiskt perspektiv . Cambridge University Press . ISBN 978-0-521-52927-3 .
•   Liddle, AR (2003). An Introduction to Modern Cosmology (2nd ed.). John Wiley & Sons . ISBN 978-0-470-84835-7 .

Vidare läsning

•   Freedman, WL; Madore, BF (2010). "The Hubble Constant". Årlig översyn av astronomi och astrofysik . 48 : 673-710. arXiv : 1004.1856 . Bibcode : 2010ARA&A..48..673F . doi : 10.1146/annurev-astro-082708-101829 . S2CID 119263173 .

externa länkar

• NASA:s WMAP - Big Bang Expansion: the Hubble Constant
• Hubble Key-projektet
• Hubble Diagram-projektet
• Att komma överens med olika Hubble-konstanter ( Forbes ; 3 maj 2019)
• Merrifield, Michael (2009). "Hubbles konstant" . Sextio symboler . Brady Haran för University of Nottingham .