Holonomiska begränsningar

I klassisk mekanik är holonomiska begränsningar relationer mellan positionsvariablerna (och möjligen tid) som kan uttryckas i följande form :

f(u_{1},u_{2},u_{3},\ldots ,u_{n},t)= 0

där $\{u_{1},u_{2},u_{3},\ldots ,u_{n}\}$ är n generaliserade koordinater som beskriver systemet (i obegränsat konfigurationsutrymme ). Till exempel är rörelsen hos en partikel som är begränsad att ligga på ytan av en sfär föremål för en holonomisk begränsning, men om partikeln kan falla av sfären under påverkan av gravitationen blir begränsningen icke-holonomisk. För det första fallet kan den holonomiska begränsningen ges av ekvationen

r^{2}-a^{2}=0

där $r$ är avståndet från mitten av en sfär med radie $a$ , medan det andra icke-holonomiska fallet kan ges av

r^{2}-a^{2}\geq 0

Hastighetsberoende begränsningar (även kallade semi-holonomiska begränsningar) som t.ex

f(u_{1},u_{2},\ldots ,u_{ n},{\dot {u}}_{1},{\dot {u}}_{2},\ldots,{\dot {u}}_{n},t)=0

är vanligtvis inte holonomiska. ^{[ citat behövs ]}

Holonomiskt system

I klassisk mekanik kan ett system definieras som holonomiskt om alla begränsningar i systemet är holonomiska. För att en begränsning ska vara holonomisk måste den kunna uttryckas som en funktion :

f(u_{1},\ u_{2},\ u_{3},\ \ldots ,\ u_{n },\ t)=0,\,

dvs en holonomisk begränsning beror bara på koordinaterna $x_{j}$ och kanske tiden $t$ . Det beror inte på hastigheterna eller någon högre ordningsderivata med avseende på t . En begränsning som inte kan uttryckas i formen som visas ovan är en icke-holonomisk begränsning .

Introduktion

Som beskrivits ovan är ett holonomiskt system (enkelt talat) ett system där man kan härleda tillståndet för ett system genom att bara veta förändringen av positionerna för komponenterna i systemet över tid, men inte behöva veta hastigheten eller i vilken beställa komponenterna flyttade i förhållande till varandra. Däremot är ett icke-holonomiskt system ofta ett system där komponenternas hastigheter över tid måste vara kända för att kunna bestämma tillståndsändringen i systemet, eller ett system där en rörlig del inte kan bindas till en begränsning yta, verklig eller imaginär. Exempel på holonomiska system är portalkranar, pendlar och robotarmar. Exempel på icke-holonomiska system är Segways , enhjulingar och bilar.

Terminologi

Konfigurationsutrymmet ${\overrightarrow {u}}$ listar förskjutningen av komponenterna i systemet, en för varje frihetsgrad . Ett system som kan beskrivas med hjälp av ett konfigurationsutrymme kallas skleronomiskt .

{\overrightarrow {u}}={\begin{bmatrix}u_{1}&u_{2}&\ldots &u_{n}\end{bmatrix} }^{\mathrm {T} }

Händelseutrymmet är identiskt med konfigurationsutrymmet förutom tillägget av en variabel $t$ för att representera förändringen i systemet över tid (om det behövs för att beskriva systemet). Ett system som måste beskrivas med ett händelseutrymme, istället för endast ett konfigurationsutrymme, kallas rheonomic . Många system kan beskrivas antingen skleronomiskt eller reonomiskt. Till exempel kan den totala tillåtna rörelsen för en pendel beskrivas med en skleronomisk begränsning, men rörelsen över tiden av en pendel måste beskrivas med en reonomisk begränsning.

{\overrightarrow {u}}={\begin{bmatrix}u_{1}&u_{2}&\ldots &u_{n}&t\end{ bmatrix}}^{\mathrm {T} }

Tillståndsutrymmet ${\overrightarrow {q}}$ är konfigurationsutrymmet, plus termer som beskriver hastigheten för varje term i konfigurationsutrymmet .

{\overrightarrow {q}}={\begin{bmatrix}{\overrightarrow {u}} \\{\overrightarrow {\dot {u}}}\end{bmatrix}}={\begin{bmatrix}u_{1}&\ldots &u_{n}&{\dot {u}}_{1}& \ldots &{\dot {u}}_{n}\end{bmatrix}}^{\mathrm {T} }

Tillstånd -tidsutrymmet lägger till tid $t$ .

{\overrightarrow {q}}={\begin{bmatrix}{\overrightarrow {u} }\\{\overrightarrow {\dot {u}}}\end{bmatrix}}={\begin{bmatrix}u_{1}&\ldots &u_{n}&t&{\dot {u}}_{1} &\ldots &{\dot {u}}_{n}\end{bmatrix}}^{\mathrm {T} }

Exempel

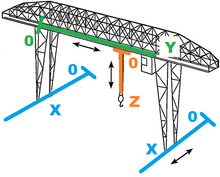
Gantry kran

En bild av en portalkran, med markerade yxor

Som visas till höger är en portalkran en travers som kan flytta sin krok i 3 axlar enligt pilarna. Intuitivt kan vi härleda att kranen bör vara ett holonomiskt system eftersom det för en given rörelse av dess komponenter inte spelar någon roll vilken ordning eller hastighet komponenterna rör sig: så länge som den totala förskjutningen av varje komponent från ett givet starttillstånd är samma, kommer alla delar och systemet som helhet att hamna i samma tillstånd. Matematiskt kan vi bevisa detta som sådant:

Vi kan definiera systemets konfigurationsutrymme som:

{\overrightarrow {u}}={\begin{bmatrix}x\\y\\z\end{bmatrix}}

Vi kan säga att avböjningen av varje komponent i kranen från dess "noll"-läge är $B$ , $G$ och $O$ , för de blå, gröna och orangea komponenterna , respektive. Orienteringen och placeringen av koordinatsystemet spelar ingen roll om ett system är holonomiskt, men i detta exempel råkar komponenterna röra sig parallellt med dess axlar. Om ursprunget för koordinatsystemet är längst bak nere till vänster på kranen, kan vi skriva positionsbegränsningsekvationen som:

(xB)+(yG)+(z-(hO))=0

Där $h$ är höjden på kranen. Alternativt kan vi förenkla till standardformen där alla konstanter placeras efter variablerna:

x+y+z-(B+G+hO)=0

Eftersom vi har härlett en begränsningsekvation i holonomisk form (specifikt har vår begränsningsekvation formen $f(x,y,z)=0$ där ${\displaystyle \{x,y,z\}\in {\overrightarrow {u}}} )$ , kan vi se att detta system måste vara holonomiskt.

Pendel

En enkel pendel

Som visas till höger är en enkel pendel ett system som består av en vikt och ett snöre. Snöret är fäst i den övre änden till en pivot och i den nedre änden till en vikt. Eftersom strängen är outtöjbar är längden konstant. Detta system är holonomiskt eftersom det följer den holonomiska begränsningen

{x^{2}+y^{2}}-L^{2}=0,

där $(x,\ y)$ är viktens position och $L$ är längden på strängen.

Stel kropp

Partiklarna i en stel kropp lyder den holonomiska begränsningen

(\mathbf {r} _{i}-\mathbf {r} _{j})^{2}-L_{ij}^{ 2}=0,\,

där $\mathbf {r} _{i}$ , $\mathbf {r} _{j}$ är positionerna för partiklarna $P_{i}$ respektive $P_{j}$ , och $L_{ij}$ är avståndet mellan dem. Om ett givet system är holonomiskt kan det inte göra det icke-holonomiskt att stela ytterligare delar till komponenterna i det aktuella systemet, förutsatt att frihetsgraderna inte reduceras (med andra ord, förutsatt att konfigurationsutrymmet är oförändrat).

Pfaffisk form

Tänk på följande differentialform av en begränsning:

\sum _{j}\ A_{ij}\,du_{j}+A_{i}\,dt=0

där $A_{ij},A_{i}$ är koefficienterna för differentialerna $du_{j},dt$ för den i: te begränsningsekvationen. Denna form kallas den pfaffiska formen eller differentialformen .

Om differentialformen är integrerbar, dvs. om det finns en funktion ${\displaystyle f_{i}(u_{1},\ u_{ 2},\ u_{3},\ \ldots ,\ u_{n},\ t)=0} som$ uppfyller jämställdheten

df_{i}=\summa _{j}\ A_{ij}\,du_{j}+A_{i}\, dt=0

då är denna begränsning en holonomisk begränsning; annars är den icke-holonomisk. Därför kan alla holonomiska och vissa icke-holonomiska begränsningar uttryckas med hjälp av differentialformen. Exempel på icke-holonomiska begränsningar som inte kan uttryckas på detta sätt är de som är beroende av generaliserade hastigheter. ^{[ förtydligande behövs ]} Med en begränsningsekvation i Pfaffisk form, beror om begränsningen är holonomisk eller icke-holonomisk på om den Pfaffiska formen är integrerbar. Se Universellt test för holonomiska begränsningar nedan för en beskrivning av ett test för att verifiera integrerbarheten (eller bristen på) av en Pfaffisk formbegränsning.

Universellt test för holonomiska begränsningar

När begränsningsekvationen för ett system skrivs i Pfaffisk begränsningsform, finns det ett matematiskt test för att avgöra om systemet är holonomiskt.

För en begränsningsekvation, eller $i$ uppsättningar av begränsningsekvationer (observera att variabel(er) som representerar tid kan inkluderas, från ovan $A_{i}\in A_{ij }$ och $\,dt\in du_{j}$ i följande form):

\sum _{j}^{n}\ A_{ij}\,du_{j}=0;\,

vi kan använda testekvationen:

A_{\gamma }\left({\frac {\partial A_{\beta }}{\partial u_{\alpha }}}-{\frac {\partial A_{\alpha }} {\partial u_{\beta }}}\right)+A_{\beta}\left({\frac {\partial A_{\alpha }}{\partial u_{\gamma }}}-{\frac {\ partiell A_{\gamma }}{\partial u_{\alpha }}}\right)+A_{\alpha }\left({\frac {\partial A_{\gamma }}{\partial u_{\beta }} }-{\frac {\partial A_{\beta }}{\partial u_{\gamma }}}\right)=0

var

\alpha ,\beta ,\gamma =1,2,3\ldots n

in

{\textstyle {\binom {n}{3}}={\frac {n(n-1)(n-2)}{6 }}}

kombinationer av testekvationer per begränsningsekvation, för alla

i

uppsättningar av begränsningsekvationer.

Med andra ord skulle ett system med tre variabler behöva testas en gång med en testekvation där termerna $\alpha ,\beta ,\gamma$ är termerna $1 ,2,3$ i begränsningsekvationen (i valfri ordning), men för att testa ett system med fyra variabler måste testet utföras upp till fyra gånger med fyra olika testekvationer, med termerna ${\ displaystyle \alpha ,\beta ,\gamma }$ är termerna $1,2,3$ , $1,2,4$ , $1,3,4$ , och $2,3,4$ i begränsningsekvationen (var och en i valfri ordning) i fyra olika tester. För ett system med fem variabler, tio tester behöva utföras på ett holonomiskt system för att verifiera detta faktum, och för ett system med fem variabler med tre uppsättningar av begränsningsekvationer, trettio test (om man antar en förenkling som en förändring av variabel kunde inte utföras för att minska det antalet). Av denna anledning är det lämpligt att när man använder den här metoden på system med fler än tre variabler använda sunt förnuft om huruvida systemet i fråga är holonomiskt, och bara fortsätta testa om systemet sannolikt inte är det. Dessutom är det också bäst att använda matematisk intuition för att försöka förutsäga vilket test som skulle misslyckas först och börja med det, och hoppa över tester som till en början verkar lyckas.

Om varje testekvation är sann för hela uppsättningen av kombinationer för alla begränsningsekvationer, är systemet holonomiskt. Om det är osant för ens en testkombination är systemet icke-holonomiskt.

Exempel

Betrakta detta dynamiska system som beskrivs av en begränsningsekvation i Pfaffisk form.

(\cos \theta )dx+(\sin \theta )dy+(y\ cos \theta -x\sin \theta )d\theta =0

Konfigurationsutrymmet, genom inspektion, är ${\overrightarrow {u}}={\begin{bmatrix}x&y&\theta \end{bmatrix}}^{\mathrm {T} }$ . Eftersom det bara finns tre termer i konfigurationsutrymmet kommer det bara att behövas en testekvation. Vi kan organisera termerna för begränsningsekvationen som sådana, som förberedelse för substitution:

A_{\alpha }=\cos \theta

A_{\beta }=\sin \theta

A_{\gamma }=y\cos \theta -x\sin \theta

u_{\alpha }=dx

u_{\ beta }=dy

u_{\gamma }=d\theta

Genom att ersätta termerna blir vår testekvation:

θ \theta -x\sin \theta ){\bigg (}{\frac {\partial }{\partial x}}(\sin \theta )-{\frac {\partial }{\partial y}}(\cos \theta ){\bigg )}+(\sin \theta ){\bigg (}{\frac {\partial }{\partial \theta }}(\cos \theta )-{\frac {\partial }{\ partiell x}}(y\cos \theta -x\sin \theta ){\bigg )}+(\cos \theta ){\bigg (}{\frac {\partial }{\partial y}}(y\ cos \theta -x\sin \theta )-{\frac {\partial }{\partial \theta }}(\sin \theta ){\bigg )}=0}

Efter att ha beräknat alla partiella derivator får vi:

_ \displaystyle (y\cos \theta -x\sin \theta ){\bigg (}0-0{\bigg )}+(\sin \theta){\bigg (}-\sin \theta -(-\sin \theta ){\bigg )}+(\cos \theta ){\bigg (}\cos \theta -\cos \theta {\bigg )}=0}

Förenklat finner vi att:

0=0

Vi ser att vår testekvation är sann, och därför måste systemet vara holonomiskt.

Vi har avslutat vårt test, men nu när vi vet att systemet är holonomiskt, kanske vi vill hitta den holonomiska begränsningsekvationen. Vi kan försöka hitta det genom att integrera varje term i den Pfaffiska formen och försöka förena dem till en ekvation, som sådan:

\int (\cos \theta )dx=x\cos \theta +f(y,\theta )

\int (\sin \theta )dy=y\sin \theta +f(x,\theta )

\int (y\cos \theta -x\sin \theta )d\theta =y\sin \theta +x\cos \theta +f(x,y)

Det är lätt att se att vi kan kombinera resultaten av våra integrationer för att hitta den holonomiska begränsningsekvationen:

y\sin \theta +x\cos \theta +C=0

där C är integrationskonstanten.

Begränsningar av konstanta koefficienter

För en given Pfaffian begränsning där varje koefficient för varje differential är en konstant, med andra ord en begränsning i formen:

\sum _{j}\ A_{ij}\,du_{j}+A_{i}\,dt=0;\;\{A_{ij}, A_{i};\,j=1,2,\ldots ;\,i=1,2,\ldots \}\in \mathbb {R}

begränsningen måste vara holonomisk.

Vi kan bevisa detta enligt följande: betrakta ett system av begränsningar i Pfaffisk form där varje koefficient för varje differential är en konstant, som beskrivits direkt ovan. För att testa om detta system av begränsningar är holonomiskt använder vi det universella testet . Vi kan se att det i testekvationen finns tre termer som måste summeras till noll. Därför, om var och en av dessa tre termer i varje möjlig testekvation var och en är noll, så är alla testekvationer sanna och detta är systemet holonomiskt. Varje term i varje testekvation har formen:

A_{3}\left({\frac {\partial A_{2}}{\partial u_{1}}}-{\ frac {\partial A_{1}}{\partial u_{2}}}\right)

var:

$A_{1}$ , $A_{2}$ och $A_{3}$ är en kombination (med ${\textstyle {\binom {n}{3}}=n(n-1)(n-2)/6}$ totala kombinationer) av $A_{ij};\,j=1,2,\ldots$ och $A_{i}$ för en given begränsning $i$ .
$u_{1}$ , $u_{2}$ och $u_{3}$ är motsvarande kombination av $u_{j};\,j=1,2,\ldots$ och $dt$ .

Dessutom finns det $i$ uppsättningar av testekvationer.

Vi kan se att per definition alla $A_{n}$ är konstanter. Det är välkänt i kalkylen att varje derivata (hel eller partiell) av en konstant är { $\displaystyle 0}$ . Därför kan vi reducera varje partiell derivata till:

A_{3}{\big (}0-0{\big )}

och följaktligen är varje term noll, den vänstra sidan av varje testekvation är noll, varje testekvation är sann och systemet är holonomiskt.

Konfigurationsutrymmen med två eller en variabel

Alla system som kan beskrivas av en Pfaffian-begränsning och har ett konfigurationsutrymme eller tillståndsutrymme med endast två variabler eller en variabel är holonomiskt.

Vi kan bevisa detta som sådant: överväg ett dynamiskt system med ett konfigurationsutrymme eller tillståndsutrymme som beskrivs som:

{\overrightarrow {u}}={\begin{bmatrix}u_{1}&u_{2}\end{bmatrix}}^{\mathrm {T} }

om systemet beskrivs av ett tillståndsutrymme säger vi helt enkelt att $u_{2}$ är lika med vår tidsvariabel $t$ . Detta system kommer att beskrivas i Pfaffian form:

A_{i1}du_{1}+A_{i2}du_{2}=0

med $i$ uppsättningar av begränsningar. Systemet kommer att testas genom att använda det universella testet. Det universella testet kräver dock tre variabler i konfigurationen eller tillståndsutrymmet. För att tillgodose detta lägger vi helt enkelt till en dummyvariabel $\lambda$ till konfigurationen eller tillståndsutrymmet för att bilda:

{\overrightarrow {u}}={\begin{bmatrix}u_{1}&u_{2}&\lambda \end{bmatrix}}^{\mathrm { T} }

Eftersom dummyvariabeln $\lambda$ per definition inte är ett mått på något i systemet måste dess koefficient i Pfaffian-formen vara $0$ . Därför reviderar vi vår Pfaffiska form:

A_{i1}du_{1}+A_{i2}du_{2}+0d\lambda =0

Nu kan vi använda testet som sådant, för en given begränsning $i$ om det finns en uppsättning begränsningar:

(0){\bigg (}{\frac {\partial }{\partial u_{1}}}(A_{ i2})-{\frac {\partial }{\partial u_{2}}}(A_{i1}){\bigg )}+(A_{i2}){\bigg (}{\frac {\partial } {\partial \lambda }}(A_{i1})-{\frac {\partial }{\partial u_{1}}}(0){\bigg )}+(A_{i1}){\bigg (} {\frac {\partial }{\partial u_{2}}}(0)-{\frac {\partial }{\partial \lambda }}(A_{i2}){\bigg )}=0

När man inser att : ${\frac {\partial }{\partial \lambda }}(f(u_{1},u_{2}))= 0$ eftersom dummyvariabeln $\lambda$ inte kan förekomma i de koefficienter som används för att beskriva systemet, ser vi att testekvationen måste vara sann för alla uppsättningar av begränsningsekvationer och därför måste systemet vara holonomiskt. Ett liknande bevis kan utföras med en faktisk variabel i konfigurations- eller tillståndsutrymmet och två dummyvariabler för att bekräfta att system med en frihetsgrad som kan beskrivas i Pfaffisk form också alltid är holonomiska.

Sammanfattningsvis inser vi att även om det är möjligt att modellera icke-holonomiska system i Pfaffisk form, så är alla system som kan modelleras i Pfaffisk form med två eller färre frihetsgrader (antalet frihetsgrader är lika med antalet termer i konfigurationsutrymmet ) måste vara holonomisk.

Viktig anmärkning: inse att testekvationen misslyckades eftersom dummyvariabeln, och därmed dummydifferentialen som ingår i testet, kommer att differentiera allt som är en funktion av den faktiska konfigurationen eller tillståndsvariablerna till {\displaystyle 0 $}$ . Att ha ett system med en konfiguration eller ett tillståndsområde för:

{\overrightarrow {u}}={\begin{bmatrix}u_{1}&u_{2}&u_{3}\end{bmatrix}}^{\ mathrm {T} }

och en uppsättning begränsningar där en eller flera begränsningar är i Pfaffian form:

A_{i1}du_{1}+A_{i2}du_{2}+0du_{3}=0

garanterar inte att systemet är holonomiskt, eftersom även om en differential har en koefficient på $0$ finns det fortfarande tre frihetsgrader som beskrivs i konfigurationen eller tillståndsutrymmet.

Transformation till oberoende generaliserade koordinater

De holonomiska begränsningsekvationerna kan hjälpa oss att enkelt ta bort några av de beroende variablerna i vårt system. Om vi till exempel vill ta bort $x_{d}$ , som är en parameter i begränsningsekvationen $f_{i}$ , kan vi ordna om ekvationen till följande form, förutsatt att den kan bli gjort,

d}=g_{i}(x_{ 1},\ x_{2},\ x_{3},\ \dots ,\ x_{d-1},\ x_{d+1},\ \dots ,\ x_{N},\ t),\ ,}

och ersätt $x_{d}$ i varje ekvation i systemet med hjälp av ovanstående funktion. Detta kan alltid göras för allmänna fysiska system, förutsatt att derivatan av ${\displaystyle f_{i}} är kontinuerlig, då$ garanteras genom den implicita funktionssatsen , lösningen ${\displaystyle g_{i}} .$ i något öppet set. Således är det möjligt att ta bort alla förekomster av den beroende variabeln $x_{d}$ .

Antag att ett fysiskt system har $N$ frihetsgrader. Nu $h$ holonomiska begränsningar införda på systemet. Sedan reduceras antalet frihetsgrader till $m=Nh$ . Vi kan använda $m$ oberoende generaliserade koordinater ( ${\displaystyle q_{j}} )$ för att fullständigt beskriva systemets rörelse. Transformationsekvationen kan uttryckas på följande sätt:

x_{i}=x_{i}(q_{1},\ q_{2},\ \ldots ,\ q_{m},\ t)\ ,\qquad \qquad \qquad i=1,\ 2,\ \ldots N.\,

Klassificering av fysiska system

För att studera klassisk fysik rigoröst och metodiskt måste vi klassificera system. Baserat på tidigare diskussion kan vi klassificera fysiska system i holonomiska system och icke-holonomiska system . En av förutsättningarna för tillämpbarheten av många satser och ekvationer är att systemet måste vara ett holonomiskt system. Till exempel, om ett fysiskt system är ett holonomiskt system och ett monogent system , då är Hamiltons princip det nödvändiga och tillräckliga villkoret för riktigheten av Lagranges ekvation .

Se även