Herschel graf
| Herschel-graf | |
|---|---|
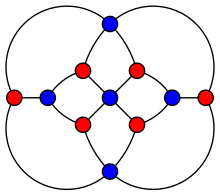 Herschel-grafen.
| |
| Döpt efter | Alexander Stewart Herschel |
| Vertices | 11 |
| Kanter | 18 |
| Automorfismer | 12 ( D 6 ) |
| Egenskaper | |
| Tabell över grafer och parametrar | |
I grafteorin , en gren av matematiken , är Herschel-grafen en tvådelad oriktad graf med 11 hörn och 18 kanter. Det är en polyedrisk graf (grafen av en konvex polyhedron ), och är den minsta polyedriska grafen som inte har en Hamiltonsk cykel , en cykel som passerar genom alla dess hörn. Den är uppkallad efter den brittiske astronomen Alexander Stewart Herschel , på grund av Herschels studier av Hamiltons cykler i polyedriska grafer (men inte av denna graf).
Definition och egenskaper
Herschel-grafen har tre hörn av grad fyra och åtta hörn av grad tre. Vart och ett av de tre paren av grad-fyra hörn bildar en cykel av fyra hörn, där de alternerar med två av de tre graders hörn. Var och en av de två återstående grad-tre hörnen ligger intill en grad-tre vertex från var och en av dessa tre cykler.
Herschel-grafen är en polyedrisk graf ; detta betyder att det är en plan graf , en som kan ritas i planet utan att någon av dess kanter korsar, och även 3-vertex-ansluten : borttagandet av två av dess hörn lämnar en ansluten subgraf . Det är en tvådelad graf : dess hörn kan separeras i två delmängder om fem respektive sex hörn, så att varje kant har en slutpunkt i varje delmängd (de röda och blå delmängderna i bilden).
Den har ordning-6 dihedral symmetri , för totalt 12 medlemmar av dess automorfismgrupp . Grad-fyra hörn kan permuteras godtyckligt, vilket ger sex permutationer, och dessutom, för varje permutation av grad-fyra hörn, finns det en symmetri som håller dessa hörn fixerade och utbyter par av grad-tre hörn.
Polyeder
Herschel-grafen är plan och 3-vertex-ansluten, så det följer av Steinitz sats att det är en polyedrisk graf : det finns en konvex polyeder (en enneahedron ) som har Herschel-grafen som sitt skelett . Denna polyeder har nio fyrhörningar för ansikten. Om dessa väljs så att polyedern har alla samma symmetrier som den underliggande grafen, kommer tre av ytorna att vara romber eller kvadrater, och de andra sex kommer att vara drakar .
Den dubbla polyedern är ett likriktat triangulärt prisma , som kan formas som det konvexa skrovet av mittpunkterna på kanterna på ett triangulärt prisma . När den är konstruerad på detta sätt har den tre fyrkantiga ytor på samma plan som prismats fyrkantiga ytor, två liksidiga triangelytor på planen för prismats triangulära ändar och ytterligare sex likbenta triangelytor. Denna polyeder har egenskapen att dess ytor inte kan numreras på ett sådant sätt att på varandra följande siffror visas på intilliggande ytor, och så att de första och sista siffrorna också finns på intilliggande ytor. Eftersom polyedriska ansiktsnumrering av denna typ används som "spindown life-räknare" i spelet Magic: The Gathering , kallar Constantinides & Constantinides (2018) den kanoniska polyhedronförverkligandet av denna dubbla polyeder som "the Lich's nemesis".
Hamiltonicitet
Som en tvådelad graf som har ett udda antal hörn, innehåller Herschel-grafen inte en Hamiltonsk cykel (en cykel av kanter som passerar genom varje vertex exakt en gång). För i alla tvådelade grafer måste varje cykel alternera mellan hörnen på vardera sidan av den tvådelade avdelningen och måste därför innehålla lika många av båda typerna av hörn och måste ha en jämn längd. Således kan en cykel som går en gång genom var och en av de elva hörnen inte existera i Herschel-grafen. Det är den minsta icke-Hamiltonska polyedriska grafen, oavsett om storleken på grafen mäts i termer av dess antal hörn, kanter eller ytor. Det finns andra polyedriska grafer med 11 hörn och inga Hamiltonska cykler (särskilt Goldner-Harary-grafen ) men ingen med färre kanter.
Alla utom tre hörn av Herschel-grafen har grad tre. Taits gissning säger att en polyedrisk graf där varje vertex har grad tre måste vara Hamiltonian, men detta motbevisades när WT Tutte gav ett motexempel, den mycket större Tutte-grafen . En förfining av Taits gissning, Barnettes gissning att varje tvådelad 3-regelbunden polyedrisk graf är Hamiltonsk, förblir öppen.
Varje maximal plan graf som inte har en Hamiltonsk cykel har en Herschel-graf som mindre . Herschel-grafen antas vara en av tre mindre-minimala, icke-Hamiltonska 3-vertex-anslutna grafer. De andra två är den kompletta tvådelade grafen och en graf som bildas genom att dela upp både Herschel-grafen och i två symmetriska halveras av separatorer med tre hörn och sedan kombinera en halva från varje graf.

Herschel-grafen ger också ett exempel på en polyedrisk graf för vilken den mediala grafen inte har någon Hamilton-nedbrytning i två Hamilton-cykler som skiljer sig från kanten. Den mediala grafen för Herschel-grafen är en 4- regelbunden graf med 18 hörn, en för varje kant av Herschel-grafen; två hörn är intill varandra i den mediala grafen närhelst motsvarande kanter på Herschel-grafen är konsekutiva på en av dess ytor. Den är 4-hörn-ansluten och i huvudsak 6-kant-ansluten , vilket betyder att för varje partition av hörnen i två delmängder av minst två hörn, finns det minst sex kanter som korsar partitionen.
Historia
Herschel-grafen är uppkallad efter den brittiske astronomen Alexander Stewart Herschel , som skrev en tidig artikel om William Rowan Hamiltons ikoniska spel : Herschel-grafen beskriver den minsta konvexa polyedern som detta spel inte har någon lösning på. Men Herschels papper beskrev lösningar för det ikosiska spelet endast på graferna för den vanliga tetraedern och den vanliga ikosaedern ; den beskrev inte Herschel-grafen. Namnet "the Herschel graph" gör ett tidigt framträdande i en grafteorilärobok av John Adrian Bondy och USR Murty , publicerad 1976. Men själva grafen beskrevs tidigare, till exempel av HSM Coxeter .



