Hamiltonsk nedbrytning

Waleckis Hamiltonska nedbrytning av hela grafen $K_{9}$

I grafteorin , en gren av matematiken, är en Hamiltonsk nedbrytning av en given graf en uppdelning av grafens kanter i Hamiltonska cykler . Hamiltons nedbrytningar har studerats både för oriktade grafer och för riktade grafer . I det oriktade fallet kan en Hamiltonsk nedbrytning också beskrivas som en 2-faktorisering av grafen så att varje faktor är sammankopplad.

Nödvändiga förutsättningar

För att en Hamiltons sönderdelning ska existera i en oriktad graf måste grafen vara sammankopplad och regelbunden av jämn grad . En riktad graf med en sådan sönderdelning måste vara starkt sammankopplad och alla hörn måste ha samma in-grad och ut-grad som varandra, men denna grad behöver inte vara jämn.

Särskilda klasser av grafer

Kompletta grafer

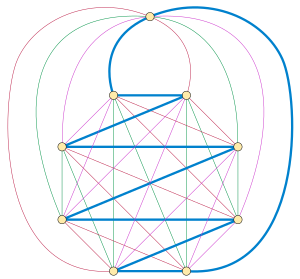
Varje komplett graf med ett udda nummer $n$ av hörn har en Hamiltonsk nedbrytning. Detta resultat, som är ett specialfall av Oberwolfach-problemet med att sönderdela kompletta grafer till isomorfa 2-faktorer, tillskrevs Walecki av Édouard Lucas 1892. Waleckis konstruktion placerar $n-1$ av hörnen till en regelbunden polygon och täcker hela grafen i denna delmängd av hörn med $(n-1)/2$ Hamiltonska banor som sicksackar tvärs över polygonen, med varje bana roterad från varandra med en multipel av $\pi /(n-1)$ . Banorna kan sedan alla slutföras till Hamiltons cykler genom att ansluta deras ändar genom den återstående vertexen.

Att expandera en vertex av en $2k$ -regelbunden graf till en klick av $2k$ hörn, en för varje ändpunkt av en kant vid den ersatta vertexen, kan inte ändra om grafen har en Hamiltonsk nedbrytning. Det omvända av denna expansionsprocess, genom att kollapsa en klick till en enda vertex, kommer att omvandla vilken Hamilton-nedbrytning som helst i den större grafen till en Hamilton-nedbrytning i den ursprungliga grafen. Omvänt kan Waleckis konstruktion appliceras på klicken för att expandera vilken Hamilton-nedbrytning som helst av den mindre grafen till en Hamilton-nedbrytning av den expanderade grafen.

En typ av analog till en komplett graf, i fallet med riktade grafer, är en turnering . Detta är en graf där varje par av distinkta hörn är förbundna med en enda riktad kant, från den ena till den andra; till exempel kan en sådan graf beskriva resultatet av en round-robin-turnering inom sport, där varje deltagare i turneringen spelar mot varandra, och kanterna riktas från förloraren i varje spel till vinnaren. Som svar på en gissning av Paul Kelly från 1968, bevisade Daniela Kühn och Deryk Osthus 2012 att varje tillräckligt stor vanlig turnering har en Hamiltonsk nedbrytning.

Plana grafer

Den mediala grafen för Herschel-grafen är en 4-regelbunden plan graf utan Hamiltons sönderdelning. De skuggade områdena motsvarar hörnen på den underliggande Herschel-grafen.

För 4-regelbundna plana grafer kan ytterligare nödvändiga villkor härledas från Grinbergs teorem . Ett exempel på en 4-regelbunden plan graf som inte uppfyller dessa villkor, och inte har en Hamiltonsk nedbrytning, ges av den mediala grafen för Herschel-grafen .

Prismor

Olöst problem i matematik :

Har varje prisma över en 3-kopplad 3-regelbunden graf en Hamiltonsk nedbrytning?

(fler olösta problem i matematik)

Prismat över en graf är dess kartesiska produkt med den kompletta grafen med två vertex. Till exempel är prismat över en cykelgraf grafen för ett geometriskt prisma . De 4-regelbundna graferna som erhållits som prismor över 3-regelbundna grafer har studerats särskilt med avseende på Hamiltons nedbrytning. När den underliggande 3-reguljära grafen är 3-vertex-ansluten , har det resulterande 4-reguljära prismat alltid en Hamiltonsk cykel och, i alla exempel som har testats, en Hamiltonsk sönderdelning. Baserat på denna observation antog Alspach och Rosenfeld 1986 att alla prismor över 3-regelbundna 3-vertex-anslutna grafer har en Hamiltonsk nedbrytning. Från och med 2015 förblir gissningen olöst.

Många klasser av 3-reguljära 3-vertex-kopplade grafer är kända för att ha prismor med Hamiltons sönderdelning. Detta inträffar särskilt när den 3-regelbundna grafen är plan och tvådelad, när den är en Halin-graf , när den i sig är ett prisma eller Möbius-stege , eller när det är en generaliserad Petersen-graf av ordning som är delbar med fyra.

Symmetriska grafer

Det finns oändligt många vertextransitiva grafer (grafer där varje vertex är symmetrisk med varannan vertex) som inte har en Hamiltonsk nedbrytning. I synnerhet gäller detta Cayley-graferna vars hörn beskriver elementen i en grupp och vars element beskriver multiplikation med generatorer av gruppen . Oändligt många 6-regelbundna Cayley-grafer har ingen Hamilton-nedbrytning, och det finns Cayley-grafer av godtyckligt stor jämn grad utan Hamilton-nedbrytning. Ett sätt att konstruera dessa grafer är att använda upprepade expansioner av klicker, som bevarar symmetri och inte kan ändra förekomsten av en Hamiltonsk nedbrytning.

Antal sönderdelningar

Varje 4-regelbunden oriktad graf har ett jämnt antal Hamiltonska nedbrytningar. Ännu starkare, för varannan kanter $e$ och $f$ av en 4-regelbunden graf, är antalet Hamiltonska uppdelningar där $e$ och $f$ tillhör samma cykel är jämn. Om en $2k$ -regelbunden graf har en Hamilton-nedbrytning, har den minst ett trippelt faktoriellt antal nedbrytningar,

$(3k-2)\cdot (3k-5)\cdots 7\cdot 4\cdot 1.$

Till exempel, 4-reguljära grafer som har en Hamiltonsk nedbrytning har minst fyra av dem; 6-regelbundna grafer som har en Hamilton-nedbrytning har minst 28, etc. Av detta följer att de enda graferna vars Hamilton-nedbrytningar är unika är cykelgraferna .

Beräkningskomplexitet

Att testa om en godtycklig graf har en Hamilton-nedbrytning är NP-komplett , både i riktade och oriktade fall. I synnerhet är frågan NP-komplett för vanliga grafer av en specificerad jämn grad; t.ex. för 4-regelbundna grafer.

Linjediagrammen för kubiska grafer är 4-regelbundna och har en Hamiltonsk nedbrytning om och endast om den underliggande kubiska grafen har en Hamiltonsk cykel. Som en konsekvens förblir Hamiltons sönderdelning NP-komplett för klasser av grafer som inkluderar linjediagram av hårda instanser av Hamiltons cykelproblem . Till exempel är Hamiltons sönderdelning NP-komplett för de 4-regelbundna plana graferna, eftersom de inkluderar linjegraferna för kubiska plana grafer. Å andra sidan innebär denna ekvivalens också att Hamiltons nedbrytning är lätt för 4-regelbundna linjediagram när deras underliggande kubiska grafer har lätta Hamiltonska cykelproblem.

Slumpmässiga reguljära grafer av jämn grad har nästan säkert en Hamiltonsk nedbrytning, och starkare finns det en randomiserad polynomisk tidsalgoritm som, när den ges som indata en slumpmässig vanlig graf av jämn grad, nästan säkert hittar en Hamiltonsk nedbrytning i den.

Se även

• Linjär arboricitet , en annan typ av begränsad uppdelning i subgrafer av maximal grad två