Funktionsval

Inom maskininlärning och statistik är funktionsval , även känt som variabelval , attributval eller urval av variabel delmängd , processen att välja en undergrupp av relevanta funktioner (variabler, prediktorer) för användning i modellkonstruktion. Funktionsvalstekniker används av flera skäl:

• förenkling av modeller för att göra dem lättare att tolka av forskare/användare,
• kortare träningstider,
• för att undvika dimensionalitetens förbannelse ,
• förbättra datakompatibiliteten med en inlärningsmodellklass,
• koda inneboende symmetrier som finns i inmatningsutrymmet.

Den centrala utgångspunkten när man använder en funktionsvalsteknik är att data innehåller vissa funktioner som antingen är redundanta eller irrelevanta , och kan därmed tas bort utan att förlora mycket information. Redundant och irrelevant är två distinkta begrepp, eftersom en relevant egenskap kan vara redundant i närvaro av en annan relevant egenskap med vilken den är starkt korrelerad.

Funktionsvalstekniker bör särskiljas från funktionsextraktion . Funktionsextraktion skapar nya funktioner från funktioner i de ursprungliga funktionerna, medan funktionsval returnerar en delmängd av funktionerna. Funktionsvalstekniker används ofta i domäner där det finns många funktioner och jämförelsevis få prov (eller datapunkter). Arketypiska fall för tillämpning av funktionsval inkluderar analys av skrivna texter och DNA-mikroarraydata , där det finns många tusentals funktioner, och några tiotals till hundratals prover.

Introduktion

En funktionsvalsalgoritm kan ses som en kombination av en sökteknik för att föreslå nya funktionsdelmängder, tillsammans med ett utvärderingsmått som ger poäng för de olika funktionsundermängderna. Den enklaste algoritmen är att testa varje möjlig delmängd av funktioner för att hitta den som minimerar felfrekvensen. Detta är en uttömmande sökning av utrymmet och är beräkningsmässigt svårhanterlig för alla utom de minsta funktionerna. Valet av utvärderingsmått påverkar kraftigt algoritmen, och det är dessa utvärderingsmått som skiljer mellan de tre huvudkategorierna av funktionsvalsalgoritmer: omslag, filter och inbäddade metoder.

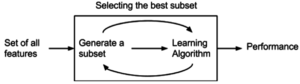
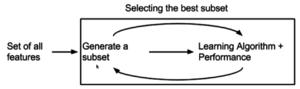
• Wrapper-metoder använder en prediktiv modell för att poängsätta funktionsdelmängder. Varje ny delmängd används för att träna en modell, som testas på ett uppehållsset. Att räkna antalet misstag som gjorts på den håll-out-uppsättningen (modellens felfrekvens) ger poängen för den delmängden. Eftersom inpackningsmetoder tränar en ny modell för varje delmängd är de mycket beräkningsintensiva, men ger vanligtvis den bästa funktionsuppsättningen för den specifika typen av modell eller typiska problem.
• Filtermetoder använder ett proxymått istället för felfrekvensen för att poängsätta en funktionsdelmängd. Detta mått är valt för att vara snabbt att beräkna, samtidigt som det fångar användbarheten av funktionsuppsättningen. Vanliga mått inkluderar den ömsesidiga informationen , den punktvisa ömsesidiga informationen , Pearson produkt-moment korrelationskoefficient , Relief-baserade algoritmer och inter/intra klass avstånd eller poängen för signifikanstest för varje klass/funktionskombination. Filter är vanligtvis mindre beräkningsintensiva än wrappers, men de producerar en funktionsuppsättning som inte är inställd på en specifik typ av prediktiv modell. Denna brist på inställning innebär att en funktionsuppsättning från ett filter är mer generell än uppsättningen från en wrapper, vilket vanligtvis ger lägre prediktionsprestanda än en wrapper. Funktionsuppsättningen innehåller dock inte antagandena om en förutsägelsemodell, och är därför mer användbar för att avslöja sambanden mellan funktionerna. Många filter tillhandahåller en funktionsrankning snarare än en explicit bästa funktionsdelmängd, och brytpunkten i rankningen väljs via korsvalidering . Filtermetoder har också använts som ett förbearbetningssteg för omslagsmetoder, vilket gör att ett omslag kan användas vid större problem. Ett annat populärt tillvägagångssätt är algoritmen Rekursiv Feature Elimination, som vanligtvis används med Support Vector Machines för att upprepade gånger konstruera en modell och ta bort funktioner med låg vikt.
• Inbäddade metoder är en samlad grupp av tekniker som utför funktionsval som en del av modellkonstruktionsprocessen. Exemplet på detta tillvägagångssätt är LASSO- metoden för att konstruera en linjär modell, som straffar regressionskoefficienterna med en L1-straff, vilket krymper många av dem till noll. Alla funktioner som har regressionskoefficienter som inte är noll är "valda" av LASSO-algoritmen. Förbättringar av LASSO inkluderar Bolasso som fixerar prover; Elastisk nettoreglering , som kombinerar L1-straffet för LASSO med L2-straffet för åsregression ; och FeaLect som poängsätter alla funktioner baserat på kombinatorisk analys av regressionskoefficienter. AEFS utökar LASSO ytterligare till icke-linjära scenarier med autoencoders. Dessa tillvägagångssätt tenderar att ligga mellan filter och omslag när det gäller beräkningskomplexitet.

I traditionell regressionsanalys är den mest populära formen av funktionsval stegvis regression , vilket är en inpackningsteknik. Det är en girig algoritm som lägger till den bästa funktionen (eller tar bort den sämsta funktionen) vid varje omgång. Den huvudsakliga kontrollfrågan är att bestämma när algoritmen ska stoppas. I maskininlärning görs detta vanligtvis genom korsvalidering . I statistiken är vissa kriterier optimerade. Detta leder till det inneboende problemet med häckning. Mer robusta metoder har utforskats, såsom gren- och bundna och bitvis linjära nätverk.

Val av delmängd

Val av delmängd utvärderar en delmängd av funktioner som en grupp för lämplighet. Algoritmer för urval av delmängder kan delas upp i omslag, filter och inbäddade metoder. Wrappers använder en sökalgoritm för att söka igenom utrymmet med möjliga funktioner och utvärdera varje delmängd genom att köra en modell på delmängden. Omslag kan vara beräkningsmässigt dyra och har en risk för överpassning till modellen. Filter liknar wrappers i sökmetoden, men istället för att utvärdera mot en modell utvärderas ett enklare filter. Inbäddade tekniker är inbäddade i, och specifika för, en modell.

Många populära sökmetoder använder girig backklättring , som iterativt utvärderar en kandidatundergrupp av funktioner, sedan modifierar delmängden och utvärderar om den nya delmängden är en förbättring jämfört med den gamla. Utvärdering av delmängderna kräver ett poängmått som betygsätter en delmängd av funktioner. En uttömmande sökning är i allmänhet opraktisk, så vid någon av implementeraren (eller operatören) definierad stopppunkt, väljs den delmängd av funktioner med den högsta poängen som upptäckts fram till den punkten som den tillfredsställande egenskapsdelmängden. Stoppkriteriet varierar beroende på algoritm; möjliga kriterier inkluderar: en delmängds poäng överstiger en tröskel, ett programs maximalt tillåtna körtid har överskridits, etc.

Alternativa sökbaserade tekniker är baserade på riktad projektionssträvan som hittar lågdimensionella projektioner av data som ger högt betyg: de egenskaper som har de största projektionerna i det lägre dimensionella rummet väljs sedan ut.

Sökmetoder inkluderar:

• Uttömmande
• Bästa först
• Simulerad glödgning
• Genetisk algoritm
• Girigt framåt urval
• Girig bakåteliminering
• Partikelsvärmoptimering
• Riktad projektionssträvan
• Spridningssökning
• Variabel grannsökning

Två populära filtermått för klassificeringsproblem är korrelation och ömsesidig information , även om det inte heller är sanna mått eller "avståndsmått" i matematisk mening, eftersom de inte följer triangelojämlikheten och därför inte beräknar någon faktisk "avstånd" - de borde snarare betraktas som "poäng". Dessa poäng beräknas mellan en kandidatfunktion (eller en uppsättning funktioner) och den önskade utdatakategorin. Det finns dock sanna mått som är en enkel funktion av den ömsesidiga informationen; se här .

Andra tillgängliga filtermått inkluderar:

• Klassskiljbarhet
  • Sannolikhet för fel
  • Interklassdistans
  • Probabilistiskt avstånd
  • Entropi
• Konsistensbaserat funktionsval
• Korrelationsbaserat funktionsval

Optimalitetskriterier

Valet av optimalitetskriterier är svårt eftersom det finns flera mål i en funktionsvalsuppgift. Många vanliga kriterier inkluderar ett mått av noggrannhet, bestraffad av antalet valda funktioner. Exempel inkluderar Akaike informationskriterium (AIC) och Mallows's C _p , som har en straffavgift på 2 för varje tillagd funktion. AIC är baserad på informationsteori och härleds effektivt via principen om maximal entropi .

Andra kriterier är Bayesianskt informationskriterium (BIC), som använder ett straff av ${\sqrt {\log {n}}}$ för varje tillagd funktion, minsta beskrivningslängd (MDL) som asymptotiskt använder ${\sqrt {\log {n}}}$ , Bonferroni / RIC som använder ${\sqrt {2\log {p}}}$ , urval av maximalt beroendefunktion och en mängd olika av nya kriterier som är motiverade av falsk upptäcktsfrekvens (FDR), som använder något nära ${\sqrt {2\log {\frac {p}{q}}}}$ . Ett kriterium för maximal entropihastighet kan också användas för att välja den mest relevanta underuppsättningen av funktioner.

Strukturera lärande

Val av filterfunktioner är ett specifikt fall av ett mer allmänt paradigm som kallas strukturinlärning . Funktionsval hittar den relevanta funktionsuppsättningen för en specifik målvariabel medan strukturinlärning hittar sambanden mellan alla variabler, vanligtvis genom att uttrycka dessa samband som en graf. De vanligaste strukturinlärningsalgoritmerna antar att data genereras av ett Bayesian Network , och därför är strukturen en riktad grafisk modell . Den optimala lösningen på problemet med val av filterfunktion är målnodens Markov-filt , och i ett Bayesian-nätverk finns det en unik Markov-filt för varje nod.

Informationsteoribaserade funktionsvalsmekanismer

Det finns olika funktionsvalsmekanismer som använder ömsesidig information för att poängsätta de olika funktionerna. De använder vanligtvis samma algoritm:

1. Beräkna den ömsesidiga informationen som poäng för mellan alla funktioner ( $f_{i}\in F$ ) och målklassen ( c )
2. Välj funktionen med störst poäng (t.ex. ${\underset {f_{i}\in F}{\operatörsnamn {argmax} }}(I(f_ {i},c))$ ) och lägg till den i uppsättningen av valda funktioner ( S )
3. Beräkna poängen som kan härledas från den ömsesidiga informationen
4. Välj objektet med högst poäng och lägg till det i uppsättningen av utvalda funktioner (t.ex. ${\underset {f_{i} \in F}{\operatörsnamn {argmax} }}(I_{derived}(f_{i},c))$ )
5. Upprepa 3. och 4. tills ett visst antal funktioner har valts (t.ex. $|S|=l$ )

Den enklaste metoden använder den ömsesidiga informationen som den "härledda" poängen.

Det finns dock olika tillvägagångssätt som försöker minska redundansen mellan funktioner.

Val av funktioner för minimum-redundans-maximum-relevans (mRMR).

Peng et al. föreslagit en funktionsvalmetod som kan använda antingen ömsesidig information, korrelation eller distans/likhetspoäng för att välja egenskaper. Syftet är att straffa en funktions relevans genom dess redundans i närvaro av de andra valda funktionerna. Relevansen av en egenskapsuppsättning S fi _för klassen c definieras av medelvärdet av alla ömsesidiga informationsvärden mellan den individuella egenskapen och klassen c enligt följande:

$D(S,c)={\frac {1}{|S|}}\summa _{f_{i}\in S}I(f_{ i};c)$ .

fi _särdrag i uppsättningen S är medelvärdet av alla ömsesidiga informationsvärden mellan särdraget och särdraget f _j :

$R(S)={\frac {1}{|S|^{2}}}\summa _{f_{i}, f_{j}\in S}I(f_{i};f_{j})$

mRMR-kriteriet är en kombination av två mått som anges ovan och definieras enligt följande:

$\mathrm {mRMR} =\max _{S}\left[{\frac {1}{|S|}}\summa _{f_{i}\in S}I(f_{i};c )-{\frac {1}{|S|^{2}}}\summa _{f_{i},f_{j}\in S}I(f_{i};f_{j})\right] .$

indicator function Anta att det finns n kompletta funktioner. Låt x _i vara uppsättningsmedlemskapsindikatorfunktionen för egenskap _fi , så att xi ₌ 1 indikerar närvaro och xi ₌ =0 indicates absence of the feature f_i in the globally optimal feature set. Let $c_{i}=I(f_{i};c)$ and $a_{ij}=I(f_{i};f_{j})$. The above may then be written as an optimization problem:

$\mathrm {mRMR} =\max _{x\in \{0,1\}^{n}}\left[{\frac {\sum _{i=1}^{n}c_{i }x_{i}}{\sum _{i=1}^{n}x_{i}}}-{\frac {\sum _{i,j=1}^{n}a_{ij}x_{ i}x_{j}}{(\summa _{i=1}^{n}x_{i})^{2}}}\höger].$

mRMR-algoritmen är en approximation av den teoretiskt optimala funktionsvalalgoritmen för maximalt beroende som maximerar den ömsesidiga informationen mellan den gemensamma fördelningen av de valda funktionerna och klassificeringsvariabeln. Eftersom mRMR approximerar det kombinatoriska uppskattningsproblemet med en serie mycket mindre problem, som vart och ett endast involverar två variabler, använder den alltså parvisa gemensamma sannolikheter som är mer robusta. I vissa situationer kan algoritmen underskatta användbarheten av funktioner eftersom den inte har något sätt att mäta interaktioner mellan funktioner som kan öka relevansen. Detta kan leda till dålig prestanda när funktionerna individuellt är oanvändbara, men är användbara när de kombineras (ett patologiskt fall hittas när klassen är en paritetsfunktion av funktionerna). Generellt sett är algoritmen mer effektiv (i termer av mängden data som krävs) än det teoretiskt optimala maxberoendevalet, men producerar ändå en funktionsuppsättning med liten parvis redundans.

mRMR är ett exempel på en stor klass av filtermetoder som på olika sätt avväger mellan relevans och redundans.

Val av kvadratisk programmeringsfunktion

mRMR är ett typiskt exempel på en inkrementell girig strategi för funktionsval: när en funktion väl har valts kan den inte väljas bort i ett senare skede. Även om mRMR skulle kunna optimeras med hjälp av flytande sökning för att minska vissa funktioner, kan det också omformuleras som ett globalt kvadratiskt programmeringsoptimeringsproblem enligt följande:

$\mathrm {QPFS} :\min _{\mathbf {x} }\left\{\alpha \mathbf {x} ^{T}H\mathbf {x} -\mathbf {x} ^{T}F\right\}\quad {\mbox{st}}\ \sum _ {i=1}^{n}x_{i}=1,x_{i}\geq 0$

där $F_{n\times 1}=[I(f_{1};c),\ldots ,I(f_{n};c)]^{T}$ är vektorn för egenskapens relevans förutsatt att det finns n egenskaper totalt, ${\displaystyle H_{n\times n}=[I(f_{i};f_{j})]_{i,j=1\ldots n}} är matrisen för funktion parvis redundans,$ och $\mathbf {x} _{n\ gånger 1}$ representerar relativa objektvikter. QPFS löses via kvadratisk programmering. Det har nyligen visat sig att QFPS är partisk mot funktioner med mindre entropi, på grund av dess placering av egenskapens självredundansterm $I(f_{i};f_{i})$ på diagonal av H .

Villkorlig ömsesidig information

En annan poäng som erhålls för den ömsesidiga informationen är baserad på den villkorade relevansen:

$\mathrm {SPEC_{CMI}} :\max _{\mathbf {x} }\left \{\mathbf {x} ^{T}Q\mathbf {x} \right\}\quad {\mbox{st}}\ \|\mathbf {x} \|=1,x_{i}\geq 0$

där ${\displaystyle Q_{ii}=I(f_{i};c)$${ \displaystyle Q_{ij}=I(f_{i};c|f_{j}),i\neq j}$ och .

En fördel med SPEC _CMI är att det enkelt kan lösas genom att hitta den dominanta egenvektorn för Q , vilket är mycket skalbart. SPEC _CMI hanterar också interaktion med andra ordningens funktioner.

Gemensam ömsesidig information

I en studie av olika poäng har Brown et al. rekommenderade den gemensamma ömsesidiga informationen som ett bra betyg för funktionsval. Poängen försöker hitta den funktion som lägger till mest ny information till de redan valda funktionerna, för att undvika redundans. Poängen är formulerad enligt följande:

${\begin{aligned}JMI(f_{i})&=\sum _{ f_{j}\in S}(I(f_{i};c)+I(f_{i};c|f_{j}))\\&=\summa _{f_{j}\in S} {\bigl [}I(f_{j};c)+I(f_{i};c)-{\bigl (}I(f_{i};f_{j})-I(f_{i}; f_{j}|c){\bigr )}{\bigr ]}\end{aligned}}$

Poängen använder den villkorade ömsesidiga informationen och den ömsesidiga informationen för att uppskatta redundansen mellan de redan valda funktionerna ( ${\displaystyle f_{j}\in S} )$ och funktionen som undersöks ( $f_{ i}$ ).

Hilbert-Schmidt Independence Criterion Lassobaserad funktionsval

För högdimensionella och små provdata (t.ex. dimensionalitet > 10 ⁵ och antalet prov < 10 ³ ), är Hilbert-Schmidts oberoende kriterium Lasso (HSIC Lasso) användbar. HSIC Lasso optimeringsproblem ges som

$\mathrm {HSIC_{Lasso}} :\min _{\mathbf {x} }{\frac {1}{2}}\summa _ {k,l=1}^{n}x_{k}x_{l}{\mbox{HSIC}}(f_{k},f_{l})-\summa _{k=1}^{n} x_{k}{\mbox{HSIC}}(f_{k},c)+\lambda \|\mathbf {x} \|_{1},\quad {\mbox{st}}\ x_{1} ,\ldots ,x_{n}\geq 0,$

där ${\displaystyle {\mbox{HSIC}}(f_{k},c)={\mbox{tr}}({\bar { \mathbf {K} }}^{(k)}{\bar {\mathbf {L} }})} är$ ett kärnbaserat oberoendemått som kallas det (empiriska) Hilbert-Schmidt oberoende kriteriet (HSIC), ${\mbox{tr}}(\cdot )$ anger spåret , $\lambda$ är regulariseringsparametern, ${\displaystyle {\bar {\mathbf {K} }}^{(k)}=\mathbf {\Gamma } \mathbf {K} ^{(k)}\mathbf {\Gamma } } och L ¯$ = ${ \bar {\mathbf {L} }}=\mathbf {\Gamma } \mathbf {L} \mathbf {\Gamma } } är$ in- och utgångscentrerade grammatriser , ${\displaystyle K_{i,j}^{(k)}=K(u_{k,i},u_{k,j})$$L_{i,j}=L(c_{i},c_{j})$ och är grammatriser, $K(u,u')$ och $L(c,c')$ är kärnfunktioner, ${\displaystyle \mathbf {\Gamma } =\mathbf {I} _ {m}-{\frac {1}{m}}\mathbf {1} _{m}\mathbf {1} _{m}^{T}} är centreringsmatrisen, I m {\$ displaystyle ${ I} _{m}}$ är den m -dimensionella identitetsmatrisen ( m : antalet sampel), $\mathbf {1} _{m}$ är den m -dimensionella vektorn med alla ettor, och $\|\cdot \|_{1}$ är $\ell _{1}$ -normen. HSIC tar alltid ett icke-negativt värde och är noll om och endast om två slumpvariabler är statistiskt oberoende när en universell reproducerande kärna som den Gaussiska kärnan används.

HSIC Lasso kan skrivas som

$\mathrm {HSIC_{Lasso}} :\min _{\mathbf {x} }{\frac {1}{2}}\left\|{\bar {\mathbf {L} }}-\summa _{k=1}^{n}x_{k}{\bar {\mathbf {K}}}^{(k)}\right\|_{F}^{2}+\lambda \|\mathbf {x} \|_{1},\quad {\mbox{st}}\ x_{1},\ldots ,x_{n}\geq 0,$

där $\|\cdot \|_{F}$ är Frobenius-normen . Optimeringsproblemet är ett lassoproblem, och därför kan det lösas effektivt med en toppmodern lassolösare som den dubbla förstärkta Lagrangian-metoden .

Val av korrelationsfunktion

Korrelationsfunktionsurvalsmåttet (CFS) utvärderar delmängder av särdrag på basis av följande hypotes: "Bra särdragsundermängder innehåller särdrag som är starkt korrelerade med klassificeringen, men ändå okorrelerade till varandra". Följande ekvation ger fördelarna med en delmängd S som består av k egenskaper:

$\mathrm {Merit} _{S_{k}}={\frac {k{\overline {r_{cf}}}}{\sqrt {k+k(k-1){\overline {r_{ ff}}}}}}.$

Här är ${\overline {r_{cf}}}$ medelvärdet för alla funktionsklassificeringskorrelationer, och ${\overline {r_{ff}}}$ är det genomsnittliga värdet av alla funktion-funktion korrelationer. CFS-kriteriet definieras enligt följande:

$\mathrm {CFS} =\max _{S_{k}}\left[{\frac {r_{cf_{1}}+r_{cf_{2}}+\cdots +r_{cf_{k} }}{\sqrt {k+2(r_{f_{1}f_{2}}+\cdots +r_{f_{i}f_{j}}+\cdots +r_{f_{k}f_{k- 1}})}}}\höger].$

Variablerna $r_{cf_{i}}$ och $r_{f_{i}f_{j}}$ hänvisas till som korrelationer, men är inte nödvändigtvis Pearsons korrelation koefficient eller Spearmans ρ . Halls avhandling använder ingen av dessa, utan använder tre olika mått på släktskap, minsta beskrivningslängd (MDL), symmetrisk osäkerhet och lättnad .

Låt x _i vara den inställda medlemskapsindikatorfunktionen för funktion f _i ; då kan ovanstående skrivas om som ett optimeringsproblem:

$\mathrm {CFS} =\max _{x\in \{0,1\}^{n}}\left[{\frac {(\sum _{i=1}^{n}a_{ i}x_{i})^{2}}{\sum _{i=1}^{n}x_{i}+\sum _{i\neq j}2b_{ij}x_{i}x_{j }}}\höger].$

De kombinatoriska problemen ovan är i själva verket blandade 0–1 linjära programmeringsproblem som kan lösas genom att använda branch-and-bound algoritmer .

Regelbundna träd

Funktionerna från ett beslutsträd eller en trädensemble visas vara överflödiga. En ny metod som kallas regularized tree kan användas för val av funktionsdelmängder. Regulariserade träd straffar med en variabel som liknar de variabler som valts vid tidigare trädnoder för att dela upp den aktuella noden. Regulariserade träd behöver bara bygga en trädmodell (eller en trädensemblemodell) och är därför beräkningseffektiva.

Regulariserade träd hanterar naturligt numeriska och kategoriska egenskaper, interaktioner och olinjäriteter. De är oföränderliga för att tillskriva skalor (enheter) och okänsliga för extremvärden , och kräver därför lite förbearbetning av data såsom normalisering . Regularized Random Forest (RRF) är en typ av regulariserade träd. Den guidade RRF är en förstärkt RRF som styrs av viktpoängen från en vanlig slumpmässig skog.

Översikt över metaheuristiska metoder

En metaheuristik är en allmän beskrivning av en algoritm dedikerad för att lösa svåra (typiskt NP-hårda problem) optimeringsproblem för vilka det inte finns några klassiska lösningsmetoder. I allmänhet är en metaheuristik en stokastisk algoritm som tenderar att nå ett globalt optimum. Det finns många metaheuristiker, från en enkel lokal sökning till en komplex global sökalgoritm.

Huvudprinciper

Funktionsvalsmetoderna presenteras vanligtvis i tre klasser baserat på hur de kombinerar urvalsalgoritmen och modellbyggnaden.

Filtermetod

Filtermetod för val av funktion

Filtertypmetoder väljer variabler oavsett modell. De baseras endast på allmänna egenskaper som korrelationen med variabeln som ska förutsägas. Filtermetoder undertrycker de minst intressanta variablerna. De andra variablerna kommer att ingå i en klassificering eller en regressionsmodell som används för att klassificera eller förutsäga data. Dessa metoder är särskilt effektiva när det gäller beräkningstid och robusta mot överanpassning.

Filtermetoder tenderar att välja redundanta variabler när de inte tar hänsyn till sambanden mellan variabler. Men mer utarbetade funktioner försöker minimera detta problem genom att ta bort variabler som är starkt korrelerade till varandra, som algoritmen Fast Correlation Based Filter (FCBF).

Inpackningsmetod

Omslagsmetod för val av funktion

Wrapper-metoder utvärderar delmängder av variabler som, till skillnad från filtermetoder, tillåter att detektera möjliga interaktioner mellan variabler. De två huvudsakliga nackdelarna med dessa metoder är:

• Den ökande överanpassningsrisken när antalet observationer är otillräckligt.
• Den signifikanta beräkningstiden när antalet variabler är stort.

Inbäddad metod

Inbäddad metod för val av funktioner

Inbäddade metoder har nyligen föreslagits som försöker kombinera fördelarna med båda tidigare metoderna. En inlärningsalgoritm drar fördel av sin egen variabelvalsprocess och utför funktionsval och klassificering samtidigt, såsom FRMT-algoritmen.

Tillämpning av metaheuristik för funktionsval

Detta är en undersökning av tillämpningen av funktionsvalsmetaheuristik som nyligen använts i litteraturen. Denna undersökning genomfördes av J. Hammon i sin avhandling från 2013.

Ansökan	Algoritm	Närma sig	Klassificerare	Utvärderingsfunktion	Referens
SNP	Funktionsval med hjälp av Feature Similarity	Filtrera		r 2	Phuong 2005
SNP	Genetisk algoritm	Omslag	Beslutsträd	Klassificeringsnoggrannhet (10 gånger)	Shah 2004
SNP	bergsklättring	Filter + omslag	Naiv Bayesian	Förutspådd restsumma av kvadrater	Långt 2007
SNP	Simulerad glödgning		Naiv bayesian	Klassificeringsnoggrannhet (5-faldig)	Ustunkar 2011
Segment villkorlig frigivning	Myrkoloni	Omslag	Artificiellt neuralt nätverk	MSE	Al-ani 2005
Marknadsföring	Simulerad glödgning	Omslag	Regression	AIC , r 2	Meiri 2006
Ekonomi	Simulerad glödgning, genetisk algoritm	Omslag	Regression	BIC	Kapetanios 2007
Spektral massa	Genetisk algoritm	Omslag	Multipel linjär regression, partiella minsta kvadrater	root-mean-square fel av förutsägelse	Broadhurst et al. 1997
Spam	Binär PSO + mutation	Omslag	Beslutsträd	vägd kostnad	Zhang 2014
Microarray	Tabu-sökning + PSO	Omslag	Support Vector Machine , K Närmaste grannar	Euklidiskt avstånd	Chuang 2009
Microarray	PSO + Genetisk algoritm	Omslag	Stöd Vector Machine	Klassificeringsnoggrannhet (10 gånger)	Alba 2007
Microarray	Genetisk algoritm + Itererad lokal sökning	Inbäddad	Stöd Vector Machine	Klassificeringsnoggrannhet (10 gånger)	Duval 2009
Microarray	Itererad lokal sökning	Omslag	Regression	Posterior sannolikhet	Hans 2007
Microarray	Genetisk algoritm	Omslag	K Närmaste grannar	Klassificeringsnoggrannhet ( korsvalidering utelämna en utestående )	Jirapech-Umpai 2005
Microarray	Hybrid genetisk algoritm	Omslag	K Närmaste grannar	Klassificeringsnoggrannhet (korsvalidering utelämna en ut)	Åh 2004
Microarray	Genetisk algoritm	Omslag	Stöd Vector Machine	Känslighet och specificitet	Xuan 2011
Microarray	Genetisk algoritm	Omslag	Alla parade Support Vector Machine	Klassificeringsnoggrannhet (korsvalidering utelämna en ut)	Peng 2003
Microarray	Genetisk algoritm	Inbäddad	Stöd Vector Machine	Klassificeringsnoggrannhet (10 gånger)	Hernandez 2007
Microarray	Genetisk algoritm	Hybrid	Stöd Vector Machine	Klassificeringsnoggrannhet (korsvalidering utelämna en ut)	Huerta 2006
Microarray	Genetisk algoritm		Stöd Vector Machine	Klassificeringsnoggrannhet (10 gånger)	Muni 2006
Microarray	Genetisk algoritm	Omslag	Stöd Vector Machine	EH-DIALL, KLUMP	Jourdan 2005
Alzheimers sjukdom	Welchs t-test	Filtrera	Stöd vektor maskin	Klassificeringsnoggrannhet (10 gånger)	Zhang 2015
Datorsyn	Oändligt urval av funktioner	Filtrera	Oberoende	Genomsnittlig precision , ROC AUC	Roffo 2015
Mikroarrayer	Egenvektorcentralitet FS	Filtrera	Oberoende	Genomsnittlig precision, noggrannhet, ROC AUC	Roffo & Melzi 2016
XML	Symmetrisk Tau (ST)	Filtrera	Strukturell associativ klassificering	Noggrannhet, täckning	Shaharanee & Hadzic 2014

Funktionsval inbäddat i inlärningsalgoritmer

Vissa inlärningsalgoritmer utför funktionsval som en del av sin övergripande operation. Dessa inkluderar:

• $l_{1}$ -regulariseringstekniker, såsom sparse regression, LASSO och $l_{1}$ -SVM
• Regulariserade träd, t.ex. regularized random skog implementerad i RRF-paketet
• Beslutsträd
• Memetisk algoritm
• Random multinomial logit (RMNL)
• Automatisk kodning av nätverk med ett flaskhalslager
• Submodulärt funktionsval
• Lokalt inlärningsbaserat funktionsval. Jämfört med traditionella metoder innebär det ingen heuristisk sökning, kan enkelt hantera problem med flera klasser och fungerar för både linjära och icke-linjära problem. Det stöds också av en stark teoretisk grund. Numeriska experiment visade att metoden kan uppnå en nära optimal lösning även när data innehåller >1M irrelevanta egenskaper.
• Rekommendationssystem baserat på funktionsval. Funktionsvalsmetoderna introduceras i rekommendatorsystemforskning.

Se även

• Klusteranalys
• Data mining
• Dimensionalitetsreduktion
• Särdragsextraktion
• Hyperparameteroptimering
• Modellval
• Relief (funktionsval)

Vidare läsning

• Guyon, Isabelle; Elisseeff, Andre (2003). "En introduktion till variabel- och funktionsval" . Journal of Machine Learning Research . 3 : 1157-1182.
•   Harrell, F. (2001). Regressionsmodelleringsstrategier . Springer. ISBN 0-387-95232-2 .
•   Liu, Huan; Motoda, Hiroshi (1998). Funktionsval för Knowledge Discovery och Data Mining . Springer. ISBN 0-7923-8198-X .
•   Liu, Huan; Yu, Lei (2005). "Mot att integrera funktionsvalsalgoritmer för klassificering och klustring". IEEE-transaktioner på kunskaps- och datateknik . 17 (4): 491–502. doi : 10.1109/TKDE.2005.66 . S2CID 1607600 .

externa länkar

• Funktionsvalspaket, Arizona State University (Matlab-kod)
• NIPS challenge 2003 (se även NIPS )
• Naiv Bayes-implementering med funktionsval i Visual Basic (inkluderar körbar och källkod)
• Program för val av funktioner för minimum-redundans-maximum-relevans (mRMR).
• FEAST (Öppen källkod för funktionsvalsalgoritmer i C och MATLAB)