Ömsesidig information

Venndiagram som visar additiva och subtraktiva samband mellan olika informationsmått associerade med korrelerade variabler $X$ och $Y$ . Arean som endera cirklarna innehåller är den gemensamma entropin $\mathrm {H} (X,Y)$ . Cirkeln till vänster (röd och violett) är den individuella entropin ${\displaystyle \mathrm {H} (X)} ,$ där den röda är den villkorliga entropin $\mathrm { H} (X\mitt Y)$ . Cirkeln till höger (blå och violett) är $\mathrm {H} (Y)$ , där den blå är $\mathrm {H} (Y\mid X)$ . Den violetta är den ömsesidiga informationen $\operatorname {I} (X;Y)$ .

Inom sannolikhetsteori och informationsteori är den ömsesidiga informationen ( MI ) för två slumpvariabler ett mått på det ömsesidiga beroendet mellan de två variablerna. Mer specifikt kvantifierar den " mängden information " (i enheter som shannoner ( bitar ), nats eller hartleys ) som erhålls om en slumpvariabel genom att observera den andra slumpvariabeln. Begreppet ömsesidig information är intimt kopplat till entropi av en slumpvariabel, en grundläggande föreställning inom informationsteorin som kvantifierar den förväntade "mängden information" som hålls i en slumpvariabel.

Inte begränsat till verkligt värderade slumpvariabler och linjärt beroende som korrelationskoefficienten , MI är mer generell och bestämmer hur olika den gemensamma fördelningen av paret $(X,Y)$ är från produkten av marginalfördelningar av $X$ och $Y$ . MI är det förväntade värdet av den punktvisa ömsesidiga informationen (PMI).

Kvantiteten definierades och analyserades av Claude Shannon i hans landmärke " A Mathematical Theory of Communication ", även om han inte kallade det "ömsesidig information". Denna term myntades senare av Robert Fano . Ömsesidig information är också känd som informationsvinst .

Definition

Låt $(X,Y)$ vara ett par slumpvariabler med värden över mellanrummet ${\mathcal {X}}\times {\mathcal {Y}}$ . Om deras gemensamma fördelning är $P_{(X,Y)}$ och marginalfördelningarna är $P_{X}$ och $P_{Y}$ , den ömsesidiga informationen definieras som

$I(X;Y)=D_{\mathrm {KL} }(P_{(X,Y) }\|P_{X}\ibland P_{Y})$

där $D_{\mathrm {KL} }$ är Kullback–Leibler-divergensen .

Lägg märke till, enligt egenskapen för Kullback–Leibler-divergensen , att $I(X;Y)$ är lika med noll precis när den gemensamma fördelningen sammanfaller med produkten av marginalerna, dvs när ${ \displaystyle X}$ och $Y$ är oberoende (och följaktligen säger ${\displaystyle Y} ingenting om$$X$ ). $I(X;Y)$ är icke-negativ, det är ett mått på priset för kodning $(X,Y)$ som ett par oberoende slumpmässiga variabler när de i verkligheten inte är det.

Om den naturliga logaritmen används är enheten för ömsesidig information nat . Om logbasen 2 används är enheten för ömsesidig information shannon , även känd som biten. Om logbasen 10 används är enheten för ömsesidig information hartley , även känd som ban eller dit.

När det gäller PMF för diskreta distributioner

Den ömsesidiga informationen för två gemensamt diskreta slumpvariabler $X$ och $Y$ beräknas som en dubbelsumma:

$\operatorname {I} (X;Y)=\summa _{y\in {\mathcal {Y}}}\summa _{x\in {\mathcal {X}}}{P_{ (X,Y)}(x,y)\log \left({\frac {P_{(X,Y)}(x,y)}{P_{X}(x)\,P_{Y}(y )}}\höger)},$

 

 

 

 

()

där $P_{(X,Y)}$ är den gemensamma sannolikhetsmassfunktionen för \ X $\displaystyle X}$ och $displaystyle Y}$ och $P_{X}$ och $P_{Y}$ är de marginella sannolikhetsmassfunktionerna för $X$ respektive $Y$ .

När det gäller PDF-filer för kontinuerliga distributioner

I fallet med gemensamt kontinuerliga stokastiska variabler ersätts dubbelsumman med en dubbelintegral :

$\operatorname {I} (X;Y)=\int _{\mathcal {Y}}\int _{\mathcal {X}}{P_{(X,Y)}(x,y )\log {\left({\frac {P_{(X,Y)}(x,y)}{P_{X}(x)\,P_{Y}(y)}}\höger)}}\ ;dx\,dy,$

 

 

 

 

()

där $P_{(X,Y)}$ är nu den gemensamma sannolikhetstäthetsfunktionen för X $\displaystyle X}$ och $Y$ och $P_{X }$ och $P_{Y}$ är de marginella sannolikhetstäthetsfunktionerna för $X$ respektive $Y$ .

Motivering

Intuitivt mäter ömsesidig information informationen som $X$ och $Y$ delar: Den mäter hur mycket kunskap om en av dessa variabler minskar osäkerheten om den andra. Till exempel, om $X$ och $Y$ är oberoende, så ger att veta $X$ ingen information om $Y$ och vice versa, så deras ömsesidiga information är noll . I den andra ytterligheten, om $X$ är en deterministisk funktion av $Y$ och $Y$ är en deterministisk funktion av $X$ då all information som förmedlas av $X$ delas med $Y$ : att veta $X$ bestämmer värdet på $Y$ och vice versa. Som ett resultat är den ömsesidiga informationen i detta fall densamma som osäkerheten i $Y$ (eller $X$ ), nämligen entropin för $Y$ (eller ${\ displaystil X}$ ). Dessutom är denna ömsesidiga information densamma som entropin för $X$ och som entropin för $Y$ . (Ett mycket speciellt fall av detta är när $X$ och $Y$ är samma slumpvariabel.)

Ömsesidig information är ett mått på det inneboende beroendet uttryckt i den gemensamma fördelningen av $X$ och $Y$ i förhållande till marginalfördelningen av $X$ och $Y$ under antagandet av självständighet. Ömsesidig information mäter därför beroende i följande mening: $\operatorname {I} (X;Y)=0$ om och endast om $X$ och $Y$ är oberoende slumpvariabler. Detta är lätt att se i en riktning: om $X$ och $Y$ är oberoende, då ${\displaystyle p_{(X,Y)}(x,y)=p_{X}(x)\cdot p_{Y}(y)} , och därför$ :

$\log {\left({\frac {p_{(X, Y)}(x,y)}{p_{X}(x)\,p_{Y}(y)}}\right)}=\log 1=0.$

Dessutom är ömsesidig information icke-negativ (dvs. $\operatorname {I} (X;Y)\geq 0$ se nedan) och symmetrisk (dvs. $\operatörsnamn {I} (X;Y)=\operatörsnamn {I} (Y;X)$ se nedan).

Egenskaper

Icke-negativitet

Med hjälp av Jensens ojämlikhet på definitionen av ömsesidig information kan vi visa att $\operatorname {I} (X;Y)$ är icke-negativ, dvs.

$\operatörsnamn {I} (X;Y)\geq 0$

Symmetri

$\operatörsnamn {I} (X;Y)=\operatörsnamn {I} (Y;X)$

Beviset ges med tanke på sambandet med entropi, som visas nedan.

Relation till betingad och ledentropi

Ömsesidig information kan uttryckas på samma sätt som:

${\begin{aligned}\operatörsnamn {I} (X;Y)&{}\equiv \mathrm {H} (X )-\mathrm {H} (X\mid Y)\\&{}\equiv \mathrm {H} (Y)-\mathrm {H} (Y\mid X)\\&{}\equiv \mathrm { H} (X)+\mathrm {H} (Y)-\mathrm {H} (X,Y)\\&{}\ekvivalent \mathrm {H} (X,Y)-\mathrm {H} (X \mid Y)-\mathrm {H} (Y\mid X)\end{aligned}}$

där $\mathrm {H} (X)$ och $displaystyle \mathrm {H} (Y)}$ \ är marginalentropierna , $\mathrm {H} (X\mid Y)$ och $\mathrm {H} (Y\mid X)$ är de villkorliga entropierna och $\mathrm { H} (X,Y)$ är den gemensamma entropin för $X$ och $Y$ .

Lägg märke till analogin till föreningen, skillnaden och skärningspunkten mellan två uppsättningar: i detta avseende framgår alla formlerna ovan från Venn-diagrammet som rapporterades i början av artikeln.

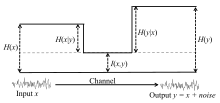
När det gäller en kommunikationskanal där utgången $Y$ är en brusig version av ingången $X$ , är dessa relationer sammanfattade i figuren:

Sambanden mellan informationsteoretiska storheter

Eftersom $\operatorname {I} (X;Y)$ är icke-negativ, följaktligen $\mathrm {H} (X )\geq \mathrm {H} (X\mitt Y)$ . Här ger vi den detaljerade deduktionen av $\operatornamn {I} (X;Y)=\mathrm {H} (Y)-\ mathrm {H} (Y\mid X)$ för fallet med gemensamt diskreta slumpvariabler:

${\begin{aligned}\operatörsnamn {I} (X;Y)&{}=\summa _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p_ {(X,Y)}(x,y)\log {\frac {p_{(X,Y)}(x,y)}{p_{X}(x)p_{Y}(y)}}\ \&{}=\summa _{x\in {\mathcal {X}},y\in {\mathcal {Y}}}p_{(X,Y)}(x,y)\log {\frac { p_{(X,Y)}(x,y)}{p_{X}(x)}}-\summa _{x\in {\mathcal {X}},y\in {\mathcal {Y}} }p_{(X,Y)}(x,y)\log p_{Y}(y)\\&{}=\summa _{x\i {\mathcal {X}},y\i {\mathcal {Y}}}p_{X}(x)p_{Y\mid X=x}(y)\log p_{Y\mid X=x}(y)-\summa _{x\in {\mathcal { X}},y\in {\mathcal {Y}}}p_{(X,Y)}(x,y)\log p_{Y}(y)\\&{}=\summa _{x\in {\mathcal {X}}}p_{X}(x)\left(\summa _{y\in {\mathcal {Y}}}p_{Y\mid X=x}(y)\log p_{Y \mid X=x}(y)\right)-\summa _{y\in {\mathcal {Y}}}\left(\summa _{x\in {\mathcal {X}}}p_{(X ,Y)}(x,y)\right)\log p_{Y}(y)\\&{}=-\summa _{x\i {\mathcal {X}}}p_{X}(x) \mathrm {H} (Y\mid X=x)-\summa _{y\in {\mathcal {Y}}}p_{Y}(y)\log p_{Y}(y)\\&{} =-\mathrm {H} (Y\mid X)+\mathrm {H} (Y)\\&{}=\mathrm {H} (Y)-\mathrm {H} (Y\mitt X).\ \\end{aligned}}$

Bevisen för de andra identiteterna ovan är liknande. Beviset för det allmänna fallet (inte bara diskret) är liknande, med integraler som ersätter summor.

Intuitivt, om entropin $\mathrm {H} (Y)$ betraktas som ett mått på osäkerhet om en slumpvariabel, då $\mathrm {H} (Y\ mid X)$ är ett mått på vad $X$ inte säger om $Y$ . Detta är "mängden osäkerhet som återstår kring $Y$ efter att $X$ är känd", och därmed kan höger sida av den andra av dessa likheter läsas som "mängden osäkerhet i ${\ displaystyle Y}$ , minus mängden osäkerhet i $Y$ som finns kvar efter att $X$ är känd", vilket motsvarar "mängden osäkerhet i $Y$ som tas bort genom att veta $X$ ". Detta bekräftar den intuitiva innebörden av ömsesidig information som mängden information (det vill säga minskning av osäkerhet) som att känna till endera variabeln ger om den andra.

Observera att i det diskreta fallet $\mathrm {H} (Y\mid Y)=0$ och därför $\mathrm { H} (Y)=\operatörsnamn {I} (Y;Y)$ . Alltså ${\displaystyle \operatorname {I} (Y;Y)\geq \operatorname {I} (X;Y)} ,$ och man kan formulera grundprincipen att en variabel innehåller minst lika mycket information om sig själv som någon annan variabel kan ge.

Relation till Kullback–Leibler divergens

För gemensamt diskreta eller gemensamt kontinuerliga par $(X,Y)$ är ömsesidig information Kullback–Leibler-avvikelsen från produkten av marginalfördelningarna , $p_{X} \cdot p_{Y}$ , av den gemensamma fördelningen ${\displaystyle p_{(X,Y)}} ,$ dvs.

$\operatörsnamn {I} (X;Y)=D_{\text{KL}}\left(p_{ (X,Y)}\parallell p_{X}p_{Y}\right)$

Låt vidare $p_{(X,Y)}(x,y)=p_{X \mid Y=y}(x)*p_{Y}(y)$ vara den villkorliga massan eller densitetsfunktionen. Då har vi identiteten

$\operatörsnamn {I} (X;Y)=\mathbb {E} _{Y}\left[D_ {\text{KL}}\!\left(p_{X\mid Y}\parallel p_{X}\right)\right]$

Beviset för gemensamt diskreta slumpvariabler är följande:

${\begin{aligned}\operatörsnamn {I} (X;Y)&=\summa _{y\in {\mathcal {Y}}}\summa _{x\in {\mathcal {X}} }{p_{(X,Y)}(x,y)\log \left({\frac {p_{(X,Y)}(x,y)}{p_{X}(x)\,p_{ Y}(y)}}\right)}\\&=\summa _{y\in {\mathcal {Y}}}\summa _{x\in {\mathcal {X}}}p_{X\mid Y=y}(x)p_{Y}(y)\log {\frac {p_{X\mid Y=y}(x)p_{Y}(y)}{p_{X}(x)p_{ Y}(y)}}\\&=\summa _{y\in {\mathcal {Y}}}p_{Y}(y)\summa _{x\in {\mathcal {X}}}p_{ X\mid Y=y}(x)\log {\frac {p_{X\mid Y=y}(x)}{p_{X}(x)}}\\&=\summa _{y\in {\mathcal {Y}}}p_{Y}(y)\;D_{\text{KL}}\!\left(p_{X\mid Y=y}\parallel p_{X}\right)\\ &=\mathbb {E} _{Y}\left[D_{\text{KL}}\!\left(p_{X\mid Y}\parallel p_{X}\right)\right].\end{ Justerat}}$

På liknande sätt kan denna identitet fastställas för gemensamt kontinuerliga slumpvariabler.

Observera att Kullback–Leibler-divergensen här involverar enbart integration över värdena för slumpvariabeln $X$ och uttrycket $D_{\text{KL}} (p_{X\mid Y}\parallel p_{X})$ anger fortfarande en slumpvariabel eftersom $Y$ är slumpmässig. Sålunda kan ömsesidig information också förstås som förväntan av Kullback–Leibler-divergensen av den univariata fördelningen $p_{X}$ av $X$ från den villkorliga fördelningen $p_{ X\mid Y}$ av $X$ givet $Y$ : desto mer olika är fördelningarna $p_{X\mid Y}$ och $p_{X }$ är i genomsnitt, desto större informationsvinst .

Bayesiansk uppskattning av ömsesidig information

Om prover från en gemensam distribution finns tillgängliga, kan en Bayesiansk metod användas för att uppskatta den ömsesidiga informationen om den fördelningen. Det första arbetet att göra detta, som också visade hur man gör Bayesiansk uppskattning av många andra informationsteoretiska egenskaper förutom ömsesidig information, var. Efterföljande forskare har omarbetat och utökat denna analys. Se för ett färskt papper baserat på en tidigare speciellt anpassad för uppskattning av ömsesidig information i sig. föreslogs nyligen en uppskattningsmetod som tar hänsyn till kontinuerliga och multivariata utdata, ${\displaystyle Y} .$

Antaganden om oberoende

Kullback-Leibler-divergensformuleringen av den ömsesidiga informationen bygger på att man är intresserad av att jämföra $p(x,y)$ med den fullständigt faktoriserade yttre produkten $p(x)\cdot p(y)$ . I många problem, såsom icke-negativ matrisfaktorisering , är man intresserad av mindre extrema faktoriseringar; specifikt vill man jämföra $p(x,y)$ med en låg-rankad matrisapproximation i någon okänd variabel $w$ ; det vill säga i vilken grad man kan ha

$p(x,y)\approx \sum _{w}p^{\prime }(x, w)p^{\prime \prime }(w,y)$

Alternativt kan man vara intresserad av att veta hur mycket mer information $p(x,y)$ bär över sin faktorisering. I ett sådant fall ges den överskottsinformation som den fullständiga fördelningen $p(x,y)$ bär över matrisfaktoriseringen av Kullback-Leibler-divergensen

${\ displaystyle \operatorname {I} _{LRMA}=\summa _{y\in {\mathcal {Y}}}\summa _{x\in {\mathcal {X}}}{p(x,y)\log {\left({\frac {p(x,y)}{\sum _{w}p^{\prime }(x,w)p^{\prime \prime }(w,y)}}\right )}},}$

Den konventionella definitionen av den ömsesidiga informationen återvinns i det extrema fallet att processen $W$ endast har ett värde för $w$ .

Variationer

Flera varianter av ömsesidig information har föreslagits för att passa olika behov. Bland dessa finns normaliserade varianter och generaliseringar till fler än två variabler.

Metrisk

Många applikationer kräver en metrisk , det vill säga ett avståndsmått mellan par av punkter. Kvantiteten

${\begin{aligned}d(X,Y)&=\mathrm {H} (X,Y)- \operatörsnamn {I} (X;Y)\\&=\mathrm {H} (X)+\mathrm {H} (Y)-2\operatörsnamn {I} (X;Y)\\&=\mathrm { H} (X\mid Y)+\mathrm {H} (Y\mitt X)\\&=2\mathrm {H} (X,Y)-\mathrm {H} (X)-\mathrm {H} (Y)\end{aligned}}$

uppfyller egenskaperna hos en metrik ( triangelolikhet , icke-negativitet , ourskiljbarhet och symmetri). Detta avståndsmått är också känt som informationens variation .

Om $X,Y$ är diskreta slumpvariabler är alla entropitermer icke-negativa, så $0\leq d(X, Y)\leq \mathrm {H} (X,Y)$ och man kan definiera ett normaliserat avstånd

$D(X,Y)={\frac {d(X,Y)}{\mathrm {H} ( X,Y)}}\leq 1.$

Måttet $D$ är ett universellt mått, eftersom om något annat avståndsmått placerar $X$ och $Y$ i närheten, så kommer $D$ också att bedöma dem nära .

Att plugga in definitionerna visar det

$D(X,Y)=1-{\frac {\operatörsnamn {I} (X;Y)}{\mathrm {H} (X,Y)}}.$

Detta är känt som Rajski-distansen. I en mängdteoretisk tolkning av information (se figuren för villkorlig entropi ), är detta i praktiken Jaccard-avståndet mellan $X$ och $Y$ .

Till sist,

$D^{\prime }(X,Y)=1-{\frac { \operatörsnamn {I} (X;Y)}{\max \left\{\mathrm {H} (X),\mathrm {H} (Y)\right\}}}$

är också ett mått.

Villkorlig ömsesidig information

Huvudartikel: Villkorlig ömsesidig information

Ibland är det användbart att uttrycka den ömsesidiga informationen för två slumpvariabler som betingas av en tredje.

$\operatörsnamn {I} (X;Y| Z)=\mathbb {E} _{Z}[D_{\mathrm {KL} }(P_{(X,Y)|Z}\|P_{X|Z}\ibland P_{Y|Z})]$

För gemensamt diskreta slumpvariabler tar detta formen

$\operatorname {I} (X;Y|Z)=\summa _{z\in {\mathcal {Z}}}\summa _{y\in {\mathcal { Y}}}\summa _{x\in {\mathcal {X}}}{p_{Z}(z)\,p_{X,Y|Z}(x,y|z)\log \left[{ \frac {p_{X,Y|Z}(x,y|z)}{p_{X|Z}\,(x|z)p_{Y|Z}(y|z)}}\höger]} ,$

vilket kan förenklas som

$\operatorname {I} (X;Y|Z)=\summa _{z\in {\mathcal {Z}}}\summa _{y\in {\mathcal {Y}}}\summa _{ x\in {\mathcal {X}}}p_{X,Y,Z}(x,y,z)\log {\frac {p_{X,Y,Z}(x,y,z)p_{Z }(z)}{p_{X,Z}(x,z)p_{Y,Z}(y,z)}}.$

För gemensamt kontinuerliga stokastiska variabler tar detta formen

$\operatorname {I} (X;Y|Z)=\int _{\mathcal {Z}}\int _{\mathcal {Y}} \int _{\mathcal {X}}{p_{Z}(z)\,p_{X,Y|Z}(x,y|z)\log \left[{\frac {p_{X,Y| Z}(x,y|z)}{p_{X|Z}\,(x|z)p_{Y|Z}(y|z)}}\right]}dxdydz,$

vilket kan förenklas som

$\operatorname {I} (X;Y|Z)=\int _{\mathcal {Z}}\int _{\mathcal {Y}}\int _{\mathcal {X}}p_{X, Y,Z}(x,y,z)\log {\frac {p_{X,Y,Z}(x,y,z)p_{Z}(z)}{p_{X,Z}(x, z)p_{Y,Z}(y,z)}}dxdydz.$

Konditionering av en tredje slumpvariabel kan antingen öka eller minska den ömsesidiga informationen, men det är alltid sant

$\operatörsnamn {I} (X;Y|Z)\geq 0$

för diskreta, gemensamt fördelade slumpvariabler $X,Y,Z$ . Detta resultat har använts som en grundläggande byggsten för att bevisa andra ojämlikheter i informationsteorin .

Interaktionsinformation

Huvudartikel: Interaktionsinformation

Flera generaliseringar av ömsesidig information till mer än två slumpvariabler har föreslagits, såsom total korrelation (eller multi-information) och dubbel total korrelation . Uttrycket och studiet av multivariat högre grad av ömsesidig information uppnåddes i två till synes oberoende verk: McGill (1954) som kallade dessa funktioner "interaktionsinformation" och Hu Kuo Ting (1962). Interaktionsinformation definieras för en variabel enligt följande:

$\operatörsnamn {I} (X_{1})=\mathrm {H} (X_{1})$

och för $n>1,$

$\operatörsnamn {I} (X_{1};\,...\,;X_{n})=\operatörsnamn {I} (X_{1};\,...\,;X_{n -1})-\operatörsnamn {I} (X_{1};\,...\,;X_{n-1}\mid X_{n}).$

Vissa författare ändrar ordningen på termerna på höger sida av föregående ekvation, vilket ändrar tecknet när antalet slumpvariabler är udda. (Och i det här fallet blir uttrycket med en variabel det negativa av entropin.) Observera att

$I(X_{1};\ldots ;X_{n-1}\mid X_{n})=\mathbb {E} _{X_{n}}[D_{\mathrm {KL} }(P_ {(X_{1},\ldots ,X_{n-1})\mid X_{n}}\|P_{X_{1}\mid X_{n}}\otimes \cdots \otimes P_{X_{n -1}\mid X_{n}})].$

Multivariat statistiskt oberoende

De multivariata ömsesidiga informationsfunktionerna generaliserar det parvisa oberoendefallet som anger att $X_{1},X_{2}$ om och endast om $I(X_) {1};X_{2})=0$ , till godtyckliga talrika variabler. n variabler är ömsesidigt oberoende om och endast om de $2^{n}-n-1$ ömsesidiga informationsfunktionerna försvinner $I(X_ {1};\ldots ;X_{k})=0$ med $n\geq k\geq 2$ (sats 2). I denna mening $I(X_{1};\ldots ;X_{k})=0$ användas som ett förfinat statistiskt oberoendekriterium.

Ansökningar

För 3 variabler, Brenner et al. tillämpade multivariat ömsesidig information på neural kodning och kallade dess negativitet "synergi" och Watkinson et al. tillämpade det på genetiskt uttryck. För godtyckliga k variabler, Tapia et al. tillämpade multivariat ömsesidig information på genuttryck. Det kan vara noll, positivt eller negativt. Positiviteten motsvarar relationer som generaliserar de parvisa korrelationerna, nullitet motsvarar en förfinad uppfattning om oberoende, och negativitet upptäcker högdimensionella "emergent" relationer och klusteriserade datapunkter).

Ett högdimensionellt generaliseringsschema som maximerar den ömsesidiga informationen mellan den gemensamma fördelningen och andra målvariabler har visat sig vara användbart vid val av egenskaper .

Ömsesidig information används också inom området för signalbehandling som ett mått på likheten mellan två signaler. Till exempel är FMI-måttet ett prestandamått för bildfusion som använder ömsesidig information för att mäta mängden information som den sammanslagna bilden innehåller om källbilderna. Matlab - koden för detta mått finns på. Ett pythonpaket för att beräkna all multivariat ömsesidig information, villkorlig ömsesidig information, gemensamma entropier, totala korrelationer, informationsavstånd i en datauppsättning med n variabler är tillgänglig.

Riktad information

Riktad information , ${\displaystyle \operatorname {I} \left(X^{n}\to Y^{n}\right)} ,$ mäter mängden information som flödar från processen $X^{n}$ till $Y^{n}$ , där $X^{n}$ anger vektorn $X_{1},X_{2},...,X_{n}$ och $Y^{n}$ betecknar $Y_{1},Y_{2},...,Y_{n}$ . Termen riktad information myntades av James Massey och definieras som

$\operatorname {I} \left(X^{n}\to Y^{ n}\right)=\summa _{i=1}^{n}\operatörsnamn {I} \left(X^{i};Y_{i}\mid Y^{i-1}\right)$ .

Observera att om $n=1$ blir den riktade informationen den ömsesidiga informationen. Riktad information har många tillämpningar i problem där kausalitet spelar en viktig roll, såsom kanalkapacitet med återkoppling.

Normaliserade varianter

Normaliserade varianter av den ömsesidiga informationen tillhandahålls av koefficienterna för begränsning , osäkerhetskoefficient eller kompetens:

$C_{XY}={\frac {\operatörsnamn {I} (X;Y)}{\mathrm {H} (Y)}}~~~~{\mbox{and}}~~~~C_ {YX}={\frac {\operatörsnamn {I} (X;Y)}{\mathrm {H} (X)}}.$

De två koefficienterna har ett värde inom [0, 1], men är inte nödvändigtvis lika. I kan ett symmetriskt mått vara önskvärt såsom följande redundansmått

$R={\frac {\operatörsnamn {I} (X;Y)}{\mathrm {H} (X)+\mathrm {H} (Y)}}$

som uppnår ett minimum av noll när variablerna är oberoende och ett maximalt värde på

$R_{\max }={\frac {\min \left\{\mathrm {H} (X ),\mathrm {H} (Y)\right\}}{\mathrm {H} (X)+\mathrm {H} (Y)}}$

när en variabel blir helt överflödig med kunskapen om den andra. Se även Redundans (informationsteori) .

Ett annat symmetriskt mått är den symmetriska osäkerheten ( Witten & Frank 2005) , given av

$U(X,Y)=2R=2{\frac {\operatörsnamn {I} ( X;Y)}{\mathrm {H} (X)+\mathrm {H} (Y)}}$

som representerar det harmoniska medelvärdet av de två osäkerhetskoefficienterna $C_{XY},C_{YX}$ .

Om vi ​​betraktar ömsesidig information som ett specialfall av den totala korrelationen eller den dubbla totala korrelationen , är den normaliserade versionen respektive,

${\frac {\operatörsnamn {I} (X;Y)}{\min \left[\mathrm {H} (X ),\mathrm {H} (Y)\right]}}$ och ${\frac {\operatörsnamn {I} (X;Y)}{\mathrm {H} (X,Y)}}\;.$

Denna normaliserade version även känd som Information Quality Ratio (IQR) som kvantifierar mängden information för en variabel baserat på en annan variabel mot total osäkerhet:

$IQR(X,Y)=\operatörsnamn {E} [\ operatornamn {I} (X;Y)]={\frac {\operatörsnamn {I} (X;Y)}{\mathrm {H} (X,Y)}}={\frac {\summa _{x\ i X}\summa _{y\in Y}p(x,y)\log {p(x)p(y)}}{\summa _{x\in X}\summa _{y\in Y} p(x,y)\log {p(x,y)}}}-1$

Det finns en normalisering som härrör från att man först tänker på ömsesidig information som en analog till kovarians (sålunda är Shannon-entropi analog med varians ). Sedan beräknas den normaliserade ömsesidiga informationen i likhet med Pearsons korrelationskoefficient ,

${\frac {\operatörsnamn {I} (X;Y)}{\sqrt {\mathrm {H} (X)\mathrm {H} (Y)}}}\;.$

Viktade varianter

I den traditionella formuleringen av den ömsesidiga informationen,

$\operatörsnamn {I} (X; Y)=\summa _{y\in Y}\summa _{x\in X}p(x,y)\log {\frac {p(x,y)}{p(x)\,p(y )}},$

varje händelse eller objekt som anges av $(x,y)$ viktas med motsvarande sannolikhet $p(x,y)$ . Detta förutsätter att alla objekt eller händelser är likvärdiga förutom deras sannolikhet att inträffa. Men i vissa tillämpningar kan det vara så att vissa objekt eller händelser är mer betydelsefulla än andra, eller att vissa associationsmönster är mer semantiskt viktiga än andra.

Till exempel, den deterministiska mappningen $\{(1,1),(2,2),(3,3)\}$ kan ses som starkare än den deterministiska mappningen $\{(1,3),(2,1),(3,2) \}$ , även om dessa relationer skulle ge samma ömsesidiga information. Detta beror på att den ömsesidiga informationen inte alls är känslig för någon inneboende ordning i variabelvärdena ( Cronbach 1954 , Coombs, Dawes & Tversky 1970 , Lockhead 1970 ), och därför inte alls är känslig för formen av den relationella kartläggningen mellan de tillhörande variabler. Om man önskar att den förra relationen – som visar överensstämmelse om alla variabelvärden – bedöms som starkare än den senare relationen, så är det möjligt att använda följande viktade ömsesidiga information ( Guiasu 1977 ).

$\operatörsnamn {I} (X;Y)=\summa _{y\in Y}\summa _{x\in X}w(x,y)p(x,y)\log {\frac {p(x,y )}{p(x)\,p(y)}},$

vilket sätter en vikt $w(x,y)$ på sannolikheten för att varje variabelvärde ska inträffa samtidigt, $p(x,y)$ . Detta tillåter att vissa sannolikheter kan ha mer eller mindre betydelse än andra, vilket möjliggör kvantifiering av relevanta holistiska eller Prägnanzfaktorer . I exemplet ovan använder du större relativa vikter för $w(1,1)$ , $w(2,2)$ och $w(3,3)$ skulle ha effekten att bedöma större informativitet för relationen $\{(1,1) ),(2,2),(3,3)\}$ än för relationen $\{(1,3), (2,1),(3,2)\}$ , vilket kan vara önskvärt i vissa fall av mönsterigenkänning och liknande. Denna viktade ömsesidiga information är en form av viktad KL-Divergens, som är känd för att ta negativa värden för vissa indata, och det finns exempel där den viktade ömsesidiga informationen också tar negativa värden.

Justerad ömsesidig information

Huvudartikel: justerad ömsesidig information

En sannolikhetsfördelning kan ses som en partition av en uppsättning . Man kan då fråga sig: om en mängd var uppdelad slumpmässigt, vad skulle fördelningen av sannolikheter vara? Vad skulle förväntningsvärdet på den ömsesidiga informationen vara? Den justerade ömsesidiga informationen eller AMI subtraherar förväntningsvärdet för MI, så att AMI är noll när två olika distributioner är slumpmässiga, och en när två distributioner är identiska. AMI definieras i analogi med det justerade Rand-indexet för två olika partitioner i en uppsättning.

Absolut ömsesidig information

Med hjälp av idéerna om Kolmogorovs komplexitet kan man överväga den ömsesidiga informationen om två sekvenser oberoende av eventuell sannolikhetsfördelning:

$\operatörsnamn {I} _{K}(X;Y)=K(X)-K(X\mid Y).$

För att fastställa att denna kvantitet är symmetrisk upp till en logaritmisk faktor ( $\operatorname {I} _{K}(X;Y)\approx \ operatornamn {I} _{K}(Y;X)$ ) man kräver kedjeregeln för Kolmogorov-komplexitet ( Li & Vitányi 1997) . Approximationer av denna kvantitet via komprimering kan användas för att definiera ett avståndsmått för att utföra en hierarkisk klustring av sekvenser utan att ha någon domänkännedom om sekvenserna ( Cilibrasi & Vitányi 2005) .

Linjär korrelation

Till skillnad från korrelationskoefficienter, såsom produktmomentkorrelationskoefficienten, innehåller ömsesidig information information om allt beroende - linjärt och olinjärt - och inte bara linjärt beroende som korrelationskoefficientmåttet. Men i det snäva fallet att den gemensamma fördelningen för $X$ och $Y$ är en bivariat normalfördelning (vilket särskilt antyder att båda marginalfördelningarna är normalfördelade), finns det ett exakt samband mellan ${ \displaystyle \operatorname {I} }$ och korrelationskoefficienten $\rho$ ( Gel'fand & Yaglom 1957) .

$\operatorname {I} =-{\frac {1}{2}}\log \left(1-\rho ^{2}\right)$

Ekvationen ovan kan härledas enligt följande för en bivariat Gauss:

${\begin{aligned}{\begin{pmatrix}X_{1}\ \X_{2}\end{pmatrix}}&\sim {\mathcal {N}}\left({\begin{pmatrix}\mu _{1}\\\mu _{2}\end{pmatrix}} ,\Sigma \right),\qquad \Sigma ={\begin{pmatrix}\sigma _{1}^{2}&\rho \sigma _{1}\sigma _{2}\\\rho \sigma _ {1}\sigma _{2}&\sigma _{2}^{2}\end{pmatrix}}\\\mathrm {H} (X_{i})&={\frac {1}{2} }\log \left(2\pi e\sigma _{i}^{2}\right)={\frac {1}{2}}+{\frac {1}{2}}\log(2\ pi )+\log \left(\sigma _{i}\right),\quad i\in \{1,2\}\\\mathrm {H} (X_{1},X_{2})&= {\frac {1}{2}}\log \left[(2\pi e)^{2}|\Sigma |\right]=1+\log(2\pi )+\log \left(\sigma _{1}\sigma _{2}\right)+{\frac {1}{2}}\log \left(1-\rho ^{2}\right)\\\end{aligned}}$

Därför,

$\operatorname {I} \left(X_{1};X_{2}\right)=\mathrm {H} \left(X_{1}\right)+\mathrm {H} \left(X_{2}\right)-\mathrm {H} \left(X_{1},X_{2}\right)=-{\frac {1}{2}}\log \left(1-\rho ^{2}\right)$

För diskreta data

När $X$ och $Y$ är begränsade till att vara i ett diskret antal tillstånd, sammanfattas observationsdata i en beredskapstabell , med radvariabel ${\displaystyle X} ($ eller $i$ ) och kolumnvariabel $Y$ (eller $j$ ). Ömsesidig information är ett av måtten på association eller korrelation mellan rad- och kolumnvariablerna.

Andra mått på association inkluderar Pearsons chi-kvadratteststatistik , G- teststatistik, etc. Faktum är att med samma loggbas kommer ömsesidig information att vara lika med G-test log-sannolikhetsstatistik dividerat med $2N$ , där $N$ är provstorleken.

Ansökningar

I många applikationer vill man maximera ömsesidig information (och därmed öka beroenden), vilket ofta motsvarar att minimera villkorlig entropi . Exempel inkluderar:

• Inom sökmotorteknik används ömsesidig information mellan fraser och sammanhang som en funktion för k-betyder klustring för att upptäcka semantiska kluster (begrepp). Till exempel kan den ömsesidiga informationen för ett bigram beräknas som:

$MI(x,y )=\log {\frac {P_{X,Y}(x,y)}{P_{X}(x)P_{Y}(y)}}\approx \log {\frac {\frac {f_{ XY}}{B}}{{\frac {f_{X}}{U}}{\frac {f_{Y}}{U}}}}$

där $f_{XY}$ är antalet gånger som bigrammet xy förekommer i korpusen, $f_{X}$ är antalet gånger som unigrammet x förekommer i korpusen, B är det totala antalet bigram, och U är det totala antalet unigram.

• Inom telekommunikation är kanalkapaciteten lika med den ömsesidiga informationen , maximerad över alla ingångsdistributioner.
• Diskriminerande träningsprocedurer för dolda Markov-modeller har föreslagits baserat på kriteriet för maximal ömsesidig information (MMI).
• av sekundär RNA-struktur från en multipelsekvensinriktning .
• Fylogenetisk profilförutsägelse från parvis närvarande och försvinnande av funktionellt länkade gener .
• Ömsesidig information har använts som ett kriterium för funktionsval och funktionstransformationer i maskininlärning . Den kan användas för att karakterisera både relevansen och redundansen för variabler, till exempel valet av minimiredundansfunktion .
• Ömsesidig information används för att bestämma likheten mellan två olika klustringar av en datauppsättning. Som sådan ger det vissa fördelar jämfört med det traditionella Rand-indexet .
• Ömsesidig information om ord används ofta som en signifikansfunktion för beräkning av kollokationer inom korpuslingvistik . Detta har den extra komplexiteten att ingen ordinstans är en instans till två olika ord; snarare, man räknar fall där 2 ord förekommer intill eller i närheten; detta komplicerar beräkningen något, eftersom den förväntade sannolikheten för att ett ord ska förekomma inom $N$ ord i ett annat, går upp med $N$
• Ömsesidig information används vid medicinsk bildbehandling för bildregistrering . Givet en referensbild (till exempel en hjärnskanning) och en andra bild som måste placeras i samma koordinatsystem som referensbilden, deformeras denna bild tills den ömsesidiga informationen mellan den och referensbilden är maximerad.
• Detektering av fassynkronisering i tidsserieanalys .
• I infomax- metoden för neural-net och annan maskininlärning, inklusive den infomax-baserade Independent komponentanalysalgoritmen
• Genomsnittlig ömsesidig information i fördröjningsinbäddningsteorem används för att bestämma inbäddningsfördröjningsparametern .
• Ömsesidig information mellan gener i expressionsmikroarraydata används av ARACNE-algoritmen för rekonstruktion av gennätverk .
• Inom statistisk mekanik kan Loschmidts paradox uttryckas i termer av ömsesidig information. Loschmidt noterade att det måste vara omöjligt att bestämma en fysisk lag som saknar tidsomkastningssymmetri (t.ex. termodynamikens andra lag ) endast utifrån fysikaliska lagar som har denna symmetri. Han påpekade att Boltzmanns H-sats gjorde antagandet att partiklarnas hastigheter i en gas var permanent okorrelerade , vilket tog bort tidssymmetrin som är inneboende i H-satsen. Det kan visas att om ett system beskrivs av en sannolikhetstäthet i fasrymden , så innebär Liouvilles teorem att den gemensamma informationen (negativ för den gemensamma entropin) för fördelningen förblir konstant i tiden. Den gemensamma informationen är lika med den ömsesidiga informationen plus summan av all marginalinformation (negativ för marginalentropierna) för varje partikelkoordinat. Boltzmanns antagande går ut på att ignorera den ömsesidiga informationen i beräkningen av entropi, vilket ger den termodynamiska entropin (dividerat med Boltzmanns konstant).
• Den ömsesidiga informationen används för att lära sig strukturen av Bayesianska nätverk / dynamiska Bayesianska nätverk , vilket tros förklara orsakssambandet mellan slumpvariabler, vilket exemplifieras av GlobalMIT-verktygslådan: lära sig det globalt optimala dynamiska Bayesianska nätverket med kriteriet Mutual Information Test.
• Den ömsesidiga informationen används för att kvantifiera information som sänds under uppdateringsproceduren i Gibbs samplingsalgoritm .
• Populär kostnadsfunktion i beslutsträdsinlärning .
• Den ömsesidiga informationen används inom kosmologi för att testa inverkan av storskaliga miljöer på galaxegenskaper i Galaxy Zoo .
• Den ömsesidiga informationen användes i Solar Physics för att härleda soldifferentialrotationsprofilen , en restidsavvikelsekarta för solfläckar och ett tid-avståndsdiagram från mätningar av tysta sol
• Används i Invariant Information Clustering för att automatiskt träna neurala nätverksklassificerare och bildsegmenterare utan märkta data.

Se även

• Dataskillnad
• Punktvis ömsesidig information
• Quantum ömsesidig information
• Specifik information

Anteckningar

•    Baudot, P.; Tapia, M.; Bennequin, D.; Goaillard, JM (2019). "Topologisk informationsdataanalys" . Entropi . 21 (9). 869. arXiv : 1907.04242 . Bibcode : 2019Entrp..21..869B . doi : 10.3390/e21090869 . PMC 7515398 . S2CID 195848308 .
•   Cilibrasi, R.; Vitányi, Paul (2005). "Klustring genom komprimering" (PDF) . IEEE-transaktioner på informationsteori . 51 (4): 1523–1545. arXiv : cs/0312044 . doi : 10.1109/TIT.2005.844059 . S2CID 911 .
• Cronbach, LJ (1954). "Om den icke-rationella tillämpningen av informationsåtgärder i psykologin". I Quastler, Henry (red.). Informationsteori i psykologi: problem och metoder . Glencoe, Illinois: Fri press. s. 14–30.
• Coombs, CH; Dawes, RM; Tversky, A. (1970). Matematisk psykologi: en grundläggande introduktion . Englewood Cliffs, New Jersey: Prentice-Hall.
• Kyrka, Kenneth församling; Hanks, Patrick (1989). "Ordassociationsnormer, ömsesidig information och lexikografi" . Handlingar från Föreningen för datorlingvistiks 27:e årsmöte . 16 (1): 76–83. doi : 10.3115/981623.981633 .
•   Gel'fand, IM; Yaglom, AM (1957). "Beräkning av mängd information om en slumpmässig funktion som finns i en annan sådan funktion". American Mathematical Society Översättningar . Serie 2. 12 : 199–246. doi : 10.1090/trans2/012/09 . ISBN 9780821817124 . Engelsk översättning av originalet till Uspekhi Matematheskikh Nauk 12 (1): 3-52.
•   Guiasu, Silviu (1977). Informationsteori med tillämpningar . McGraw-Hill, New York. ISBN 978-0-07-025109-0 .
•   Li, Ming; Vitányi, Paul (februari 1997). En introduktion till Kolmogorovs komplexitet och dess tillämpningar . New York: Springer-Verlag . ISBN 978-0-387-94868-3 .
•   Lockhead, GR (1970). "Identifiering och formen av flerdimensionellt diskrimineringsrum". Journal of Experimental Psychology . 85 (1): 1–10. doi : 10.1037/h0029508 . PMID 5458322 .
•   David JC MacKay. Information Theory, Inference, and Learning Algorithms Cambridge: Cambridge University Press, 2003. ISBN 0-521-64298-1 (tillgänglig gratis online)
•   Haghighat, MBA; Aghagolzadeh, A.; Seyedarabi, H. (2011). "Ett mätvärde för bildfusion utan referens baserat på ömsesidig information om bildegenskaper". Datorer och elektroteknik . 37 (5): 744–756. doi : 10.1016/j.compeleceng.2011.07.012 . S2CID 7738541 .
• Athanasios Papoulis . Sannolikhet, slumpmässiga variabler och stokastiska processer, andra upplagan. New York: McGraw-Hill, 1984. (Se kapitel 15.)
•   Witten, Ian H. & Frank, Eibe (2005). Data Mining: Praktiska verktyg och tekniker för maskininlärning . Morgan Kaufmann, Amsterdam. ISBN 978-0-12-374856-0 .
•     Peng, HC; Long, F. & Ding, C. (2005). "Funktionsval baserat på ömsesidig information: kriterier för max-beroende, max-relevans och min-redundans" . IEEE-transaktioner på mönsteranalys och maskinintelligens . 27 (8): 1226–1238. CiteSeerX 10.1.1.63.5765 . doi : 10.1109/tpami.2005.159 . PMID 16119262 . S2CID 206764015 .
•    Andre S. Ribeiro; Stuart A. Kauffman; Jason Lloyd-Price; Björn Samuelsson & Joshua Socolar (2008). "Ömsesidig information i slumpmässiga booleska modeller av regulatoriska nätverk". Fysisk granskning E . 77 (1): 011901. arXiv : 0707.3642 . Bibcode : 2008PhRvE..77a1901R . doi : 10.1103/physreve.77.011901 . PMID 18351870 . S2CID 15232112 .
•   Wells, WM III; Viola, P.; Atsumi, H.; Nakajima, S.; Kikinis, R. (1996). "Multimodal volymregistrering genom maximering av ömsesidig information" (PDF) . Medicinsk bildanalys . 1 (1): 35–51. doi : 10.1016/S1361-8415(01)80004-9 . PMID 9873920 . Arkiverad från originalet (PDF) 2008-09-06 . Hämtad 2010-08-05 .
•   Pandey, Biswajit; Sarkar, Suman (2017). "Hur mycket vet en galax om sin storskaliga miljö?: Ett informationsteoretiskt perspektiv". Månatliga meddelanden från Royal Astronomical Society Letters . 467 (1): L6. arXiv : 1611.00283 . Bibcode : 2017MNRAS.467L...6P . doi : 10.1093/mnrasl/slw250 . S2CID 119095496 .