Lasso (statistik)

Den här artikeln handlar om statistik och maskininlärning. För annan användning, se Lasso (disambiguation) .

Inom statistik och maskininlärning är lasso ( operator för minsta absoluta krympning och urval ; även Lasso eller LASSO ) en regressionsanalysmetod som utför både variabelselektion och regularisering för att förbättra prediktionsnoggrannheten och tolkningsbarheten av den resulterande statistiska modellen . Det introducerades ursprungligen inom geofysiken och senare av Robert Tibshirani , som myntade termen.

Lasso formulerades ursprungligen för linjära regressionsmodeller . Detta enkla fall avslöjar en betydande mängd om estimatorn. Dessa inkluderar dess förhållande till åsregression och bästa delmängdsurval och sambanden mellan lassokoefficientuppskattningar och så kallad mjuk tröskel. Det avslöjar också att (liksom standard linjär regression) koefficientuppskattningarna inte behöver vara unika om kovariater är kolinjära .

Även om den ursprungligen definierades för linjär regression, kan lasso-regularisering lätt utökas till andra statistiska modeller inklusive generaliserade linjära modeller , generaliserade skattningsekvationer , proportionella riskmodeller och M-estimatorer . Lassos förmåga att utföra urval av delmängder förlitar sig på formen av begränsningen och har en mängd olika tolkningar, inklusive i termer av geometri , Bayesiansk statistik och konvex analys .

LASSO är nära besläktat med denoising av basjakt .

Historia

Lasso introducerades för att förbättra prediktionsnoggrannheten och tolkningsbarheten av regressionsmodeller. Den väljer en reducerad uppsättning av kända kovariater för användning i en modell.

Lasso utvecklades oberoende i geofysisk litteratur 1986, baserat på tidigare arbete som använde ℓ $\displaystyle \ell ^{1}}$ straff för både anpassning och bestraffning av koefficienterna. Statistikern Robert Tibshirani återupptäckte och populariserade den självständigt 1996, baserat på Breimans icke-negativa garrote.

Före lassot var den mest använda metoden för att välja kovariater stegvis urval . Det tillvägagångssättet förbättrar bara prediktionsnoggrannheten i vissa fall, till exempel när endast ett fåtal kovariater har ett starkt samband med resultatet. Men i andra fall kan det öka prediktionsfelet.

På den tiden var åsregression den mest populära tekniken för att förbättra prediktionsnoggrannheten. Ridge-regression förbättrar förutsägelsefelet genom att krympa summan av kvadraterna av regressionskoefficienterna till att vara mindre än ett fast värde för att minska överanpassning , men den utför inte samvariatval och hjälper därför inte till att göra modellen mer tolkningsbar.

Lasso uppnår båda dessa mål genom att tvinga summan av det absoluta värdet av regressionskoefficienterna att vara mindre än ett fast värde, vilket tvingar vissa koefficienter till noll, vilket utesluter dem från att påverka förutsägelse. Denna idé liknar åsregression, som också krymper storleken på koefficienterna; åsregression ställer dock inte koefficienterna till noll (och utför därför inte variabelval ).

Grundform

Minst kvadrater

Betrakta ett urval som består av N fall, som vart och ett består av p kovariater och ett enda utfall. Låt $y_{i}$ vara resultatet och $x_{i}:=(x_{1},x_{ 2},\ldots ,x_{p})_{i}^{T}$ vara kovariatvektorn för det i: ^te fallet. Då är målet med lasso att lösa

$\min _{\beta _{0},\beta }\left\{\sum _{i=1}^{N}(y_{i}-\beta _{0}-x_{i} ^{T}\beta )^{2}\right\}{\text{ med förbehåll för }}\summa _{j=1}^{p}|\beta _{j}|\leq t.$

Här är $\beta _{0}$ den konstanta koefficienten, $\beta :=(\beta _{1},\beta _ {2},\ldots ,\beta _{p})$ är koefficientvektorn, och $t$ är en fördefinierad fri parameter som bestämmer graden av regularisering.

Låter $X$ vara den kovariata matrisen, så att $X_{ij}=(x_{i})_{j}$ och $x_ {i}^{T}$ är den i: ^te raden av $X$ , uttrycket kan skrivas mer kompakt som

$\min _{\beta _{0},\beta }\left\{\left\| y-\beta _{0}-X\beta \right\|_{2}^{2}\right\}{\text{ med förbehåll för }}\|\beta \|_{1}\leq t,$

där $\|u\|_{p}=\left(\summa _{i=1}^{N}| u_{i}|^{p}\right)^{1/p}$ är standard $\ell ^{p}$ norm .

Betecknar det skalära medelvärdet av datapunkterna $x_{i}$ med ${\bar {x}}$ och medelvärdet av svarsvariablerna $y_{i}$ med ${\bar {y}}$ , den resulterande uppskattningen för $\beta _{0}$ är ${\displaystyle {\hat {\beta } }_{0}={\bar {y}}-{\bar {x}}^{T}\beta } ,$ så att

$y_{i}-{\hat {\beta }}_{0}-x_{i}^{T}\beta =y_{i}-({\bar {y}}-{\bar {x}} ^{T}\beta )-x_{i}^{T}\beta =(y_{i}-{\bar {y}})-(x_{i}-{\bar {x}})^{ T}\beta ,$

och därför är det standard att arbeta med variabler som har gjorts noll-medelvärde. Dessutom är kovariaterna vanligtvis standardiserade $\textstyle \left(\sum _{i=1}^{N}x_{i}^{2}=1\ höger)$ så att lösningen inte beror på mätskalan.

Det kan vara bra att skriva om

$\min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\|yX\beta \right\|_{2} ^{2}\right\}{\text{ med förbehåll för }}\|\beta \|_{1}\leq t.$

i den så kallade lagrangiska formen

$\min _{\beta \in \mathbb {R} ^{p}}\left\{{\ frac {1}{N}}\left\|yX\beta \right\|_{2}^{2}+\lambda \|\beta \|_{1}\right\}$

där det exakta förhållandet mellan $t$ och $\lambda$ är databeroende.

Ortonormala kovariater

Några grundläggande egenskaper hos lassoskattaren kan nu övervägas.

Antag först att kovariaterna är ortonormala så att ${\displaystyle x_{i}^{T}x_{j}=\delta _{ij}} ,$ där $\ delta _{ij}$ är Kronecker-deltatet , eller motsvarande $X^{T}X=I$ , då kan man med hjälp av subgradientmetoder visa att

${\begin{aligned}{\hat {\beta }}_{j}={}&S_{N\lambda }({\hat {\beta}}_{j}^{\text{OLS }})={\hat {\beta }}_{j}^{\text{OLS}}\max \left(0,1-{\frac {N\lambda }{|{\hat {\beta } }_{j}^{\text{OLS}}|}}\right)\\&{\text{ där }}{\hat {\beta }}^{\text{OLS}}=(X^{ T}X)^{-1}X^{T}y=X^{T}y\end{aligned}}$

$S_{\alpha }$ hänvisas till som den mjuka tröskeloperatorn , eftersom den översätter värden mot noll (gör dem exakt noll om de är tillräckligt små) istället för att sätta mindre värden till noll och lämna större orörda som den hårda tröskeloperatorn , ofta betecknad $H_{\alpha }$ , skulle.

Vid åsregression är målet att minimera

$\min _{\beta \in \mathbb {R} ^{p}}\left\{{ \frac {1}{N}}\|yX\beta \|_{2}^{2}+\lambda \|\beta \|_{2}^{2}\right\}$

Använder $X^{T}X=I$ och åsregressionsformeln: ${\displaystyle {\hat { \beta }}=\left((X^{T}X)+N\lambda I\right)^{-1}X^{T}y} , det ger$ :

${\hat {\beta }}_{j}=(1+N\lambda )^{-1}{\hat {\beta}}_{j}^{\text{OLS}}.$

Ridge-regression krymper alla koefficienter med en enhetlig faktor på $(1+N\lambda )^{-1}$ och sätter inga koefficienter till noll. .

Det kan också jämföras med regression med val av bästa delmängd , där målet är att minimera

$\min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\|yX\beta \right\|_{2}^{2}+\lambda \|\beta \|_{0}\right\}$

där $\|\cdot \|_{0}$ är " $\ell ^{0}$ -normen", som definieras som $\|z \|=m$ om exakt m komponenter i z inte är noll. I det här fallet kan det visas

${\hat {\beta }}_{j}=H_{\sqrt {N\lambda }}\left({\hat {\beta}}_{j}^{\text{OLS}}\right)={\hat {\beta}}_{j}^{\text{ OLS}}\mathrm {I} \left(\left|{\hat {\beta}}_{j}^{\text{OLS}}\right|\geq {\sqrt {N\lambda }}\right )$

där $H_{\alpha }$ är den så kallade hårda tröskelfunktionen och $\mathrm {I}$ är en indikatorfunktion (den är 1 om dess argument är sant och 0 annars).

Därför delar lassouppskattningarna egenskaper hos både ås- och bästa delmängdselektionsregression eftersom de båda krymper storleken på alla koefficienter, som åsregression, och ställer några av dem till noll, som i det bästa delmängdselektionsfallet. Dessutom, medan åsregression skalar alla koefficienter med en konstant faktor, översätter lasso istället koefficienterna mot noll med ett konstant värde och sätter dem till noll om de når det.

Korrelerade kovariater

I ett specialfall är två kovariater, säg j och k , identiska för varje observation, så att ${\displaystyle x_{(j)}=x_{(k)}} ,$ där $x_{(j),i}=x_{(k),i}$ . Då är värdena för $\beta _{j}$ och $\beta _{k}$ som minimerar lassoobjektivfunktionen inte unikt bestämda. Faktum är att om några ${\hat {\beta }}$ där ${\hat {\beta }}_{j}{\hat {\beta } }_{k}\geq 0$ , då om $s\in [0,1]$ ersätter ${\hat {\beta }}_{j}$ av ${\displaystyle s({\hat {\beta }}_{j}+{\hat {\beta }}_{k})} och$ β $\displaystyle {\hat {\beta }}_{k}}$ av $(1-s)({\hat {\beta }}_{j}+ {\hat {\beta }}_{k})$ , samtidigt som alla andra ${\hat {\beta }}_{i}$ hålls fasta, ger en ny lösning, så lassomålet Funktionen har då ett kontinuum av giltiga minimerare. Flera varianter av lassot, inklusive elastisk nätreglering , har utformats för att åtgärda denna brist.

Allmän form

Lasso-regularisering kan utvidgas till andra objektiva funktioner såsom de för generaliserade linjära modeller , generaliserade skattningsekvationer , proportionella riskmodeller och M-estimatorer . Med tanke på den objektiva funktionen

${\frac {1}{N}}\summa _{i=1}^{N}f(x_{i} ,y_{i},\alpha ,\beta )$

den lasso-reguljäriserade versionen av estimatorn är lösningen på

$\min _{\alpha ,\beta }{\frac {1} {N}}\summa _{i=1}^{N}f(x_{i},y_{i},\alpha ,\beta ){\text{ med förbehåll för }}\|\beta \|_{ 1}\leq t$

där endast $\beta$ straffas medan $\alpha$ är fri att ta vilket tillåtet värde som helst, precis som $\beta _{0}$ inte straffades i grundfallet.

Tolkningar

Geometrisk tolkning

Former av begränsningsregionerna för lasso- och åsregression.

Lasso kan sätta koefficienter till noll, medan den ytligt likartade åsregressionen inte kan. Detta beror på skillnaden i formen på deras begränsningsgränser. Både lasso- och åsregression kan tolkas som att samma objektiva funktion minimeras

$\min _{\beta _{0},\beta }\left\{{\frac {1}{N}}\ vänster\|y-\beta _{0}-X\beta \right\|_{2}^{2}\right\}$

men med hänsyn till olika begränsningar: $\|\beta \|_{1}\leq t$ för lasso och $\|\beta \|_ {2}^{2}\leq t$ för ås. Figuren visar att begränsningsområdet som definieras av $\ell ^{1}$ -normen är en kvadrat som roteras så att dess hörn ligger på axlarna (i allmänhet en korspolytop ), medan regionen som definieras av $\ell ^{2}$ norm är en cirkel (i allmänhet en n -sfär ), som är rotationsinvariant och därför inte har några hörn. Som framgår av figuren kommer sannolikt ett konvext objekt som tangerar gränsen, såsom linjen som visas, att möta ett hörn (eller en högre dimensionell motsvarighet) av en hyperkub, för vilken vissa komponenter i β {\ $\ beta }$ är identiskt noll, medan i fallet med en n -sfär, särskiljs inte punkterna på gränsen för vilka några av komponenterna i $\beta$ är noll från de andra och det konvexa objektet är inte längre kommer sannolikt att kontakta en punkt där vissa komponenter i $\beta$ är noll än en för vilken ingen av dem är det.

Gör λ lättare att tolka med en kompromiss mellan precision och enkelhet

Lasso kan skalas om så att det blir lätt att förutse och påverka graden av krympning som är förknippad med ett givet värde på $\lambda$ . Det antas att $X$ är standardiserad med z-poäng och att $y$ är centrerad (noll medelvärde). Låt $\beta _{0}$ representera de hypoteserade regressionskoefficienterna och låt $b_{OLS}$ hänvisa till de dataoptimerade vanliga minsta kvadraters lösningar. Vi kan sedan definiera Lagrangian som en avvägning mellan noggrannheten i stickprovet för de dataoptimerade lösningarna och enkelheten att hålla sig till de hypotesvärden. Detta resulterar i

$\min _{\beta \in \mathbb {R} ^{p}}\left\{{\frac {(yX\beta )'(yX\beta )}{(yX\beta _ {0})'(yX\beta _{0})}}+2\lambda \sum _{i=1}^{p}{\frac {|\beta _{i}-\beta _{0, i}|}{q_{i}}}\right\}$

där $q_{i}$ anges nedan. Den första bråkdelen representerar relativ noggrannhet, den andra bråkdelen relativ enkelhet och $\lambda$ balanserar mellan de två.

Lösningsvägar för $\ell _{1}$ -normen och $\ell _{2}$ -normen när $b_{OLS}=2$ och $\beta _{0}=0$

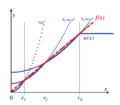
Givet en enda regressor kan relativ enkelhet definieras genom att specificera $q_{i}$ som $|b_{OLS}-\beta _{0}|$ , vilket är den maximala mängden avvikelse från $\beta _{0}$ när $\lambda =0$ . Om vi ​​antar att $\beta _{0}=0$ kan lösningsvägen definieras i termer av $R^{2}$ :

$b_{\ell _{1}}={\begin{cases}(1-\lambda /R^{2})b_{OLS}&{\mbox{if }}\lambda \leq R^{ 2},\\0&{\mbox{if }}\lambda >R^{2}.\end{cases}}$

Om $\lambda =0$ används den vanliga minsta kvadratlösningen (OLS). Det antagna värdet på $\beta _{0}=0$ väljs om $\lambda$ är större än $R^{2}$ . Dessutom, om $R^{2}=1$ , så representerar $\lambda$ det proportionella inflytandet av $\beta _{0}=0$ . Med andra ord, $\lambda \times 100\%$ mäter procentuellt den minimala mängden påverkan av det antagna värdet i förhållande till den dataoptimerade OLS-lösningen.

Om en $\ell _{2}$ -norm används för att straffa avvikelser från noll givet en enskild regressor, ges lösningsvägen av

$b_{\ell _{2}}={\bigg (}1+{\frac {\lambda }{ R^{2}(1-\lambda )}}{\bigg )}^{-1}b_{OLS}$ . Som $b_{\ell _{1}}$ , $b_{\ell _{2}}$ rör sig i punktens riktning $(\lambda =R^{2},b=0)$ när $\lambda$ är nära noll; men till skillnad från ${\displaystyle b_{\ell _{1}}} minskar$ påverkan av $R^{2}$ i $b_{\ell _{2}}$ om $\lambda$ ökar (se figur). Givet flera regressorer, bestäms det ögonblick då en parameter aktiveras (dvs tillåts avvika från $\beta _{0}$ ) också av en regressors bidrag till $R^{2}$ noggrannhet. Först,

$R^{2}=1-{\frac {(y-Xb)'(y-Xb)}{(yX\beta _{0})'(yX\beta _{0})}}.$

En $R^{2}$ på 75 % betyder att noggrannheten i urvalet förbättras med 75 % om de obegränsade OLS-lösningarna används istället för de hypoteserade $\beta _{0}$ -värdena. Det individuella bidraget för att avvika från varje hypotes kan beräknas med $p$ x $p$ -matrisen

$R^{\otimes }=(X'{\tilde { y}}_{0})(X'{\tilde {y}}_{0})'(X'X)^{-1}({\tilde {y}}_{0}'{\tilde {y}}_{0})^{-1},$

där ${\tilde {y}}_{0}=yX\beta _{0}$ . Om $b=b_{OLS}$ när $R^{2}$ beräknas, så summerar de diagonala elementen i $R^{\otimes }$ till $R^{2}$ . De diagonala ${\displaystyle R^{\otimes }}-$ värdena kan vara mindre än 0 eller, mer sällan, större än 1. Om regressorer är okorrelerade, då det $i^{th}$ diagonalelementet av $R^{\otimes }$ motsvarar helt enkelt $r^{2}$ -värdet mellan $x_{i}$ och $y$ .

En omskalad version av det adaptiva lassot av kan erhållas genom att ställa in $q_{{\mbox{adaptiv lasso}},i}=|b_{OLS,i}-\beta _{0,i}|$ . Om regressorer är okorrelerade, ges det ögonblick då $i^{th}$ aktiveras av det $i^{th}$ diagonalelementet i $R^ {\otimes }$ . Om vi ​​antar för enkelhetens skull att $\beta _{0}$ är en vektor med nollor,

$b_{i}={\begin{cases}(1-\lambda /R_{ii}^{\otimes })b_{OLS,i}&{\mbox{if }}\lambda \leq R_{ ii}^{\otimes },\\0&{\mbox{if }}\lambda >R_{ii}^{\otimes }.\end{cases}}$

Det vill säga, om regressorer är okorrelerade, anger $\lambda$ återigen den minimala påverkan av $\beta _{0}$ . Även när regressorer är korrelerade, inträffar första gången som en regressionsparameter aktiveras när $\lambda$ är lika med det högsta diagonala elementet i $R^{\otimes }$ .

Dessa resultat kan jämföras med en omskalad version av lassot genom att definiera $q_{{\mbox{lasso}},i}={\frac {1}{p}}\sum _{l}|b_{OLS,l}-\beta _{0,l}|$ , vilket är den genomsnittliga absoluta avvikelsen för $b_{OLS}$ från $\beta _{0}$ . Om man antar att regressorer är okorrelerade, så ges tidpunkten för aktivering av ${\displaystyle i^{th}} regressorn av$

${\tilde {\lambda }}_{{\text{lasso}},i}={\frac {1}{p}}{\sqrt {R_{i}^{\otimes }}}\ summa _{l=1}^{p}{\sqrt {R_{l}^{\otimes }}}.$

För $p=1$ ges aktiveringsmomentet återigen av ${\tilde {\lambda }}_{{\text{lasso}},i }=R^{2}$ . Om $\beta _{0}$ är en vektor med nollor och en delmängd av $p_{B}$ är relevanta parametrar lika ansvariga för en perfekt passning av $R^ {2}=1$ , då aktiveras denna delmängd vid ett $\lambda$ -värde på ${\frac {1}{p}}$ . Momentet för aktivering av en relevant regressor är då lika med ${\frac {1}{p}}{\frac {1}{\sqrt {p_{B} }}}p_{B}{\frac {1}{\sqrt {p_{B}}}}={\frac {1}{p}}$ . Med andra ord, inkluderingen av irrelevanta regressorer fördröjer det ögonblick då relevanta regressorer aktiveras av detta omskalade lasso. Det adaptiva lassot och lassot är specialfall av en '1ASTc'-estimator. Den senare grupperar bara parametrar om den absoluta korrelationen mellan regressorer är större än ett användarspecificerat värde.

Bayesiansk tolkning

Laplace-fördelningarna är kraftigt toppade vid sitt medelvärde med mer sannolikhetstäthet koncentrerad där jämfört med en normalfördelning.

Precis som åsregression kan tolkas som linjär regression för vilken koefficienterna har tilldelats normala tidigare fördelningar , kan lasso tolkas som linjär regression för vilken koefficienterna har Laplace-fördelningar . Laplacefördelningen har en skarp topp vid noll (dess första derivata är diskontinuerlig vid noll) och den koncentrerar sin sannolikhetsmassa närmare noll än vad normalfördelningen gör. Detta ger en alternativ förklaring till varför lasso tenderar att sätta vissa koefficienter till noll, medan åsregression inte gör det.

Konvex avslappningstolkning

Lasso kan också ses som en konvex relaxation av det bästa delmängdselektionsregressionsproblemet, vilket går ut på att hitta delmängden av $\leq k$ kovariater som resulterar i det minsta värdet av objektivfunktionen för vissa fasta $k\leq n$ , där n är det totala antalet kovariater. " $\ell ^{0}$ -normen", $\|\cdot \|_{0}$ , (antalet poster som inte är noll i en vektor), är det begränsande fallet för " $\ell ^{p}$ normer", av formen ${\displaystyle \textstyle \|x\|_ {p}=\left(\sum _{i=1}^{n}|x_{j}|^{p}\right)^{1/p}} (där citattecken betyder att dessa inte riktigt$ är normer för $p<1$ eftersom $\|\cdot \|_{p}$ inte är konvex för $p<1$ , så triangelolikheten håller inte). Därför, eftersom p = 1 är det minsta värdet för vilket " ${\displaystyle \ell ^{p}}-$ normen" är konvex (och därför faktiskt en norm), är lasso i någon mening den bästa konvexa approximationen till det bästa urvalsproblemet för delmängd, eftersom regionen som definieras av $\|x\|_{1}\leq t$ är det konvexa skrovet i regionen som definieras av ${\ displaystyle \|x\|_{p}\leq t}$ för $p<1$ .

Generaliseringar

Lasso-varianter har skapats för att avhjälpa begränsningar i den ursprungliga tekniken och för att göra metoden mer användbar för särskilda problem. Nästan alla dessa fokuserar på att respektera eller utnyttja beroenden bland kovariaterna.

Elastisk nettoregularisering lägger till en ytterligare åsregressionsliknande straff som förbättrar prestandan när antalet prediktorer är större än urvalsstorleken, gör att metoden kan välja starkt korrelerade variabler tillsammans och förbättrar den totala prediktionsnoggrannheten.

Grupplasso tillåter grupper av relaterade kovariater att väljas som en enda enhet, vilket kan vara användbart i inställningar där det inte är meningsfullt att inkludera vissa kovariater utan andra. Ytterligare utökningar av grupplasso utför variabelval inom individuella grupper (gles grupplasso) och tillåter överlappning mellan grupper (överlappsgrupplasso).

Fused lasso kan redogöra för de rumsliga eller tidsmässiga egenskaperna hos ett problem, vilket resulterar i uppskattningar som bättre matchar systemstrukturen. Lasso-regulariserade modeller kan anpassas med hjälp av tekniker inklusive subgradientmetoder , minsta vinkelregression (LARS) och proximala gradientmetoder . Att fastställa det optimala värdet för regulariseringsparametern är en viktig del för att säkerställa att modellen fungerar bra; det väljs vanligtvis med hjälp av korsvalidering .

Elastiskt nät

Huvudartikel: Elastisk nettoreglering

2005 introducerade Zou och Hastie det elastiska nätet . När p > n (antalet kovariater är större än urvalsstorleken) kan lasso endast välja n kovariater (även när fler är associerade med resultatet) och den tenderar att välja en kovariat från vilken uppsättning av högkorrelerade kovariater som helst. Dessutom, även när n > p , tenderar åsregression att prestera bättre givet starkt korrelerade kovariater.

Det elastiska nätet förlänger lasso genom att lägga till ytterligare $\ell ^{2}$ strafftid som ger

$\min _{\beta \in \mathbb {R} ^{pbb {R} }}\left\{\left\|yX\beta \right\|_{2}^{2}+\lambda _{1}\|\beta \|_{1}+\lambda _{2}\ |\beta \|_{2}^{2}\right\},$

vilket motsvarar att lösa

${\begin{aligned}\min _{\beta _{0},\beta}\left\{\left\|y-\beta _{0}-X\beta \right\|_{2 }^{2}\right\}&{\text{ med förbehåll för }}(1-\alpha )\|\beta \|_{1}+\alpha \|\beta \|_{2}^{2 }\leq t,\\&{\text{ där }}\alpha ={\frac {\lambda _{2}}{\lambda _{1}+\lambda _{2}}}.\end{aligned }}$

Detta problem kan skrivas i en enkel lassoform

$\displaystyle \min _{\beta ^{*}\in \mathbb }}\left\{\left\|y^{*}-X^{*}\beta ^{*}\right\|_{2}^{2}+\lambda ^{*}\|\beta ^{*}\|_{1}\right\}}$

uthyrning

$X_{(n+p)\ gånger p}^{*} =(1+\lambda _{2})^{-1/2}{\binom {X}{\lambda _{2}^{1/2}I_{p\times p}}}$ , $y_{(n+p)}^{*}={\binom {y}{0^{p}}} ,\qquad \lambda ^{*}={\frac {\lambda _{1}}{\sqrt {1+\lambda _{2}}}}$ , $\beta ^{*}={\sqrt {1+\lambda _{2}}}\beta .$

Sedan ${\displaystyle {\hat {\beta }}={\frac {{\hat {\beta }}^{*}}{\sqrt {1+\lambda _{ 2}}}}} ,$ vilket, när kovariaterna är ortogonala mot varandra, ger

${\hat {\beta }}_{j}={\frac {{\hat {\beta}}_{j}^{\text{*,OLS}}}{\sqrt {1+\ lambda _{2}}}}\max \left(0,1-{\frac {\lambda ^{*}}{\left|{\hat {\beta}}_{j}^{\text{* ,OLS}}\right|}}\right)={\frac {{\hat {\beta}}_{j}^{\text{OLS}}}{1+\lambda _{2}}}\ max \left(0,1-{\frac {\lambda _{1}}{\left|{\hat {\beta}}_{j}^{\text{OLS}}\right|}}\right )=(1+\lambda _{2})^{-1}{\hat {\beta }}_{j}^{\text{lasso}}.$

Så resultatet av den elastiska nettostraffen är en kombination av effekterna av lasso- och ridge-straffen.

För att återgå till det allmänna fallet, det faktum att strafffunktionen nu är strikt konvex betyder att om $x_{(j)}=x_{(k)}$ , ${\displaystyle {\hat {\beta }}_{j}={\hat {\beta }}_{k}} ,$ vilket är en förändring från lasso. I allmänhet, om ${\hat {\beta }}_{j}{\hat {\beta _{k}}}>0$

${\frac {|{\hat {\beta }}_{j}-{\hat {\ beta _{k}}}|}{\|y\|}}\leq \lambda _{2}^{-1}{\sqrt {2(1-\rho _{jk})}},{\ text{ där }}\rho =X^{t}X,$

är provkorrelationsmatrisen eftersom $x$ är normaliserade.

Därför tenderar högkorrelerade kovariater att ha liknande regressionskoefficienter, med graden av likhet beroende på både $\|y\|_{1}$ och $\lambda _{2}$ , som skiljer sig från lasso. Detta fenomen, där starkt korrelerade kovariater har liknande regressionskoefficienter, kallas för grupperingseffekten. Gruppering är önskvärt eftersom det i tillämpningar som att knyta gener till en sjukdom är att hitta alla associerade kovariater att föredra, snarare än att välja en från varje uppsättning av korrelerade kovariater, som lasso ofta gör. Att välja endast en från varje grupp resulterar dessutom vanligtvis i ökat prediktionsfel, eftersom modellen är mindre robust (vilket är anledningen till att åsregression ofta överträffar lasso).

Grupplasso

2006 introducerade Yuan och Lin grupplassot för att tillåta fördefinierade grupper av kovariater att gemensamt väljas in i eller ut ur en modell. Detta är användbart i många sammanhang, kanske mest uppenbart när en kategorisk variabel kodas som en samling binära kovariater. I det här fallet kan grupplasso säkerställa att alla variabler som kodar för den kategoriska kovariaten inkluderas eller exkluderas tillsammans. En annan miljö där gruppering är naturlig är i biologiska studier. Eftersom gener och proteiner ofta ligger i kända vägar, kan vilka vägar som är relaterade till ett utfall vara mer betydelsefulla än om enskilda gener är det. Objektivfunktionen för grupplassot är en naturlig generalisering av standardlassomålet

$\min _{\beta \in \mathbb {R} ^{p}}\left\{\left\|y-\summa _{j=1}^{J}X_{j}\ beta _{j}\right\|_{2}^{2}+\lambda \sum _{j=1}^{J}\|\beta _{j}\|_{K_{j}}\ höger\},\qquad \|z\|_{K_{j}}=(z^{t}K_{j}z)^{1/2}$

där designmatrisen $X$ och kovariatvektorn $\beta$ har ersatts av en samling designmatriser $X_{j}$ och kovariatvektorerna $\beta _ {j}$ , en för var och en av J-grupperna. Dessutom är strafftermen nu en summa över $\ell ^{2}$ normer definierade av de positiva definitiva matriserna $K_{j}$ . Om varje kovariat är i sin egen grupp och ${\displaystyle K_{j}=I} ,$ reduceras detta till standardlassot, medan om det bara finns en enda grupp och $K_{ 1}=I$ , det reduceras till åsregression. Eftersom straffet minskar till en $\ell ^{2}$ -norm på de delrymden som definieras av varje grupp, kan den inte välja ut endast några av kovariaterna från en grupp, precis som åsregression inte kan. Men eftersom straffet är summan över de olika delrumsnormerna, som i standardlassot, har begränsningen några icke-differentiella punkter, som motsvarar att vissa delrum är identiskt noll. Därför kan den ställa in koefficientvektorerna som motsvarar vissa delrum till noll, medan andra bara krymper. Det är dock möjligt att utöka grupplassot till det så kallade sparse grupplassot, som kan välja individuella kovariater inom en grupp, genom att lägga till ytterligare $\ell ^{1}$ straff till varje gruppdelrum. En annan förlängning, grupplasso med överlappning tillåter att kovariater delas mellan grupper, t.ex. om en gen skulle förekomma i två vägar.

Smält lasso

I vissa fall kan fenomenet som studeras ha en viktig rumslig eller tidsmässig struktur som måste beaktas vid analys, såsom tidsserier eller bildbaserad data. 2005 introducerade Tibshirani och kollegor det sammansmälta lassot för att utöka användningen av lasso till denna typ av data. Den sammansmälta lassoobjektivfunktionen är

${\begin{aligned}&\min _{\beta }\left\{{\frac {1}{N}}\summa _{i=1}^{N}\left(y_{i} -x_{i}^{t}\beta \right)^{2}\right\}\\[4pt]&{\text{ med förbehåll för }}\summa _{j=1}^{p}|\ beta _{j}|\leq t_{1}{\text{ och }}\summa _{j=2}^{p}|\beta _{j}-\beta _{j-1}|\leq t_{2}.\end{aligned}}$

Den första begränsningen är lasso-begränsningen, medan den andra direkt straffar stora förändringar med avseende på den tidsmässiga eller rumsliga strukturen, vilket tvingar koefficienterna att variera smidigt för att återspegla systemets underliggande logik. Clustered lasso är en generalisering av fused lasso som identifierar och grupperar relevanta kovariater baserat på deras effekter (koefficienter). Den grundläggande idén är att straffa skillnaderna mellan koefficienterna så att ettor som inte är noll kluster. Detta kan modelleras med hjälp av följande regularisering:

$\sum _{i<j}^{p}|\beta _{i}-\beta _{j}|\leq t_{2}.$

Däremot kan variabler klustras i högkorrelerade grupper, och sedan kan en enda representativ kovariat extraheras från varje kluster.

Algoritmer finns som löser det sammansmälta lassoproblemet, och några generaliseringar av det. Algoritmer kan lösa det exakt i ett begränsat antal operationer.

Kvasinormer och broregression

Ett exempel på en PQSQ (bitvis kvadratisk funktion av subquadratisk tillväxt) potentialfunktion $u(x)$ ; här är majorantfunktionen $f(x)=x$ ; potentialen definieras med trimning efter $r_{3}$ .

Ett exempel på hur effektiv PQSQ-reguljär regression fungerar precis som $\ell ^{1}$ -normlasso.

Lasso, elastiskt nät, grupp och smält lasso konstruerar strafffunktionerna från $\ell ^{1}$ och $\ell ^{2}$ -normerna (med vikter, om det behövs). Bryggegressionen använder allmänna $\ell ^{p}$ normer ( $p\geq 1$ ) och kvasinormer ( $0<p<1$ ). Till exempel, för p =1/2 är analogen till lassoobjektiv i lagrangisk form att lösa

$\min _{\beta \in \mathbb {R} ^{p}}\left\ {{\frac {1}{N}}\left\|yX\beta \right\|_{2}^{2}+\lambda {\sqrt {\|\beta \|_{1/2}} }\höger\},$

var

$\|\beta \|_{1/2}=\left(\summa _{j=1}^{p} {\sqrt {|\beta _{j}|}}\right)^{2}$

Det hävdas att bråkkvasinormerna $\ell ^{p}$ ( $0<p<1$ ) ger mer meningsfulla resultat i dataanalys både teoretiskt och empiriskt. Icke-konvexiteten hos dessa kvasinormer komplicerar optimeringsproblemet. För att lösa detta problem utvecklas och implementeras en förväntningsminimeringsprocedur för minimering av funktion

$\min _{\beta \in \mathbb {R} ^{p }}\left\{{\frac {1}{N}}\left\|yX\beta \right\|_{2}^{2}+\lambda \sum _{j=1}^{p} \vartheta (\beta _{j}^{2})\right\},$

där $\vartheta (\gamma )$ är en godtyckligt konkav monotont ökande funktion (till exempel $\vartheta (\gamma )={\sqrt {\gamma }}$ ger lassostraffet och $displaystyle \vartheta (\gamma )=\gamma ^{1/4}}$$}}$ ℓ $\displaystyle \ell ^{$ straff).

Den effektiva algoritmen för minimering är baserad på bitvis kvadratisk approximation av subquadratic growth (PQSQ).

Adaptivt lasso

Det adaptiva lassot introducerades av Zou 2006 för linjär regression och av Zhang och Lu 2007 för proportionell riskregression.

Tidigare lasso

Det tidigare lassot introducerades för generaliserade linjära modeller av Jiang et al. under 2016 för att införliva förhandsinformation, såsom vikten av vissa kovariater. I föregående lasso sammanfattas sådan information till pseudosvar (kallade tidigare svar) ${\hat {y}}^{\mathrm {p} }$ och sedan läggs en ytterligare kriteriumfunktion till det vanliga målet fungera med en lassostraff. Utan förlust av generalitet, i linjär regression, kan den nya objektiva funktionen skrivas som

$\min _{\beta mathbb {R} ^{p}}\left\{{\frac {1}{N}}\left\|yX\beta \right\|_{2}^{2}+{\frac {1}{ N}}\eta \left\|{\hat {y}}^{\mathrm {p} }-X\beta \right\|_{2}^{2}+\lambda \|\beta \|_ {1}\right\},$

vilket motsvarar

$\min _{\beta \in \mathbb {R} ^{p}}\ vänster\{{\frac {1}{N}}\left\|{\tilde {y}}-X\beta \right\|_{2}^{2}+{\frac {\lambda }{1 +\eta }}\|\beta \|_{1}\right\},$

den vanliga lasso objektivfunktionen där svaren $y$ ersätts av ett viktat medelvärde av de observerade svaren och de tidigare svaren ${\displaystyle {\ tilde {y}}=(y+\eta {\hat {y}}^{\mathrm {p} })/(1+\eta )} (kallas de justerade$ svarsvärdena av tidigare information).

kallas parametern ${\displaystyle \eta } en balanseringsparameter, genom att den balanserar den relativa betydelsen av data och tidigare information.$ I extremfallet $\eta =0$ reduceras föregående lasso till lasso. Om $\eta =\infty$ , kommer tidigare lasso enbart att förlita sig på tidigare information för att passa modellen. Dessutom har balanseringsparametern $\eta$ en annan tilltalande tolkning: den styr variansen av $\beta$ i dess tidigare fördelning från en Bayesiansk synvinkel.

Prior lasso är effektivare vid parameteruppskattning och förutsägelse (med ett mindre uppskattningsfel och förutsägningsfel) när förhandsinformationen är av hög kvalitet, och är robust mot förhandsinformation av låg kvalitet med ett bra val av balanseringsparametern η { $displaystyle \eta }$ .

Datorlassolösningar

Huvudartikel: Proximala gradientmetoder för lärande § Lasso-regularisering

Förlustfunktionen hos lassot är inte differentierbar, men en mängd olika tekniker från konvex analys och optimeringsteori har utvecklats för att beräkna lassots lösningsväg. Dessa inkluderar koordinatnedstigning, subgradientmetoder, minsta vinkelregression (LARS) och proximala gradientmetoder. Subgradientmetoder är den naturliga generaliseringen av traditionella metoder som gradient descent och stokastisk gradient descent till det fall där den objektiva funktionen inte är differentierbar på alla punkter. LARS är en metod som är nära knuten till lassomodeller, och i många fall tillåter dem att passa effektivt, även om den kanske inte fungerar bra under alla omständigheter. LARS genererar kompletta lösningsvägar. Proximala metoder har blivit populära på grund av sin flexibilitet och prestanda och är ett område för aktiv forskning. Valet av metod kommer att bero på den specifika lassovarianten, data och tillgängliga resurser. Men proximala metoder fungerar i allmänhet bra.

Val av regulariseringsparameter

Att välja regulariseringsparametern ( $\lambda$ ) är en grundläggande del av lasso. Ett bra värde är väsentligt för prestanda hos lassot eftersom det styr styrkan av krympning och variabelt urval, vilket med måtta kan förbättra både prediktionsnoggrannheten och tolkningsbarheten. Men om regulariseringen blir för stark kan viktiga variabler utelämnas och koefficienter kan krympas överdrivet, vilket kan skada både prediktiv kapacitet och inferens. Korsvalidering används ofta för att hitta regulariseringsparametern.

Informationskriterier som det Bayesianska informationskriteriet (BIC) och Akaike informationskriteriet (AIC) kan vara att föredra framför korsvalidering, eftersom de är snabbare att beräkna och deras prestanda är mindre flyktiga i små urval. Ett informationskriterium väljer skattarens regulariseringsparameter genom att maximera en modells noggrannhet i urvalet samtidigt som dess effektiva antal parametrar/frihetsgrader straffas. Zou et al. föreslagit att mäta de effektiva frihetsgraderna genom att räkna antalet parametrar som avviker från noll. Tillvägagångssättet för frihetsgrader ansågs vara felaktigt av Kaufman och Rosset och Janson et al., eftersom en modells frihetsgrader kan öka även när den straffas hårdare av regulariseringsparametern. Som ett alternativ kan det relativa enkelhetsmåttet som definierats ovan användas för att räkna det effektiva antalet parametrar. För lassot ges detta mått av

${\hat {\mathcal {P}}}=\sum _{i=1}^{p}{\frac {|\beta _{i}-\beta _{0,i}|}{ {\frac {1}{p}}\summa _{l}|b_{OLS,l}-\beta _{0,l}|}}$ ,

som monotont ökar från noll till $p$ när regulariseringsparametern minskar från $\infty$ till noll.

Utvalda applikationer

LASSO har använts inom ekonomi och finans, och visade sig förbättra förutsägelser och välja ibland försummade variabler, till exempel i litteratur om företagskonkurser eller förutsägelser av företag med hög tillväxt.

Se även

• Minsta absoluta avvikelser
• Modellval
• Icke-parametrisk regression
• Tikhonov regularisering