Fission barriär

En inducerad fissionsreaktion . En kärna blir exciterad av någon kärnprocess och delas sedan upp i lättare element ( klyvningsprodukter) . Detta frigör en liten mängd neutroner och prompter gammastrålning , följt av beta-sönderfallet av de lättare kärnorna med ytterligare gammastrålning som frigörs.

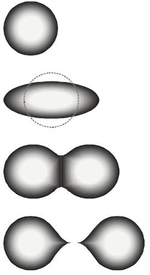
Inom kärnfysik och kärnkemi är fissionsbarriären den aktiveringsenergi som krävs för att en kärna i en atom ska genomgå klyvning . Denna barriär kan också definieras som den minsta mängd energi som krävs för att deformera kärnan till den punkt där den är oåterkalleligen förpliktad till fissionsprocessen. Energin för att övervinna denna barriär kan komma från antingen neutronbombardement av kärnan, där den extra energin från neutronen för kärnan till ett exciterat tillstånd och genomgår deformation, eller genom spontan fission , där kärnan redan är i ett exciterat och deformerat tillstånd .

Det är viktigt att notera att ansträngningar att förstå fissionsprocesser fortfarande pågår och har varit ett mycket svårt problem att lösa sedan fission först upptäcktes av Lise Meitner , Otto Hahn och Fritz Strassmann 1938. Även om kärnfysiker förstår många aspekter av fissionsprocessen, finns det för närvarande ingen omfattande teoretisk ram som ger en tillfredsställande redogörelse för de grundläggande observationerna.

Scission

Klyvningsprocessen kan förstås när en kärna med viss jämviktsdeformation absorberar energi (genom neutroninfångning, till exempel), blir exciterad och deformeras till en konfiguration som kallas "övergångstillstånd" eller "sadelpunkt"-konfiguration. När kärnan deformeras minskar den nukleära Coulomb-energin medan den nukleära ytenergin ökar. Vid sadelpunkten är förändringshastigheten för Coulomb-energin lika med förändringshastigheten för den nukleära ytenergin. Bildandet och det slutliga sönderfallet av denna övergångstillståndskärna är det hastighetsbestämmande steget i fissionsprocessen och motsvarar passagen över en aktiveringsenergibarriär till fissionsreaktionen. När detta inträffar försvinner halsen mellan de begynnande fragmenten och kärnan delar sig i två fragment. Den punkt vid vilken detta inträffar kallas "skärningspunkten".

Flytande droppmodell

Från beskrivningen av början av klyvningsprocessen till "klyvningspunkten" är det uppenbart att förändringen av kärnans form är förknippad med en förändring av energi av något slag. I själva verket är det förändringen av två typer av energier: (1) den makroskopiska energin relaterad till kärnkraftens bulkegenskaper som ges av vätskedroppemodellen och (2) den kvantmekaniska energin som är associerad med att fylla skalmodellens orbitaler. För kärnkraftens bulkegenskaper med små förvrängningar, ytan, $E_{s}$ och Coulomb, $E_{c}$ , ges energierna av:

$E_{s}=E_{s}^{0}\left(1+{\frac {2}{5}}\alpha _{2 }^{2}\right)$

$E_{c}=E_{c}^{0}\left(1-{\frac {1} {5}}\alpha _{2}^{2}\right)$

där $E_{s}^{0}$ och $E_{c}^{0}$ är yt- och Coulomb-energierna för de oförvrängda sfäriska dropparna respektive, och $\alpha _{2}$ är fyrpolig distorsionsparameter. När förändringarna i Coulomb- och ytenergierna ( $\Delta E_{c}=E_{c}^{0}-E_{c}$ , $\Delta E_{s}=E_{s}^{0}-E_{s}$ ) är lika, blir kärnan instabil med avseende på fission. Vid den punkten blir förhållandet mellan den oförvrängda ytan och Coulomb-energierna:

$x={\frac {E_{c}^{0}}{2E_{s}^{0}}}$

där $x$ kallas klyvbarhetsparametern. Om $x>1$ minskar vätskedroppsenergin med ökande ${\displaystyle \alpha _{2}} ,$ vilket leder till fission. Om $x<1$ så minskar vätskedroppsenergin med minskande $\alpha _{2}$ , vilket leder till sfäriska former av kärnan.

Coulomb- och ytenergierna för en enhetligt laddad sfär kan approximeras med följande uttryck:

$E_{c}^{0}={\frac {3}{5}}{\frac {Z ^{2}e^{2}}{R_{0}A^{1/3}}}=a_{c}{\frac {Z^{2}}{A^{1/3}}}$

$E_{s}^{0}=4\pi R_{0}^{2}SA^{2/3}= a_{s}A^{2/3}$

där $Z$ är kärnans atomnummer , $A$ är massnumret för kärnan, $e$ är laddningen för en elektron, $R_{0}$ är radien för den oförvrängda sfäriska kärnan, $S$ är ytspänningen per ytenhet av kärnan, $a_{c}=3e^{2}/ 5R_{0}$ och $a_{s}=4\pi R_{0}^{2}S$ . Ekvationen för klyvbarhetsparametern blir då:

$x=\left({\frac {a_{c} }{2a_{s}}}\right)\left({\frac {Z^{2}}{A}}\right)=\left({\frac {Z^{2}}{A}}\ höger)/\left({\frac {Z^{2}}{A}}\right)_{kritisk}$

där förhållandet mellan konstanten $\left(a_{c}/2a_{s}\right)^{-1}$ hänvisas till som $\left(Z^{2}/A\right)_{kritisk}$ . Klyvbarheten för en given kärna kan sedan kategoriseras i förhållande till $\left(Z^{2}/A\right)$ . Som ett exempel har plutonium-239 ett ${\displaystyle \left(Z^{2}/A\right)}-$ värde på 36,97, medan mindre klyvbara kärnor som vismut-209 har ett $\left(Z^{2}/A\right)$ värde på 32,96.

För alla stabila kärnor måste $x$ vara mindre än 1. I så fall kommer den totala deformationsenergin för kärnor som genomgår fission att öka med en mängd ${\displaystyle (1/5)\alpha _{2}^{2}(2E_{s}^{0}-E_{c}^{0})} ,$ när kärnan deformeras mot fission. Denna ökning av potentiell energi kan ses som aktiveringsenergibarriären för fissionsreaktionen. Moderna beräkningar av den potentiella deformationsenergin för vätskedroppsmodellen involverar dock många deformationskoordinater bortsett från $\alpha _{2}$ och representerar stora beräkningsuppgifter.

Skalkorrigeringar

För att få mer rimliga värden för kärnmassorna i vätskedroppemodellen är det nödvändigt att ta med skaleffekter. Den sovjetiske fysikern Vilen Strutinsky föreslog en sådan metod med hjälp av "skalkorrigering" och korrigeringar för kärnkraftsparning till vätskedroppemodellen. I denna metod tas kärnans totala energi som summan av vätskedroppsmodellens energi, $E_{LDM}$ , skalet, $\delta S$ och parning , $\delta P$ , korrigeringar av denna energi som:

$E=E_{LDM}+\summa _{p,n}(\delta S+\delta P)$

Skalkorrigeringarna, precis som vätskedroppsenergin, är funktioner av kärndeformationen. Skalkorrigeringarna tenderar att sänka grundtillståndsmassorna av sfäriska kärnor med magiska eller nästan magiska antal neutroner och protoner . De tenderar också att sänka grundtillståndsmassan hos kärnor i mitten av skalet vid någon ändlig deformation och därmed förklara aktinidernas deformerade natur . Utan dessa skaleffekter kunde de tyngsta kärnorna inte observeras, eftersom de skulle sönderfalla genom spontan fission på en tidsskala som är mycket kortare än vi kan observera.

Denna kombination av makroskopiska vätskedroppar och mikroskopiska skaleffekter förutspår att för kärnor i U - Pu -regionen kommer en dubbelpuckel fissionsbarriär med lika barriärhöjder och ett djupt sekundärt minimum att inträffa. För tyngre kärnor, som californium , förutsägs den första barriären vara mycket större än den andra barriären och passage över den första barriären är hastighetsbestämmande. I allmänhet finns det gott om experimentella och teoretiska bevis för att den lägsta energivägen i fissionsprocessen motsvarar att kärnan, initialt i en axiellt symmetrisk och mass (reflektions) symmetrisk form passerar över det första maximum i fissionsbarriären med en axiellt asymmetrisk men masssymmetrisk form och sedan att passera över det andra maximum i barriären med en axiellt symmetrisk men mass (reflektion) asymmetrisk form. På grund av den komplicerade flerdimensionella karaktären hos fissionsprocessen finns det inga enkla formler för fissionsbarriärens höjder. Det finns dock omfattande tabeller över experimentella karakteriseringar av klyvningsbarriärens höjder för olika kärnor.

Se även

• Kall fission
• Kärnfusion