Fanno flow
Fannoflöde är det adiabatiska flödet genom en kanal med konstant area där effekten av friktion beaktas. Kompressibilitetseffekter kommer ofta i beaktande, även om Fanno-flödesmodellen säkert också gäller för inkompressibelt flöde . För denna modell förblir kanalarean konstant, flödet antas vara jämnt och endimensionellt och ingen massa tillförs i kanalen. Fanno-flödesmodellen anses vara en irreversibel process på grund av viskösa effekter. Den viskösa friktionen gör att flödesegenskaperna förändras längs kanalen. Friktionseffekten är modellerad som en skjuvspänning vid väggen som verkar på vätskan med enhetliga egenskaper över alla tvärsnitt av kanalen.
För ett flöde med ett uppströms Mach-tal större än 1,0 i en tillräckligt lång kanal uppstår en retardation och flödet kan täppas till . Å andra sidan, för ett flöde med ett uppströms Mach-tal mindre än 1,0, uppstår acceleration och flödet kan täppas till i en tillräckligt lång kanal. Det kan visas att för flöde av kalorimässigt perfekt gas inträffar den maximala entropin vid M = 1,0. Fanno flow är uppkallat efter Gino Girolamo Fanno .
Teori
Fanno-flödesmodellen börjar med en differentialekvation som relaterar förändringen i Mach-tal med avseende på längden på kanalen, dM/dx . Andra termer i differentialekvationen är värmekapacitetsförhållandet , γ , fläktfriktionsfaktorn , f , och den hydrauliska diametern , Dh :
Om vi antar att fläktfriktionsfaktorn är en konstant längs kanalväggen, kan differentialekvationen lösas enkelt. Man måste dock komma ihåg att värdet på Fanning-friktionsfaktorn kan vara svårt att bestämma för överljuds- och speciellt hypersoniska flödeshastigheter. Den resulterande relationen visas nedan där L* är den erforderliga kanallängden för att strypa flödet förutsatt att uppströms Mach-talet är överljud. Den vänstra sidan kallas ofta Fanno-parametern.
Lika viktigt för Fanno-flödesmodellen är det dimensionslösa förhållandet mellan förändringen i entropi över värmekapaciteten vid konstant tryck, c p .
Ovanstående ekvation kan skrivas om i termer av ett statiskt till stagnationstemperaturförhållande, vilket, för en kalorimässigt perfekt gas, är lika med det dimensionslösa entalpiförhållandet, H :
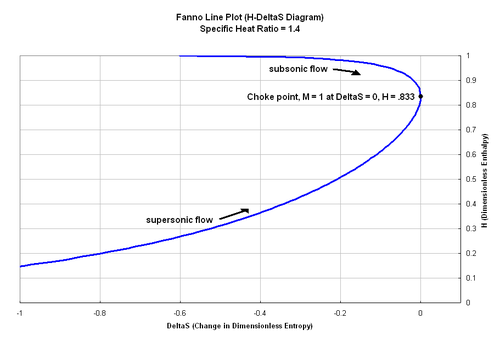
Ekvationen ovan kan användas för att plotta Fanno-linjen, som representerar ett läge av tillstånd för givna Fanno-flödesförhållanden på ett H - ΔS -diagram. I diagrammet når Fanno-linjen maximal entropi vid H = 0,833 och flödet stryps. Enligt termodynamikens andra lag måste entropin alltid öka för Fanno-flödet. Detta innebär att ett subsoniskt flöde som kommer in i en kanal med friktion kommer att öka sitt Mach-tal tills flödet stryps. Omvänt kommer Mach-talet för ett överljudsflöde att minska tills flödet stryps. Varje punkt på Fanno-linjen motsvarar ett annat Mach-nummer, och rörelsen till strypt flöde visas i diagrammet.
Fanno-linjen definierar de möjliga tillstånden för en gas när massflödeshastigheten och den totala entalpin hålls konstant, men momentumet varierar. Varje punkt på Fanno-linjen kommer att ha ett annat momentumvärde, och förändringen i momentum kan tillskrivas effekterna av friktion.
Ytterligare Fanno-flödesrelationer
Som tidigare nämnts hålls arean och massflödet i kanalen konstant för Fannoflöde. Dessutom stagnationstemperaturen konstant. Dessa relationer visas nedan med symbolen * som representerar platsen för halsen där kvävning kan inträffa. En stagnationsegenskap innehåller en 0-subskript.
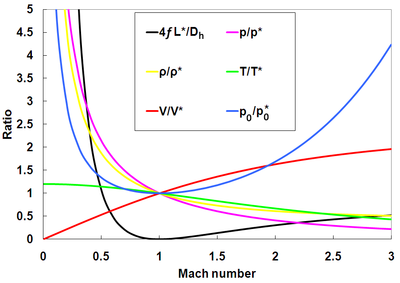
Differentialekvationer kan också utvecklas och lösas för att beskriva Fanno-flödesegenskapsförhållanden med avseende på värdena vid kvävningsplatsen. Förhållandena för tryck, densitet, temperatur, hastighet och stagnationstryck visas nedan. De representeras grafiskt tillsammans med Fanno-parametern.
Ansökningar


Fanno-flödesmodellen används ofta vid design och analys av munstycken. I ett munstycke modelleras det konvergerande eller divergerande området med isentropiskt flöde, medan sektionen med konstant area efteråt modelleras med Fannoflöde. För givna uppströmsförhållanden vid punkt 1, såsom visas i figurerna 3 och 4, kan beräkningar göras för att bestämma munstyckets utgångs Mach-tal och platsen för en normal stöt i kanalen med konstant area. Punkt 2 markerar munstyckshalsen, där M = 1 om flödet är strypt. Punkt 3 markerar änden av munstycket där flödet övergår från isentropiskt till Fanno. Med ett tillräckligt högt initialtryck kan överljudsflödet upprätthållas genom kanalen med konstant area, liknande den önskade prestandan hos en överljudsvindtunnel av avblåsningstyp . Dessa figurer visar dock stötvågen innan den har rört sig helt genom kanalen. Om en stötvåg förekommer övergår flödet från den överljudsdelen av Fanno-linjen till den subsoniska delen innan den fortsätter mot M = 1. Rörelsen i figur 4 är alltid från vänster till höger för att uppfylla den andra lagen av termodynamik.
Fanno-flödesmodellen används också flitigt med Rayleigh-flödesmodellen . Dessa två modeller skär varandra i punkter på entalpi-entropi- och Mach-tal-entropidiagrammen, vilket är meningsfullt för många tillämpningar. Entropivärdena för varje modell är dock inte lika vid ljudtillståndet. Förändringen i entropi är 0 vid M = 1 för varje modell, men föregående påstående betyder att förändringen i entropi från samma godtyckliga punkt till ljudpunkten är annorlunda för Fanno- och Rayleigh-flödesmodellerna. Om initiala värden för si och Mi definieras, kan en ny ekvation för dimensionslös entropi kontra Mach-tal definieras för varje modell . Dessa ekvationer visas nedan för Fanno- respektive Rayleigh-flöde.
Figur 5 visar Fanno- och Rayleigh-linjerna som skär varandra för initiala förhållanden av s i = 0 och M i = 3. Skärningspunkterna beräknas genom att likställa de nya dimensionslösa entropiekvationerna med varandra, vilket resulterar i relationen nedan.
Skärningspunkterna inträffar vid det givna initiala Mach-talet och dess postnormala stötvärde . För figur 5 är dessa värden M = 3 och 0,4752, vilket kan hittas i de normala stöttabellerna som listas i de flesta läroböcker för komprimerbart flöde. Ett givet flöde med konstant kanalarea kan växla mellan Fanno- och Rayleigh-modellerna vid dessa punkter.
Se även
- Rayleigh flöde
- Isentropisk process
- Isotermiskt flöde
- Gasdynamik
- Kompressibelt flöde
- Kvävt flöde
- Entalpi
- Entropi
- Isentropiskt munstycksflöde
externa länkar
- Purdue University Adiabatic och Isothermal Fanno flödeskalkylatorer
- University of Kentucky Fanno flödeswebbkalkylator
- Maurice W. Downey, Gino Fanno

![\ \frac{4fL^*}{D_h} = \left(\frac{1 - M^2}{\gamma M^2}\right) + \left(\frac{\gamma + 1}{2\gamma}\right)\ln\left[\frac{M^2}{\left(\frac{2}{\gamma + 1}\right)\left(1 + \frac{\gamma - 1}{2}M^2\right)}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/97d3400a03fe159951756769bd5df8f2607a20b8)
![\ \Delta S = \frac{\Delta s}{c_p} = \ln\left[M^\frac{\gamma - 1}{\gamma}\left(\left[\frac{2}{\gamma + 1}\right]\left[1 + \frac{\gamma - 1}{2}M^2\right]\right)^\frac{-(\gamma + 1)}{2\gamma}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/c679a2d173adae85d4f6436444b15048ec999f8b)

![\ \Delta S = \frac{\Delta s}{c_p} = \ln\left[\left(\frac{1}{H} - 1\right)^\frac{\gamma - 1}{2\gamma}\left(\frac{2}{\gamma - 1}\right)^\frac{\gamma - 1}{2\gamma}\left(\frac{\gamma + 1}{2}\right)^\frac{\gamma + 1}{2\gamma}\left(H\right)^\frac{\gamma + 1}{2\gamma}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/0dab1f349013744ebcf2e6ceefa006a98f85ee8b)

![\begin{align}
\frac{p}{p^*} &= \frac{1}{M}\frac{1}{\sqrt{\left(\frac{2}{\gamma + 1}\right)\left(1 + \frac{\gamma - 1}{2}M^2\right)}} \\
\frac{\rho}{\rho^*} &= \frac{1}{M}\sqrt{\left(\frac{2}{\gamma + 1}\right)\left(1 + \frac{\gamma - 1}{2}M^2\right)} \\
\frac{T}{T^*} &= \frac{1}{\left(\frac{2}{\gamma + 1}\right)\left(1 + \frac{\gamma - 1}{2}M^2\right)} \\
\frac{V}{V^*} &= M\frac{1}{\sqrt{\left(\frac{2}{\gamma + 1}\right)\left(1 + \frac{\gamma - 1}{2}M^2\right)}} \\
\frac{p_0}{p_0^*} &= \frac{1}{M}\left[\left(\frac{2}{\gamma + 1}\right)\left(1 + \frac{\gamma - 1}{2}M^2\right)\right]^\frac{\gamma + 1}{2\left(\gamma - 1\right)}
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/caf30572891bf439a34e222c067d4f14b8e76ab0)

![\begin{align}
\Delta S_F &= \frac{s - s_i}{c_p} = \ln\left[\left(\frac{M}{M_i}\right)^\frac{\gamma - 1}{\gamma}\left(\frac{1 + \frac{\gamma - 1}{2}M_i^2}{1 + \frac{\gamma - 1}{2}M^2}\right)^\frac{\gamma + 1}{2\gamma}\right] \\
\Delta S_R &= \frac{s - s_i}{c_p} = \ln\left[\left(\frac{M}{M_i}\right)^2\left(\frac{1 + \gamma M_i^2}{1 + \gamma M^2}\right)^\frac{\gamma + 1}{\gamma}\right]
\end{align}](https://wikimedia.org/api/rest_v1/media/math/render/svg/31b696ced22bb1df158e11d46ce5b9f5a19b64b5)
![\ \left(1 + \frac{\gamma - 1}{2}M_i^2\right)\left[\frac{M_i^2}{\left(1 + \gamma M_i^2\right)^2}\right] = \left(1 + \frac{\gamma - 1}{2}M^2\right)\left[\frac{M^2}{\left(1 + \gamma M^2\right)^2}\right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/1031340758891c29e5707e01def7e1c5983b548d)