Excentrisk anomali

Inom orbitalmekanik är den excentriska anomali en vinkelparameter som definierar positionen för en kropp som rör sig längs en elliptisk Keplerbana . Den excentriska anomalien är en av tre vinkelparametrar ("anomalier") som definierar en position längs en omloppsbana, de andra två är den sanna anomalien och den genomsnittliga anomalien .

Grafisk representation

Den excentriska anomin för punkt P är vinkeln E . Mitten av ellipsen är punkt O, och fokus är punkt F .

Betrakta ellipsen med ekvation ges av:

${\frac {x^{2}}{a^{2}}}+{\frac {y^{2}}{b^{2} }}=1,$

där a är halvstoraxeln och b är halvmollaxeln .

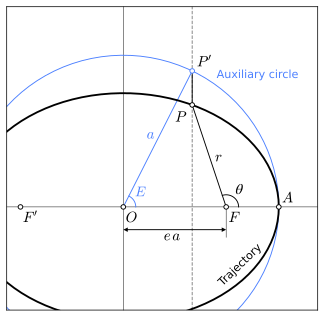
För en punkt på ellipsen, P = P ( x , y ), som representerar positionen för en kretsande kropp i en elliptisk bana, är den excentriska anomali vinkeln E i figuren. Den excentriska anomali E är en av vinklarna i en rätvinklig triangel med en vertex i mitten av ellipsen, dess intilliggande sida ligger på huvudaxeln, har hypotenusa a (lika med ellipsens halvstora axel) och motsatt sida (vinkelrät mot huvudaxeln och vidrör punkten P′ på hjälpcirkeln med radien a ) som passerar genom punkten P . Den excentriska anomin mäts i samma riktning som den sanna anomali, visad i figuren som $\theta$ . Den excentriska anomali E i termer av dessa koordinater ges av:

$\cos E={\frac {x}{a}},$

och

$\sin E={\frac {y}{b}}$

Den andra ekvationen upprättas med hjälp av sambandet

$\left({\frac {y}{b}}\right)^{2}=1-\cos ^{2}E =\sin ^{2}E$ ,

vilket innebär att sin E = ± y / b . Ekvationen sin E = − y / b kan omedelbart uteslutas eftersom den korsar ellipsen i fel riktning. Det kan också noteras att den andra ekvationen kan ses som att den kommer från en liknande triangel där dess motsatta sida har samma längd y som avståndet från P till huvudaxeln , och dess hypotenusa b är lika med halvmollaxeln i ellips.

Formler

Radie och excentrisk anomali

Excentriciteten e definieras som :

$e={\sqrt {1-\left({\frac {b}{a}}\right)^{2}}}\ .$

Från Pythagoras sats tillämpad på triangeln med r (ett avstånd FP ) som hypotenusa:

${\begin{aligned}r^{2 }&=b^{2}\sin ^{2}E+(ae-a\cos E)^{2}\\&=a^{2}\left(1-e^{2}\right)\ left(1-\cos ^{2}E\right)+a^{2}\left(e^{2}-2e\cos E+\cos ^{2}E\right)\\&=a^{ 2}-2a^{2}e\cos E+a^{2}e^{2}\cos ^{2}E\\&=a^{2}\left(1-e\cos E\right )^{2}\\\end{aligned}}$

Således är radien (avståndet från fokus till punkt P ) relaterad till den excentriska anomalien med formeln

$r=a\left(1-e\cos {E}\right)\ .$

Med detta resultat kan den excentriska anomalien bestämmas från den sanna anomalien som visas härnäst.

Från den sanna anomalien

Den sanna anomalien är vinkeln märkt $\theta$ i figuren, placerad vid ellipsens fokus. Det representeras ibland av f eller v . Den sanna anomalien och den excentriska anomalien är relaterade enligt följande.

Med formeln för r ovan hittas sinus och cosinus för E i termer av f :

${\begin{aligned}\cos E&={\frac {\,x\,}{a}}={\frac {\,ae+r\cos f\,}{a}}=e+( 1-e\cos E)\cos f\\\Högerpil \cos E&={\frac {\,e+\cos f\,}{1+e\cos f}}\\\sin E&={\sqrt { \,1-\cos ^{2}E\;}}={\frac {\,{\sqrt {\,1-e^{2}\;}}\,\sin f\,}{1+ e\cos f}}~.\end{aligned}}$

Därav,

$\tan E={\frac {\,\sin E\,}{\cos E}}={\frac {\,{\sqrt {\,1-e^{2}\;}}\ ,\sin f\,}{e+\cos f}}~.$

Vinkel E är därför den intilliggande vinkeln för en rätvinklig triangel med hypotenusan $\;1+e\cos f\;,$ intilliggande sida $\;e+\ cos f\;,$ och motsatt sida $\;{\sqrt {\,1-e^{2}\;}}\,\sin f\;.$

Också,

$\tan {\frac {\,f\,}{2}}={\sqrt {{\frac {\,1+e\, }{1-e}}\,}}\,\tan {\frac {\,E\,}{2}}$

  Genom att ersätta cos E som hittats ovan i uttrycket för r , det radiella avståndet från brännpunkten till punkten P , kan även hittas i termer av den sanna anomalien:

$r={\frac {a\left(\,1-e^{2}\,\right) }{\,1+e\cos f\,}}={\frac {p}{\,1+e\cos f\,}}\,$

var

$\,p\equiv a\left(\,1-e^{2}\,\right)$

kallas "the semi-latus rectum" i klassisk geometri.

Från den genomsnittliga anomalien

Den excentriska anomali E är relaterad till medelanomali M av Keplers ekvation :

$M=Ee\sin E$

Denna ekvation har ingen lösning i sluten form för E givet M . Det löses vanligtvis med numeriska metoder , t.ex. Newton-Raphson-metoden . Det kan uttryckas i en Fourier-serie som

$E=M+2\summa _{n=1}^{\infty }{\frac {J_{ n}(ne)}{n}}\sin(nM)$

där $J_{n}(x)$ är Bessel-funktionen av det första slaget.

Se även

• Excentricitetsvektor
• Orbital excentricitet

Källor

• Murray, Carl D.; & Dermott, Stanley F. (1999); Solar System Dynamics , Cambridge University Press, Cambridge, GB
• Plummer, Henry CK (1960); An Introductory Treatise on Dynamical Astronomy , Dover Publications, New York, NY (Reprint av 1918 Cambridge University Press-utgåvan)