Banfasning

Fasvinkel

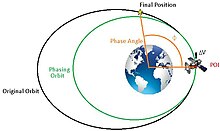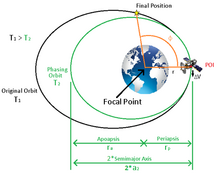
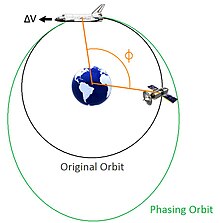
Inom astrodynamik är omloppsfasning justeringen av rymdfarkostens tidsposition längs dess omloppsbana, vanligtvis beskriven som att justera den kretsande rymdfarkostens verkliga anomali. Orbital fasning används främst i scenarier där en rymdfarkost i en given bana måste flyttas till en annan plats inom samma bana. Förändringen i position inom omloppsbanan definieras vanligtvis som fasvinkeln, ϕ, och är förändringen i sann anomali som krävs mellan rymdfarkostens nuvarande position till slutpositionen.

Fasvinkeln kan konverteras i termer av tid med Keplers ekvation:

$t={\frac {T_{1}}{2\pi }}(E-e_{1}\sin E)$

$E=2\arctan({\sqrt {\frac {1-e_{1}}{1+e_{1}}}}\ tan {\frac {\phi }{2}})$

var

t definieras som tiden som förflutit för att täcka fasvinkeln i den ursprungliga omloppsbanan

T ₁ definieras som perioden för den ursprungliga omloppsbanan

E definieras som förändring av excentrisk anomali mellan rymdskepp och slutposition

e ₁ definieras som orbital excentricitet för ursprunglig omloppsbana

Φ definieras som förändring i sann anomali mellan rymdskepp och slutposition

Fasomlopp
Om rymdfarkosten befinner sig bakom den slutliga positionen på samma omloppsbana måste rymdfarkosten sakta ner för att gå in i en mindre, snabbare fasbana för att komma ikapp till slutpositionen.

Denna tid som härleds från fasvinkeln är den tid som krävs för att rymdfarkosten måste vinna eller förlora för att vara placerad vid den slutliga positionen i omloppsbanan. För att vinna eller förlora denna tid måste rymdfarkosten utsättas för en enkel tvåimpuls Hohmann-överföring som tar rymdfarkosten bort från och sedan tillbaka till sin ursprungliga omloppsbana. Den första impulsen för att ändra rymdfarkostens omloppsbana utförs vid en specifik punkt i den ursprungliga omloppsbanan (pulspunkt, POI), vanligtvis utförd i den ursprungliga omloppsbanans periapsis eller apoapsis . Impulsen skapar en ny omloppsbana som kallas "fasande omloppsbana" och är större eller mindre än den ursprungliga omloppsbanan, vilket resulterar i en annan tidsperiod än den ursprungliga omloppsbanan. Skillnaden i periodtid mellan den ursprungliga och fasningsbanan kommer att vara lika med tiden omvandlad från fasvinkeln. När en period av fasomloppsbanan är klar kommer rymdfarkosten att återvända till POI och rymdfarkosten kommer återigen att utsättas för en andra impuls, lika med och motsatt den första impulsen, för att återföra den till den ursprungliga omloppsbanan. När det är färdigt kommer rymdfarkosten att vara i den slutliga positionen i den ursprungliga omloppsbanan.

För att hitta några av fasningsorbitalparametrarna måste man först hitta den erforderliga tidsperioden för fasningsbanan med hjälp av följande ekvation.

$T_{2}=T_{1}-t$

var

T ₁ definieras som perioden för den ursprungliga omloppsbanan

T ₂ är definierad som perioden för fasningsomloppsbanan

t definieras som tiden som förflutit för att täcka fasvinkeln i den ursprungliga omloppsbanan

När väl fasningsomloppsperioden har bestämts, kan fasomloppsbanans semimajoraxel härledas från periodformeln:

$a_{2}=({\frac {{\sqrt {\mu }}T_{2}}{2\pi }})^{\frac { 2}{3}}$

var

a ₂ definieras som fasningsbanas halvhuvudaxel

T ₂ definieras som fasningsbanan

μ definieras som standardgravitationsparameter

Från halvhuvudaxeln kan fasbanan apogeum och perigeum beräknas:

$2a_{2}=r_{a}+r_{p}$

var

a ₂ definieras som fasningsbanas halvhuvudaxel

r _a definieras som fasningsbanas apogee

r _p definieras som fasningsbanas perigeum

Slutligen kan den fasande omloppsbanans rörelsemängd hittas från ekvationen:

$h_{2}={\sqrt {2\mu }}{\sqrt {\frac {r_{a}r_{p}}{r_{ a}+r_{p}}}}$

var

h ₂ definieras som vinkelmomentum för fasningsomloppsbana

r _a definieras som höjdpunkt för fasningsbana

r _p definieras som perigeum av fasningsbana

μ definieras som standardgravitationsparameter

För att hitta den impuls som krävs för att ändra rymdfarkosten från dess ursprungliga bana till fasbanan, måste ändringen av rymdfarkostens hastighet, ∆V , vid POI beräknas från vinkelmomentformeln:

$\Delta V=v_{2}-v_{1}={\frac {h_{2}}{r}}-{\frac {h_{1}}{r}}$

var

∆V är förändring i hastighet mellan fasning och ursprungliga banor vid POI

v ₁ definieras som rymdfarkostens hastighet vid POI i ursprunglig omloppsbana

v ₂ definieras som rymdfarkostens hastighet vid POI i fasande omloppsbana r

definieras som radien för rymdskepp från omloppsbanans fokal punkt till POI

h ₁ definieras som rörelsemängd för den ursprungliga omloppsbanan

h ₂ definieras som rörelsemängd för fasningsbana

Samorbital Rendezvous
Om målet (satelliten) befinner sig bakom rymdfarkosten (skytteln) i samma omloppsbana, måste rymdfarkosten öka för att gå in i en större, långsammare fasbana för att tillåta målet att komma ikapp.

Kom ihåg att denna förändring i hastighet, ∆V , bara är den mängd som krävs för att ändra rymdfarkosten från sin ursprungliga bana till fasbanan. En andra förändring i hastighet lika med storleken men motsatt i riktningen av den första måste göras efter att rymdfarkosten färdats en fasomloppsperiod för att återföra rymdfarkosten från fasbanan till den ursprungliga omloppsbanan. Den totala hastighetsändringen som krävs för fasningsmanövern är lika med två gånger ∆V .

Banfasning kan också refereras till som co-orbital rendezvous som ett framgångsrikt närmande till en rymdstation i en dockningsmanöver. Här möts två rymdfarkoster på samma bana men vid olika sanna anomalier genom att antingen en eller båda rymdfarkosterna går in i fasbanor som får dem att återgå till sin ursprungliga bana vid samma sanna anomali samtidigt.

Fasningsmanövrar används också vanligtvis av geosynkrona satelliter, antingen för att utföra stationsmanövrar för att behålla sin omloppsbana över en specifik longitud, eller för att ändra longitud helt och hållet.

Se även

• Orbital manöver
• Hohmann överföringsbana
• Clohessy-Wiltshire ekvationer för sambana analys
• Rymden möte

Allmän

•   Curtis, Howard D (2014). Orbital Mechanics for Engineering Students (tredje upplagan). Butterworth-Heinemann. ISBN 978-0-08-097747-8 .
•   Francis, Hale J (1994). Introduktion till rymdflygning . Prentice-Hall, Inc. ISBN 0-13-481912-8 .
•   Sellers, Jerry Jon; Marion, Jerry B. (2005). Understanding Space An Introduction to Astronautics (tredje upplagan). McGraw-Hill. ISBN 978-0-07-340775-3 .
• Hall, Christopher D.; Collazo-Perez, Victor (november 2003). "Minimum-Time Orbital Phasing Manövrar" . Journal of Guidance, Control, and Dynamics . 26 (6) . Hämtad 2 januari 2023 .

• Fasningsmanöver