Descendentträd (gruppteori)

Inom matematik, särskilt gruppteori , är ett ättlingträd en hierarkisk struktur som visualiserar förälder-ättling-relationer mellan isomorfismklasser av ändliga grupper av primtalsordning $p^{n}$ , för ett fast primtal ${\ displaystyle p}$ och varierande heltalsexponenter $n\geq 0$ . Sådana grupper kallas kortfattat ändliga p-grupper . Topparna av ett avkommande träd är isomorfismklasser av ändliga p -grupper .

Utöver sin ordning $p^{n}$ , har finita p -grupper ytterligare två relaterade invarianter, nilpotensklassen $c$ och coklassen $r=nc$ . Det visade sig att efterkommande träd av ett särskilt slag, de så kallade beskurna samklassträden vars oändligt många hörn delar en gemensam samklass $r$ , avslöjar ett återkommande ändligt mönster. Dessa två avgörande egenskaper av ändlighet och periodicitet medger en karakterisering av alla medlemmar av trädet genom ändligt många parametriserade presentationer . Följaktligen spelar efterkommande träd en grundläggande roll i klassificeringen av ändliga p -grupper. Med hjälp av kärnor och mål av Artin transfer homomorphisms , kan avkommande träd förses med ytterligare struktur.

En viktig fråga är hur det efterkommande trädet ${\mathcal {T}}(R)$ faktiskt kan konstrueras för en tilldelad startgrupp som tas som roten R $\displaystyle R}$ i trädet . Algoritmen för generering av p -grupp är en rekursiv process för att konstruera det efterkommande trädet för en given finit p -grupp som spelar rollen som trädroten. Denna algoritm är implementerad i beräkningsalgebrasystemen GAP och Magma .

Definitioner och terminologi

Enligt MF Newman finns det flera distinkta definitioner av föräldern $\pi (G)$ för en finit p -grupp $G$ . Den vanliga principen är att bilda kvoten $\pi (G)=G/N$ av $G$ av en lämplig normal undergrupp $N\triangleleft G$ som kan vara antingen

P

1. mitten N $N=\zeta _{1}(G)$ av $G$ varav $\pi (G)=G/\zeta _{1}(G)$ kallas den centrala kvoten av $G$ , eller
2. den sista icke-triviala termen $N=\gamma _{c}(G)$ i den nedre centrala serien av $G$ , där $c$ betecknar nilpotensklass för $G$ , eller
3. den sista icke-triviala termen $N=P_{c-1}(G)$ i den nedre exponent- p centralserien av $G$ , där ${\ displaystyle c}$ anger exponent- p -klassen för $G$ , eller
4. den sista icke-triviala termen $N=G^{(d-1)}$ i den härledda serien av $G$ , där $d$ betecknar härledd längd av $G$ .

I varje fall kallas ${\displaystyle G} en$ omedelbar ättling av $\pi (G)$ och en riktad kant av trädet definieras antingen av $G \to \pi (G)$ i den kanoniska projektionens riktning $\pi :G\to \pi (G)$ på kvoten ${ \displaystyle \pi (G)=G/N}$ eller med $\pi (G)\to G$ i motsatt riktning, vilket är mer vanligt för avkomlingar. Den tidigare konventionen antas av CR Leedham-Green och MF Newman, av M. du Sautoy och D. Segal, av CR Leedham-Green och S. McKay och av B. Eick, CR Leedham-Green, MF Newman och EA O 'Brien. Den senare definitionen används av MF Newman, av MF Newman och EA O'Brien, av M. du Sautoy och av B. Eick och CR Leedham-Green.

I det följande väljs riktningen för de kanoniska projektionerna för alla kanter. Då, mer allmänt, är en vertex $R$ en avkomling av en vertex $P$ , och $P$ är en förfader till $R$ , om antingen $R$ är lika med $P$ eller så finns det en sökväg

$(1)\qquad R=Q_{0}\to Q_{1}\to \cdots \to Q_{m -1}\till Q_{m}=P$ , med $m\geq 1$ ,

av riktade kanter från $R$ till $P$ . De hörn som bildar banan sammanfaller med nödvändighet med de itererade föräldrarna $Q_{j}=\pi ^{j}(R)$ av $R$ , med $0\leq j\leq m$ :

${\displaystyle (2)\qquad R=\pi ^{0}( R)\to \pi ^{1}(R)\to \cdots \to \pi ^{m-1}(R)\to \pi ^{m}(R)=P} ,$ med ${ \displaystyle m\geq 1}$ ,

$R/\gamma _{ c+1-j}(R)$ kvoter, kan de också ses som de successiva kvoterna av klass $cj$ av $R$ när nilpotensklassen för $R$ ges av $c\geq m$ :

${\displaystyle (3)\qquad R\simeq R/\gamma _{c+1}(R)\to R/\gamma _{c}(R)\to \cdots \to R/\gamma _{c +2-m}(R)\till R/\gamma _{c+1-m}(R)\simeq P} ,$ med $c\geq m\geq 1$ .

Generellt är det avkomliga trädet ${\mathcal {T}}(G)$ i en vertex $G$ underträdet för alla avkomlingar till $G$ , med början vid roten $G$ . Det maximalt möjliga efterkommande trädet ${\mathcal {T}}(1)$ i trivialgruppen $1$ innehåller alla ändliga p -grupper och är något exceptionellt, eftersom, för alla överordnade definitioner (P1–P4), den triviala gruppen $1$ har oändligt många abelska p -grupper som sina omedelbara ättlingar. De överordnade definitionerna (P2–P3) har fördelen att varje icke-trivial finit p -grupp (av ordningen delbar med $p$ ) bara har ändligt många omedelbara ättlingar.

Prop- grupper och samklassträd

För en god förståelse av propgrupper . samklassträd som en speciell förekomst av avkommande träd är det nödvändigt att sammanfatta några fakta om oändliga topologiska Medlemmarna $\gamma _{j}(S)$ , med $j\geq 1$ , i den nedre centrala serien av en prop- grupp S $\displaystyle S }$ är slutna (och öppna) undergrupper av finita index, och därför är motsvarande kvoter $S/\gamma _{j}(S)$ finita p -grupper. Prop- gruppen S $\displaystyle S}$ sägs vara av samklass $\mathrm {cc} (S)=r$ när gränsen ${\displaystyle r=\lim _{j\to \infty }\,\mathrm {cc} (S/\gamma _{j}(S))} av samklassen för den$ successiva kvoter finns och är ändliga. En oändlig prop - grupp $S$ av coclass $r$ är en p -adic pre- space-grupp , eftersom den har en normal undergrupp ${\displaystyle T} ,$ översättningsgruppen , som är en fri modul över ringen $\mathbb {Z} _{p}$ av p -adiska heltal av unikt bestämd rang ${\displaystyle d} ,$ dimensionen , så att kvoten ${\ displaystyle P=S/T}$ är en ändlig p -grupp, punktgruppen , som verkar på $T$ uniseriellt . Dimensionen ges av

$(4)\qquad d=(p-1)p^{s}$ , med några $0\leq s<r$ .

Ett centralt ändlighetsresultat för oändliga pro- grupper av samklass $r$ tillhandahålls av den så kallade satsen D , som är en av de fem samklasssatser som bevisades 1994 oberoende av A. Shalev och av CR Leedham-Green , och gissade redan 1980 av CR Leedham-Green och MF Newman. Sats D hävdar att det bara finns ändligt många isomorfismklasser av oändliga prop- grupper av samklass $r$ , för alla fixerade primtal $p$ och alla fasta icke-negativa heltal $r$ . Som en konsekvens, om $S$ är en oändlig prop- grupp av samklass $r$ , så finns det ett minimalt heltal $i\geq 1$ så att följande tre villkor är uppfyllda för alla heltal $j\geq i$ .

S

1. $\mathrm {cc} (S/\gamma _{j}(S))=r$ ,
2. $S/\gamma _{j}(S)$ är inte en lägre central kvot av någon oändlig prop- grupp av samklass $r$ som inte är isomorf till ${ \displaystyle S}$ ,
3. $\gamma _{j}/\gamma _{j+1}(S)$ är cyklisk av ordningen $p$ .

Det efterkommande trädet ${\displaystyle {\mathcal {T}}(R)} ,$ med avseende på den överordnade definitionen (P2), av roten $R=S /\gamma _{i}(S)$ med minimal $i$ kallas samklassträdet ${\mathcal {T}}(S)$ av $S$ och dess unika maximala oändliga (omvänd riktade) väg

$(5)\qquad R=S/\gamma _{ i}(S)\leftarrow S/\gamma _{i+1}(S)\leftarrow S/\gamma _{i+2}(S)\leftarrow \cdots$

kallas trädets huvudlinje (eller stam ).

Figur 1: Ett ättlingträd. Grenarna B(2),B(4) har djup 0, och B(5),B(7), resp. B(6),B(8), är isomorfa som träd.

Träddiagram

Ytterligare terminologi, som används i diagram som visualiserar ändliga delar av efterkommande träd, förklaras i figur 1 med hjälp av ett konstgjort abstrakt träd. På den vänstra sidan indikerar en nivå den grundläggande top-down designen för ett efterkommande träd. För betongträd, som de i figur 2, resp. I figur 3 etc. ersätts nivån vanligtvis av en orderskala som ökar från toppen till botten. En vertex är kapabel (eller utdragbar ) om den har minst en omedelbar ättling, annars är den terminal (eller ett löv ). Vertices som delar en gemensam förälder kallas syskon .

Om det efterkommande trädet är ett samklassträd ${\mathcal {T}}(R)$ med rot $R=R_{0}$ och med huvudlinjehörn $(R_{n})_{n\geq 0}$ märkt enligt nivån $n$ , sedan det finita underträdet definierat som skillnadsmängden

$(6)\qquad {\mathcal {B}}(n)={\mathcal {T}}(R_{ n})\setminus {\mathcal {T}}(R_{n+1})$

kallas trädets n: te gren (eller kvist ) eller även grenen ${\mathcal {B}}(R_{n})$ med rot $R_{n}$ , för alla $n\geq 0$ . Djupet på en gren är den maximala längden på de banor som förbinder dess hörn med dess rot . Figur 1 visar ett artificiellt abstrakt samklassträd vars grenar ${\mathcal {B}}(2)$ och ${\mathcal {B}}(4)$ båda har djup $0$ , och grenarna ${\mathcal {B}}(5)\simeq {\mathcal {B}}(7)$ och ${\mathcal {B}}(6)\simeq {\mathcal {B}}(8)$ är parvis isomorfa som grafer. Om alla hörn med djup som är större än ett givet heltal $k\geq 0$ tas bort från grenen ${\mathcal {B}}(n)$ , då får vi djupet- $k$ beskuren gren ${\mathcal {B}}_{k}(n)$ . På motsvarande sätt har djup- $k$ beskuren samklassträd ${\displaystyle {\mathcal {T}}_{k}(R)} ,$ resp. hela samklassträdet ${\mathcal {T}}(R)$ , består av den oändliga sekvensen av dess beskurna grenar $({\mathcal {B }}_{k}(n))_{n\geq 0}$ , resp. grenar ${\displaystyle ({\mathcal {B}}(n))_{n\geq 0}} ,$ sammankopplade av huvudlinjen, vars hörn $R_{n}$ kallas oändligt kapabla .

Virtuell periodicitet

Periodiciteten hos grenar av djupbeskärade samklassträd har bevisats med analytiska metoder som använder zetafunktioner för grupper av M. du Sautoy och med algebraiska tekniker som använder kohomologigrupper av B. Eick och CR Leedham-Green. De förra metoderna medger den kvalitativa insikten om ultimat virtuell periodicitet , de senare metoderna bestämmer den kvantitativa strukturen.

Sats. För varje oändlig prop - grupp $S$ av samklass $r\geq 1$ och dimension $d$ , och för varje givet djup $k\geq 1$ , det finns en effektiv minimal nedre gräns $f(k)\geq 1$ , där periodiciteten av längden $d$ av beskurna grenar av samklassträdet ${\ displaystyle {\mathcal {T}}(S)}$ sätter in, det vill säga det finns grafisomorfismer

$(7)\qquad {\mathcal {B}}_{k}(n+d)\simeq {\mathcal {B}}_ {k}(n)$ för alla $n\geq f(k)$ .

För beviset, klicka på visa på höger sida.

Bevis

Grafens isomorfismer av djup- $k$ beskurna grenar med rötter av tillräckligt stor ordning $n\geq f(k)$ härleds med kohomologiska metoder i sats 6, sid. 277 och sats 9, sid. 278 av Eick och Leedham-Green och den effektiva nedre gränsen $f(k)$ för grenrotsordningarna fastställs i sats 29, sid. 287, i denna artikel.

Dessa centrala resultat kan uttryckas osttensivt: När vi tittar på ett samklassträd genom ett par blinkers och ignorerar ett ändligt antal pre-periodiska grenar i toppen, då kommer vi att se ett upprepat ändligt mönster ( ultimat periodicitet ) . Men om vi tar bredare blinkers kan det pre-periodiska initiala avsnittet bli längre ( virtuell periodicitet).

Toppunkten $P=R_{f(k)}$ kallas den periodiska roten av det beskurna samklassträdet, för ett fast värde på djupet $k$ . Se figur 1.

Multifurkations- och samklassgrafer

Antag att föräldrar till finita p -grupper definieras som sista icke-triviala lägre centrala kvoter (P2). För en p -grupp $G$ av samklassen $\mathrm {cc} (G)=r$ , kan vi urskilja dess (hela) efterkommande träd ${\ displaystyle {\mathcal {T}}(G)}$ och dess samklass - $r$ ättlingträd ${\displaystyle {\mathcal {T}}^{r}(G)} ,$ dvs. underträdet som består av avkomlingar av coclass $r$ endast. Gruppen $G$ kallas coclass-settled om ${\mathcal {T}}(G)={\mathcal {T}}^{r}( G)$ , dvs om det inte finns några ättlingar till $G$ med större samklass än $r$ .

Den nukleära rangordningen $\nu (G)$ för $G$ i teorin för p -gruppsgenereringsalgoritmen av MF Newman och EA O'Brien tillhandahåller följande kriterier.

N

1. $G$ är terminal, och därmed trivialt samklassbestämd, om och endast om $\nu (G)=0$ .
2. Om $\nu (G)=1$ så är $G$ kapabel, men det förblir okänt om $G$ är coclass-settled.
3. Om $\nu (G)=m\geq 2$ , så är $G$ kapabel och definitivt inte samklassbestämd.

I det sista fallet är ett mer exakt påstående möjligt: ​​Om $G$ har samklass $r$ och nukleär rang $\nu (G)=m\geq 2$ , då ger det upphov till en m -faldig multifurkation till ett regelbundet samklass- r ättlingträd $\mathcal {T}}^{r}(G)}$ { och ${\ displaystyle m-1}$ oregelbundna efterkommande grafer ${\mathcal {T}}^{r+j}(G)$ av samklass $r+j$ , för $1\leq j\leq m-1$ . Följaktligen är det efterkommande trädet för $G$ den disjunkta unionen

$(8)\qquad {\mathcal {T}}(G)={\dot {\cup }}_ {j=0}^{m-1}\,{\mathcal {T}}^{r+j}(G)$ .

Multifurkation är korrelerad med olika ordningar av den sista icke-triviala nedre centralen av omedelbara ättlingar. Eftersom nilpotensklassen ökar exakt med en enhet, $c=\mathrm {cl} (Q)=\mathrm {cl} (P)+1$ , från en förälder $P=Q/\gamma _{c}(Q)=\pi (Q)$ till vilken som helst omedelbar ättling $Q$ , samklassen förblir stabil, ${\displaystyle r=\mathrm {cc} (Q)=\mathrm {cc} (P)} ,$ om den sista icke-triviala nedre central är cyklisk av ordning ${\displaystyle \vert \gamma _{c}(Q)\vert =p} ,$ eftersom ordningens exponent då också ökar exakt med en enhet, $\vert Q\vert =p\cdot \vert P\vert$ . I det här fallet $Q$ en vanlig omedelbar ättling med riktad kant $P\leftarrow Q$ av stegstorlek $1$ , som vanligt. Samklassen ökar dock med $m-1$ , om $\vert \gamma _{c}(Q)\vert =p^{m}$ med $m\geq 2$ . Då kallas ${\displaystyle Q} en$ oregelbunden omedelbar ättling med riktad kant $P\leftarrow Q$ av stegstorlek $m$ .

Om villkoret för stegstorlek $1$ är infört på alla riktade kanter, då är det maximala släktträdet ${\mathcal {T}}(1)$ i trivialgruppen $1$ delar sig i en uträkneligt oändlig osammanhängande förening

$(9)\qquad {\mathcal {T}}(1)={\dot {\cup }}_{r= 0}^{\infty }\,{\mathcal {G}}(p,r)$

av riktade samklassgrafer ${\displaystyle {\mathcal {G}}(p,r)} ,$ som snarare är skogar än träd. Mer exakt antyder de ovan nämnda samklasssatserna det

$(10)\qquad {\mathcal {G}}(p,r)=\ vänster({\dot {\cup }}_{i}\,{\mathcal {T}}(S_{i})\right){\dot {\cup }}{\mathcal {G}}_{0 }(p,r)$

är den disjunkta föreningen av ändligt många samklassträd ${\mathcal {T}}(S_{i})$ av parvisa icke-isomorfa oändliga prop- grupper i $displaystyle S_{i} }$ av samklass $r$ (sats D) och en finit subgraf ${\mathcal {G}}_{0}(p,r)$ av sporadiska grupper som ligger utanför någon samklassträd.

Identifierare

SmallGroups Library- identifierare för ändliga grupper, särskilt av ändliga p -grupper, angivna i formuläret

$\langle \ {\text{order}},\ {\text{counting number}}\ \rangle$

i följande konkreta exempel på ättlingträd, beror på HU Besche, B. Eick och EA O'Brien. När gruppordningarna ges i en skala på vänster sida, som i figur 2 och figur 3, betecknas identifierarna kort med

$\langle \ {\text{räknetal}}\ \rangle$ .

Beroende på primtal $p$ finns det en övre gräns för ordningen av grupper för vilka en SmallGroup-identifierare finns, t.ex. $512=2^{9}$ för ${\ displaystyle p=2}$ och $6561=3^{8}$ för $p=3$ . För grupper av större beställningar används en notation med generaliserade identifierare som liknar den efterkommande strukturen. En vanlig omedelbar ättling, förbunden med en kant av stegstorlek $1$ med dess förälder $P$ , betecknas med

$P-\#1;{\text{räknetal}}$ ,

och en oregelbunden omedelbar ättling, förbunden med en kant av stegstorlek $s\geq 2$ med dess förälder $P$ , betecknas med

$P-\#s;{\text{räknetal}}$ .

Implementeringarna av p -gruppgenereringsalgoritmen i beräkningsalgebrasystemen GAP och Magma använder dessa generaliserade identifierare, som går tillbaka till JA Ascione 1979.

Konkreta exempel på träd

I alla exempel motsvarar den underliggande överordnade definitionen (P2) den vanliga lägre centrala serien. Enstaka skillnader mot den överordnade definitionen (P3) med avseende på den lägre exponent- p centrala serien påpekas.

Samklass 0

Samklassens graf

$(11)\qquad {\mathcal {G}}(p,0)={\mathcal {G}}_{0}(p,0 )$

av ändliga p -grupper av samklass $0$ innehåller inte något samklassträd och består alltså uteslutande av sporadiska grupper, nämligen trivialgruppen $1$ och den cykliska gruppen $C_{p}$ av ordningen $p$ , som är ett löv (dock är det kapabelt med avseende på den lägre exponent- p centralserien). För $p=2$ är SmallGroup -identifieraren för $C_{p}$$\langle 2,1\rangle$ , för $p=3$ det är $\langle 3,1\rangle$ .

Figur 2: Samklassgrafen för ändliga 2-grupper med samklass 1

Samklass 1

Samklassens graf

$(12)\qquad {\mathcal {G}}(p,1)={\mathcal {T} }^{1}(R){\dot {\cup }}{\mathcal {G}}_{0}(p,1)$

av finita p -grupper av samklass $1$ , även kallad för maximal klass , består av det unika samklassträdet ${\mathcal {T}}^{1}(R)$ med rot $R=C_{p}\ gånger C_{p}$ , den elementära abelska p -gruppen av rang $2$ och en enda isolerad vertex (en terminal föräldralös utan korrekt förälder i samma samklassgraf, eftersom den riktade kanten till trivialgruppen $1$ har stegstorlek $2$ ), den cykliska gruppen $C_{p^{2}}$ av ordningen $p^{2}$ i den sporadiska delen ${\mathcal {G}}_{0}(p,1)$ (denna grupp är dock kapabel med avseende på den lägre exponent- p centrala serien). Trädet ${\mathcal {T}}^{1}(R)={\mathcal {T}}^{1}(S_{1})$ är samklassträdet för den unika oändliga prop - gruppen $S_{1}$ av coclass $1$ .

För ${\displaystyle p=2} ,$ resp. $p=3$ , SmallGroup-identifieraren för roten $R$ är ${\displaystyle \langle 4,2\rangle } ,$ resp. $\langle 9,2\rangle$ , och ett träddiagram över samklassgrafen från gren ${\mathcal {B}}(2)$ ner till gren ${\mathcal {B}}(7)$ (räknat med avseende på p -logaritmen av grenrotens ordning) ritas i figur 2, resp. Figur 3, där alla grupper av ordning åtminstone $p^{3}$ är metabelska , det vill säga icke-abelska med härledd längd $2$ (hörn representerade av svarta skivor i motsats till konturrutor som indikerar abelska grupper). I figur 3 betecknar mindre svarta skivor metabelska 3-grupper där även de maximala undergrupperna är icke-abelska, ett särdrag som inte förekommer för de metabelska 2-grupperna i figur 2, eftersom de alla har en abelsk undergrupp av index p $\ displaystyle p}$ (vanligtvis exakt en). Samklassträdet för ${\displaystyle {\mathcal {G}}(2,1)} ,$ resp. ${\mathcal {G}}(3,1)$ , har periodisk rot $\langle 8,3\rangle$ och periodicitet av längd $1$ börjar med gren ${\displaystyle {\mathcal {B}}(3)} ,$ resp. periodisk rot $\langle 81,9\rangle$ och periodicitet för längd $2$ inställning med gren ${\mathcal {B}}(4)$ . Båda träden har grenar med begränsat djup $1$ , så deras virtuella periodicitet är i själva verket en strikt periodicitet .

Samklassträdet för ${\mathcal {G}}(p,1)$ med $p\geq 5$ har dock obegränsat djup och innehåller icke-metabeliska grupper, och samklassträdet för ${\mathcal {G}}(p,1)$ med $p\geq 7$ har jämn obegränsad bredd , det vill säga antalet ättlingar av en fast ordning ökar oändligt med växande ordning.

Med hjälp av kärnor och mål för Artin-överföringar kan diagrammen i figur 2 och figur 3 förses med ytterligare information och ritas om som strukturerade avkommande träd .

De konkreta exemplen ${\mathcal {G}}(2,1)$ och ${\mathcal {G}}(3,1)$ av samklass grafer ger en möjlighet att ge en parametriserad polycyklisk effektkommutatorpresentation för hela samklassträdet $\mathcal {G}}(p,1)}$${\displaystyle {\mathcal {T}}^{1}(R)\subset$ { , $p\in \lbrace 2,3\rbrace$ , som nämns i huvudsektionen som en fördel med konceptet efterträdande träd och som en följd av periodiciteten för hela samklassträdet. I båda fallen genereras en grupp ${\displaystyle G\in {\mathcal {T}}^{1}(R)} av två element$$x,y$ men presentationen innehåller serien av högre kommutatorer $s_{j}=\lbrack s_{j-1},x\rbrack$ , ${\displaystyle 3\leq j\leq n-1=\mathrm {cl} (G)} ,$ som börjar med huvudkommutatorn $s_{2}=\lbrack y,x\rbrack$ . Nilpotensen uttrycks formellt av relationen ${\displaystyle s_{n}=1} ,$ när gruppen är i ordning $\vert G\vert =p^{n}$ .

Figur 3: Samklassgrafen för ändliga 3-grupper med samklass 1

För $p=2$ finns det två parametrar $0\leq w,z\leq 1$ och pc-presentationen ges av

(13) ${\begin{aligned}G^{n} (z,w)=&\langle x,y,s_{2},\ldots ,s_{n-1}\mid \\&x^{2}=s_{n-1}^{w},\ y ^{2}=s_{2}^{-1}s_{n-1}^{z},\ \lbrack s_{2},y\rbrack =1,\\&s_{2}=\lbrack y, x\rbrack ,\ s_{j}=\lbrack s_{j-1},x\rbrack {\text{ for }}3\leq j\leq n-1\rangle \end{aligned}}$

2-grupperna av maximal klass, det vill säga samklass $1$ , bildar tre periodiska oändliga sekvenser ,

• de dihedrala grupperna, $D(2^{n})=G^{n}(0,0)$ , $n\geq 3$ , bildar huvudlinjen (med oändligt kapabla hörn),
• de generaliserade kvaterniongrupperna , $Q(2^{n})=G^{n}(0,1)$ , $n\geq 3$ , som alla är terminala hörn,
• de halvdiedriska grupperna, $S(2^{n})=G^{n}(1,0)$ , $n\geq 4$ , som också är löv.

För $p=3$ finns det tre parametrar $0\leq a\leq 1$ och $-1\leq w,z \leq 1$ och pc-presentationen ges av

(14 ${\ start{aligned}G_{a}^{n}(z,w)=&\langle x,y,s_{2},\ldots ,s_{n-1}\mid \\&x^{3}=s_ {n-1}^{w},\ y^{3}=s_{2}^{-3}s_{3}^{-1}s_{n-1}^{z},\ \lbrack y ,s_{2}\rbrack =s_{n-1}^{a},\\&s_{2}=\lbrack y,x\rbrack ,\ s_{j}=\lbrack s_{j-1},x \rbrack {\text{ för }}3\leq j\leq n-1\rangle \end{aligned}}$

3-grupper med parameter $a=0$ har en abelsk maximal undergrupp, de med parameter $a=1$ har inte det. Närmare bestämt är en befintlig abelsk maximal undergrupp unik, förutom de två extra speciella grupperna $G_{0}^{3}(0,0)$ och $\displaystyle G_{0}^{3}(0,1)}$ , där alla fyra maximala undergrupperna är abelska.

I motsats till någon större samklass ${\displaystyle r\geq 2} innehåller$ samklassgrafen ${\mathcal {G}}(p,1)$ uteslutande p -grupper ${ \displaystyle G}$ med abelianisering $G/G^{\prime }$ av typen $(p,p)$ , förutom dess unika isolerade vertex ${\ displaystil C_{p^{2}}}$ . Fallet $p=2$ kännetecknas av sanningen i det omvända påståendet: Vilken 2-grupp som helst med abelianisering av typen $(2,2)$ är av samklass ${\ displaystyle 1}$ (O. Tausskys sats ).

Figur 4: Gränssnittet mellan ändliga 3-grupper av samklass 1 och 2 av typ (3,3)

Samklass 2

Uppkomsten av samklassgrafen ${\mathcal {G}}(p,r)$ med $r\geq 2$ är inte enhetlig. p -grupper med flera distinkta abelianiseringar bidrar till dess konstitution. För samklass $r=2$ finns det väsentliga bidrag från grupperna $G$ med abelianiseringar $G/G^{\prime }$ av typerna $(p,p)$ , $(p^{2},p)$ , $(p,p,p)$ , och ett isolerat bidrag från den cykliska gruppen $C_{p^{3}}$ av ordningen $p^{3}$ :

$(15)\qquad {\mathcal {G}}(p,2)={\mathcal {G}}_{(p,p)}(p ,2){\dot {\cup }}{\mathcal {G}}_{(p^{2},p)}(p,2){\dot {\cup }}{\mathcal {G}} _{(p,p,p)}(p,2){\dot {\cup }}{\mathcal {G}}_{(p^{3})}(s,2)$ .

Abelianisering av typ ( p , p )

I motsats till p -grupper av samklass $2$ med abelianisering av typ $(p^{2},p)$ eller $(p ) ,p,p)$ , som uppstår som regelbundna ättlingar till abelska p -grupper av samma typer, p -grupper av samklass $2$ med abelianisering av typ $(p,p)$ uppstår från oregelbundna ättlingar till en icke-abelsk p -grupp av coclass $1$ som inte är coclass-settled.

För primtal $p=2$ existerar inte sådana grupper alls, eftersom 2-gruppen $\langle 8,3\rangle$ är samklassfast, vilket är djupare anledning till Tausskys sats. Detta anmärkningsvärda faktum har redan observerats av Giuseppe Bagnera 1898.

För udda primtal ${\displaystyle p\geq 3} beror$ förekomsten av p -grupper av samklass $2$ med abelianisering av typ $(p,p)$ p.g.a. det faktum att gruppen $G_{0}^{3}(0,0)$ inte är samklassbestämd. Dess nukleära rang är lika med $2$ , vilket ger upphov till en bifurkation av ättlingträdet ${\mathcal {T}}(G_{0}^{3}(0 ,0))$ till två samklassgrafer. Den vanliga komponenten ${\mathcal {T}}^{1}(G_{0}^{3}(0,0))$ är ett underträd till det unika trädet ${\mathcal {T}}^{1}(C_{p}\ gånger C_{p})$ i samklassgrafen ${\ mathcal {G}}(s,1)$ . Den oregelbundna komponenten ${\mathcal {T}}^{2}(G_{0}^{3}(0,0))$${\mathcal {G}}={\mathcal {G}}_{(p,p)}(p,2)$ en subgraf i samklassgrafen ${\mathcal {G}}(p,2)$ när anslutningskanterna av stegstorlek $2$ av de oregelbundna omedelbara ättlingarna till $G_{0}^{3 }(0,0)$ tas bort.

För ${\displaystyle p=3} är$ denna subgraf ${\mathcal {G}}$ ritad i figur 4, som visar gränssnittet mellan finita 3-grupper med samklass $1$ och $2$ av typ $(3,3)$ . ${\mathcal {G}}$ har sju toppnivåhörn av tre viktiga slag, alla med ordningen ${\displaystyle 243=3^{5}} ,$ som har upptäckts av G. Bagnera .

• För det första finns det två terminala Schur σ-grupper $\langle 243,5\rangle$ och $\langle 243,7\rangle$ i den sporadiska delen ${\mathcal {G}}_{0}(3,2)$ av samklassgrafen ${\mathcal {G}}(3,2)$ .
• För det andra är de två grupperna $G=\langle 243,4\rangle$ och $G=\langle 243,9\rangle$ rötter till finita träd ${\mathcal {T}}^{2}(G)$ i den sporadiska delen ${\mathcal {G}}_{0}(3 ,2)$ . Men eftersom de inte är samklassfastställda är de kompletta träden ${\mathcal {T}}(G)$ oändliga .
• Slutligen, de tre grupperna $\langle 243,3\rangle$ , $\langle 243,6\rangle$ och ${\24style ,8\rangle }$ ger upphov till (oändliga) samklassträd, t.ex. ${\mathcal {T}}^{2}(\langle 729,40\rangle )$ , ${\mathcal {T}}^{2}(\langle 243,6\rangle )$ , ${\mathcal { T}}^{2}(\langle 243,8\rangle )$ , som var och en har en metabelsk huvudlinje, i samklassgrafen ${\mathcal {G}}(3,2)$ . Ingen av dessa tre grupper är samklassfast.

Genom att visa ytterligare information om kärnor och mål för Artin-överföringar kan vi rita dessa träd som strukturerade efterkommande träd .

Definition. I allmänhet är en Schur-grupp (kallad en sluten grupp av I. Schur, som myntade konceptet) en prop- grupp G $\displaystyle G}$ vars relation rang $d_{2}(G)=\mathrm {dim} _{\mathbb {F} _{p}}(\mathrm {H} ^{2}(G,\mathbb { F} _{p}))$ sammanfaller med dess generatorrang $d_{1}(G)=\mathrm {dim } _{\mathbb {F} _{p}}(\mathrm {H} ^{1}(G,\mathbb {F} _{p}))$ . En σ-grupp är en pro- grupp G $\displaystyle G}$ som har en automorfism $\sigma \in \mathrm {Aut} (G)$ som inducerar inversionen $x\mapsto x^{-1}$ på dess abelianisering $G/G^{\prime }$ . En Schur σ-grupp är en Schur-grupp $G$ som också är en σ-grupp och har en finit abelianisering $G/G^{\prime }$ .

$\langle 243,3\rangle$ är inte roten till ett samklassträd,

eftersom dess omedelbara ättling ${\displaystyle \langle 729,40\rangle } ,$ som är roten till ett samklassträd med metabelska huvudlinjens hörn, har två syskon $\langle 729 rangle$ , resp. $\langle 729,34\rangle$ , som ger upphov till en singel, resp. tre, samklassträd(er) med icke-metabeliska huvudlinjehörn som har cykliska centra av ordningen $3$ och grenar av betydande komplexitet men ändå med begränsat djup $5$ .

Tabell 1: Kvotienter för grupperna G=G(f,g,h)

Parametrar $(f,g,h)$	Abelianization $G/G^{\prime }$	Klass-2-kvot $G/\gamma _{3}(G)$	Klass-3-kvot $G/\gamma _{4}(G)$	Klass-4-kvot $G/\gamma _{5}(G)$
$(0,1,0)$	$(3,3)$	$\langle 27,3\rangle$	$\langle 243,3\rangle$	$\langle 729,40\rangle$
$(0,1,2)$	$(3,3)$	$\langle 27,3\rangle$	$\langle 243,6\rangle$	$\langle 729,49\rangle$
$(1,1,2)$	$(3,3)$	$\langle 27,3\rangle$	$\langle 243,8\rangle$	$\langle 729,54\rangle$
$(1,0,0)$	$(9,3)$	$\langle 81,3\rangle$	$\langle 243,15\rangle$	$\langle 729,79\rangle$
$(0,0,1)$	$(9,3)$	$\langle 81,3\rangle$	$\langle 243,17\rangle$	$\langle 729,84\rangle$
$(0,0,0)$	$(3,3,3)$	$\langle 81,12\rangle$	$\langle 243,53\rangle$	$\langle 729,395\rangle$

Pro-3 grupper av samklass 2 med icke-trivialt centrum

B. Eick, CR Leedham-Green, MF Newman och EA O'Brien har konstruerat en familj av oändliga pro-3 grupper med coclass $2$ som har ett icke-trivialt ordningscentrum $3$ . Familjemedlemmarna kännetecknas av tre parametrar $(f,g,h)$ . Deras ändliga kvotienter genererar alla huvudlinjehörn med bicykliska centra av typen $(3,3)$ av sex samklassträd i samklassgrafen ${\mathcal {G}} (3,2)$ . Associeringen av parametrar till rötterna för dessa sex träd anges i tabell 1, träddiagrammen, förutom abelianiseringen $(3,3,3)$ , visas i figur 4 och Figur 5, och den parametriserade pro-3-presentationen ges av

(16) ${\begin{aligned}G(f,g,h)=&\langle a,t,z\mid \\&a^{ 3}=z^{f},\ \lbrack t,t^{a}\rbrack =z^{g},\ t^{1+a+a^{2}}=z^{h},\ \&z^{3}=1,\ \lbrack z,a\rbrack =1,\ \lbrack z,t\rbrack =1\rangle \end{aligned}}$

Figur 5: Finita 3-grupper av samklass 2 av typ (9,3)

Abelianisering av typ ( p ², p )

För $p=3$ , de översta nivåerna i underträdet ${\mathcal {T}}^{2}(\langle 27,2\rangle )$ i samklassgrafen ${\mathcal {G}}(3,2)$ ritas i figur 5. De viktigaste hörnen i detta träd är de åtta syskonen som delar den gemensamma föräldern ${\displaystyle \langle 81,3\rangle } ,$ som är av tre viktiga slag.

• För det första finns det tre blad $langle 243,20\rangle } ,$$243,16\rangle }$ ⟨ $\displaystyle \langle 243,19\rangle$$}$ , med cykliskt ordningscentrum $9$ och ett enda blad $\langle 243,18\rangle$ med bicykliskt centrum av typen ${\ displaystil (3,3)}$ .
• För det andra är gruppen $G=\langle 243,14\rangle$ roten till ett ändligt träd ${\mathcal {T}} (G)={\mathcal {T}}^{2}(G)$ .
• Slutligen, de tre grupperna ${\displaystyle \langle 243,13\rangle } ,$ ⟨ $\langle 243,15\rangle }$$displaystyle$ och $,17\rangle }$ ger upphov till oändliga samklassträd, t.ex. ${\mathcal {T}}^{2}(\langle 2187,319\rangle )$ , ${\mathcal {T}}^{2}(\langle 243,15\rangle )$ , ${\mathcal {T} }^{2}(\langle 243,17\rangle )$ , var och en med en metabelsk huvudlinje, den första med cykliska centra av ordningen $3$ , den andra och tredje med bicykliska centra av typen $(3,3)$ .

Här är $\langle 243,13\rangle$ inte roten till ett samklassträd, eftersom förutom dess avkomling $\langle 2187,319,\rangle$ roten till ett samklassträd med metabelska huvudlinjepunkten, den har ytterligare fem avkomlingar som ger upphov till samklassträd med icke-metabelska huvudlinjepunkten med cykliska centra av ordningen 3 {\ $3}$ och grenar av extrem komplexitet, här delvis även med obegränsat djup .

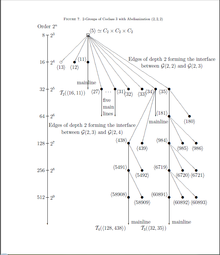
Figur 6: Finita 2-grupper av samklass 2,3,4 och typ (2,2,2)

Abelianisering av typ ( p , p , p )

För ${\displaystyle p=2} ,$ resp. $p=3$ , det finns ett unikt samklassträd med p -grupper av typen $(p,p,p)$ i samklassgrafen ${\mathcal {G}}(s,2)$ . Dess rot är den elementära abelska p -gruppen av typen $(p,p,p)$ , det vill säga $\langle 8,5\rangle$ , resp. $\langle 27,5\rangle$ . Detta unika träd motsvarar pro-2-gruppen i familjen $\#59$ av MF Newman och EA O'Brien, resp. till pro-3-gruppen som ges av parametrarna $(f,g,h)=(0,0,0)$ i tabell 1. För ${ \displaystyle p=2}$ , trädet indikeras i figur 6, som visar några ändliga 2-grupper med coclass $2,3,4$ av typen $(2,2,2)$ .

Samklass 3

Även här bidrar p -grupper med flera distinkta abelianiseringar till konstitutionen av samklassgrafen ${\mathcal {G}}(p,3)$ . Det finns regelbundna, resp. oregelbundna, väsentliga bidrag från grupperna $G$ med abelianiseringar $G/G^{\prime }$ av typerna $(p^{3},p )$ , $(p^{2},p^{2})$ , $(p^{2},p,p)$ , $(p,p,p,p)$ , resp. $(p,p)$ , $(p^{2},p)$ , $(p,p, p)$ , och ett isolerat bidrag från den cykliska gruppen $C_{p^{4}}$ av ordningen $p^{4}$ .

Abelianisering av typ ( p , p , p )

Eftersom den elementära abelska p -gruppen $C_{p}\times C_{p}\times C_{p}$ av rang $3$ , det vill säga $\langle 8,5\rangle$ , resp. $\langle 27,5\rangle$ , för $p=2$ , resp. $p=3$ , är inte samklassbestämd, det ger upphov till en multifurkation. Den vanliga komponenten ${\displaystyle {\mathcal {T}}^{2}(C_{p}\times C_{p}\times C_{p})} har$ varit beskrivs i avsnittet om coclass $2$ . Den oregelbundna komponenten ${\displaystyle {\mathcal {T}}^{3}(C_{p}\times C_{p}\times C_{p})} blir$ en subgraf ${\mathcal {G}}={\mathcal {G}}_{(p,p,p)}(p,3)$ av samklassgrafen ${\mathcal {G}}(p,3)$ när anslutningskanterna av stegstorlek $2$ av de oregelbundna omedelbara avkomlingarna av $C_{p}\times C_{p}\times C_{p}$ tas bort.

För ${\displaystyle p=2} finns$ denna subgraf ${\mathcal {G}}$ i figur 6. Den har nio toppnivåer av ordningen $32=2 ^{5}$ som kan delas in i terminala och kapabla hörn.

• De två grupperna $\langle 32,32\rangle$ och $\langle 32,33\rangle$ är löv.
• De fem grupperna $\langle 32,27..31\rangle$ och de två grupperna $\langle 32,34..35\rangle$ är oändligt kapabla.

Träden som härrör från de kapabla hörnen associeras med oändliga pro-2-grupper av MF Newman och EA O'Brien på följande sätt.

$\langle 32,28\rangle$ ger upphov till två träd,

${\mathcal {T}}^{3}(\langle 64,140\rangle )$ associerad med familj $\#73$ , och

${\mathcal {T}}^{3}(\langle 64,147\rangle )$ associerad med familj $\#74$ .

${\mathcal {T}}^{3}(\langle 32,29\rangle )$ är associerad med familj $\#75$ .

${\mathcal {T}}^{3}(\langle 32,30\rangle )$ är associerad med familj $\#76$ .

${\mathcal {T}}^{3}(\langle 32,31\rangle )$ är associerad med familj $\#77$ .

$\langle 32,34\rangle$ ger upphov till

${\mathcal {T}}^{3}(\langle 64,174\rangle )$ associerad med familj $\#78$ . Till sist,

${\mathcal {T}}^{3}(\langle 32,35\rangle )$ är associerad med familj $\#79$ .

Tabell 2: Klass-2-kvoter Q av vissa metabelska 2-grupper G av typ (2,2,2)

SmallGroups identifierare för Q	Hall Senior klassificering av Q	Schur multiplikator ${\mathcal {M}}(Q)$	2-rank av G' $r_{2}(G^{\prime })$	4-rank av G' $r_{4}(G^{\prime })$	Maximalt $r_{2}(H_{i}/H_{i}^{\prime })$
$\langle 32,32\rangle$	32.040	$(2)$	$2$	$0$	$2$
$\langle 32,33\rangle$	32.041	$(2)$	$2$	$0$	$2$
$\langle 32,29\rangle$	32,037	$(2,2)$	$2$	$1$	$3$
$\langle 32,30\rangle$	32,038	$(2,2)$	$2$	$1$	$3$
$\langle 32,35\rangle$	32,035	$(2,2)$	$2$	$1$	$3$
$\langle 32,28\rangle$	32,036	$(2,2,2)$	$2$	$2$	$3$
$\langle 32,27\rangle$	32.033	$(2,2,2,2)$	$3$	$2$ eller $3$	$4$

Hall-Senior klassificering av 2-grupper

$Q=G/\gamma _{3}(G)$ nio toppnivåhörn har undersökts av E. Benjamin, F. Lemmermeyer och C. Snyder med avseende på deras förekomst som klass-2-kvotienter av större metabelska 2-grupper $G$ av typen $(2,2,2)$ och med samklass $3$ , som är exakt medlemmarna av de sju hörnens ättlingträd. Dessa författare använder klassificeringen av 2-grupper av M. Hall och JK Senior som sätts i överensstämmelse med SmallGroups Library i tabell 2. Komplexiteten hos de efterkommande träden för dessa sju hörn ökar med de 2- och 4-graderna indikerade i tabell 2, där de maximala undergrupperna av index $2$ i $G$ betecknas med $H_{i}$ , för $1\leq i \leq 7$ .

Historia

Ättlingträd med centrala kvoter som föräldrar (P1) är implicita i P. Halls skrift från 1940 om isoklinism av grupper. Träd med sista icke-triviala lägre centrala kvoter som föräldrar (P2) presenterades först av CR Leedham-Green vid International Congress of Mathematicians i Vancouver, 1974. De första omfattande träddiagrammen har ritats manuellt av JA Ascione, G. Havas och CR Leedham-Green (1977), av JA Ascione (1979) och av B. Nebelung (1989). antogs föräldradefinitionen med hjälp av den lägre exponent- p centralserien (P3) med tanke på beräkningsfördelar, i det senare fallet, där teoretiska aspekter fokuserades, togs föräldrarna med avseende på det vanliga nedre centrala serien (P2).

Se även

• Kärnorna och målen för Artin-överföringar har nyligen visat sig vara kompatibla med förälder-ättling-relationer mellan ändliga p -grupper och kan med fördel användas för att ge efterkommande träd ytterligare struktur.