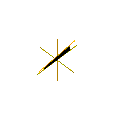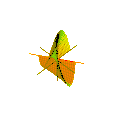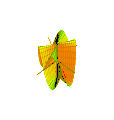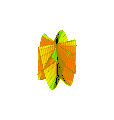Plückers konoid

Figur 1. Plückers konoid med n = 2 .

Figur 2. Plückers konoid med n = 3 .

Figur 3. Plückers konoid med n = 4 .

Inom geometrin är Plückers konoid en styrd yta uppkallad efter den tyske matematikern Julius Plücker . Det kallas också en konisk kil eller cylindroid ; dock är det senare namnet tvetydigt, eftersom "cylindroid" också kan hänvisa till en elliptisk cylinder .

Plückers konoid är ytan som definieras av funktionen av två variabler:

$z={\frac {2xy}{x^{2}+y^{2}}}.$

Denna funktion har en väsentlig singularitet vid ursprunget .

Genom att använda cylindriska koordinater i rymden kan vi skriva in ovanstående funktion i parametriska ekvationer

$x=v\cos u,\quad y=v\sin u,\quad z=\sin 2u.$

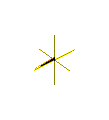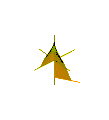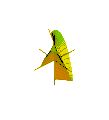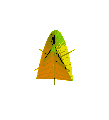
Plückers konoid är alltså en höger konoid , vilket kan erhållas genom att rotera en horisontell linje kring z -axeln med den oscillerande rörelsen (med period 2 π ) längs segmentet [–1, 1] av axeln (Figur 4).

En generalisering av Plückers konoid ges av de parametriska ekvationerna

$x=v\cos u,\quad y=v\sin u,\quad z=\sin nu.$

där n anger antalet veck i ytan. Skillnaden är att perioden för den oscillerande rörelsen längs z -axeln är 2π / n . (Figur 5 för n = 3 )

Figur 4. Plückers konoid med n = 2 .

Figur 5. Plückers konoid med n = 3

• 

  Animation av Pluckers konoid med n = 2

• 

  Plockarens konoid med n = 2

• 

  Plockarens konoid med n = 3

• 

  Animation av Pluckers konoid med n = 2

• 

  Animation av Pluckers konoid med n = 3

• 

  Plockarens konoid med n = 4

Se även

• Regerad yta
• Höger konoid

•   A. Gray, E. Abbena, S. Salamon, Modern differentialgeometri av kurvor och ytor med Mathematica, 3:e uppl. Boca Raton, Florida:CRC Press, 2006. [1] ( ISBN 978-1-58488-448-4 )
•   Vladimir Y. Rovenskii, Geometri av kurvor och ytor med LÖNN [2] ( ISBN 978-0-8176-4074-3 )

externa länkar

• Weisstein, Eric W. "Plückers Conoid" . MathWorld .