Whitney paraply

Sektion av ytan

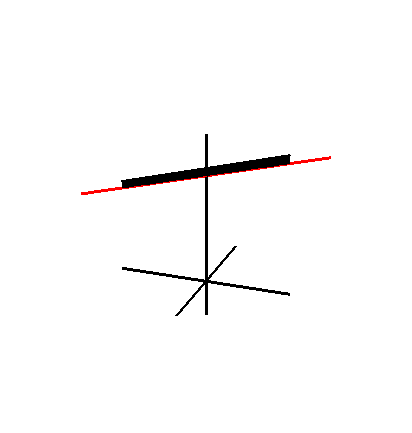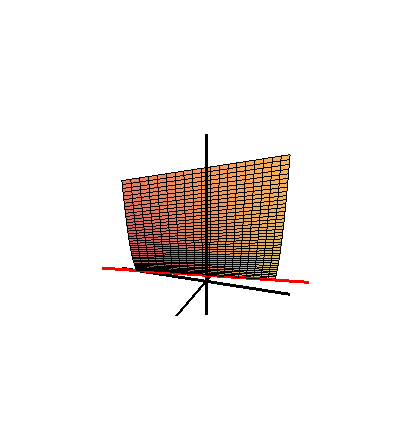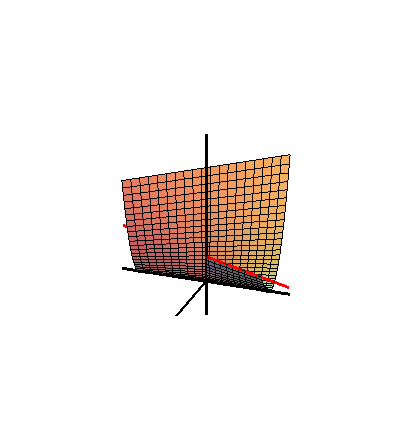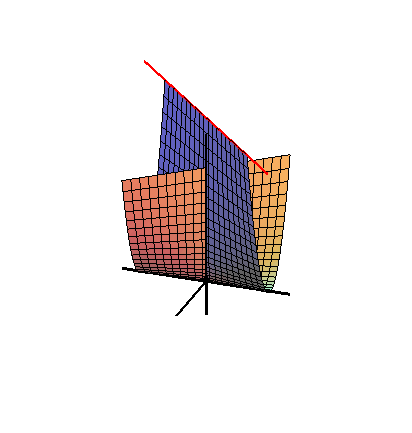
Inom geometri är Whitney -paraplyet (eller Whitneys paraply , uppkallat efter den amerikanske matematikern Hassler Whitney , och ibland kallat ett Cayley-paraply ) en specifik självskärande styrd yta placerad i tre dimensioner . Det är föreningen av alla räta linjer som passerar genom punkter i en fix parabel och är vinkelräta mot en fixerad rät linje som är parallell med parabelns axel och ligger på dess vinkelräta halveringsplan .

Formler

Whitneys paraply kan ges av de parametriska ekvationerna i kartesiska koordinater

$\left\{{\begin{aligned}x(u,v)& =uv,\\y(u,v)&=u,\\z(u,v)&=v^{2},\end{aligned}}\right.$

där parametrarna u och v sträcker sig över de reella talen . Det ges också av den implicita ekvationen

$x^{2}-y^{2}z=0.$

Denna formel inkluderar också den negativa z -axeln (som kallas handtaget på paraplyet).

Egenskaper

Whitney paraply som en rät yta, genererad av en rörlig rak linje

Whitney paraply gjort med en enda sträng inuti en plastkub

Whitneys paraply är en regerad yta och en höger konoid . Det är viktigt inom singularitetsteorin , som en enkel lokal modell av en pinch point singularitet . Nyppunkten och viksingulariteten är de enda stabila lokala singulariteterna för kartor från R ² till R ³ .

Den är uppkallad efter den amerikanske matematikern Hassler Whitney .

I strängteorin är en Whitney-bran en D7-bran som omsluter en sort vars singulariteter är lokalt modellerade av Whitney-paraplyet. Whitney branes dyker upp naturligt när man tar Sens svaga kopplingsgräns för F-teori .

Se även

• Korsmössa
• Höger konoid
• Regerad yta

• "Whitneys paraply" . Den topologiska djurparken . Geometricentret . Hämtad 2006-03-08 . (Bilder och filmer av Whitney-paraplyet.)